Câu hỏi:
Cho góc α = 120°. Trong các khẳng định sau, khẳng định nào là SAI?
A. \(\sin 120^\circ = \frac{{\sqrt 3 }}{2}\);
B. \(\cos 120^\circ = – \frac{1}{2}\);
C. \(\tan 120^\circ = – \sqrt 3 \);
D. \(\cot 120^\circ = \sqrt 3 \).
Đáp án chính xác
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có sin120° = sin(180° – 60°) = sin60°\( = \frac{{\sqrt 3 }}{2}\).
cos120° = cos(180° – 60° ) = – cos60° \( = – \frac{1}{2}\).
Do đó \(\tan 120^\circ = \frac{{\sin 120^\circ }}{{\cos 120^\circ }} = – \sqrt 3 \);
\(\cot 120^\circ = – \frac{1}{{\sqrt 3 }}\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tìm các giá trị lượng giác của góc 120°.
Câu hỏi:
Tìm các giá trị lượng giác của góc 120°.
Trả lời:
Hướng dẫn giải:
Lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = 120^\circ \).
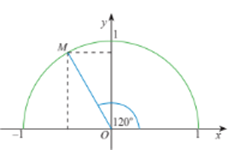 Ta có: \(\widehat {MOy} = 120^\circ – 90^\circ = 30^\circ \).
Ta có: \(\widehat {MOy} = 120^\circ – 90^\circ = 30^\circ \).
Ta tính được tọa độ điểm M: \(\left\{ \begin{array}{l}{x_0} = – \left( {OM.\sin 30^\circ } \right) = – \left( {1.\frac{1}{2}} \right) = – \frac{1}{2}\\{y_0} = OM.\cos 30^\circ = 1.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{2}\end{array} \right.\).
Hay \(M\left( { – \frac{1}{2};\,\,\frac{{\sqrt 3 }}{2}} \right)\).
Vậy theo định nghĩa ta có:
\(\sin 120^\circ = \frac{{\sqrt 3 }}{2};\,\cos 120^\circ = – \frac{1}{2}\); \(\tan 120^\circ = – \sqrt 3 ;\,\cot 120^\circ = – \frac{{\sqrt 3 }}{3}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho góc α = 135°. Hãy tính sinα, cosα, tanα và cotα.
Câu hỏi:
Cho góc α = 135°. Hãy tính sinα, cosα, tanα và cotα.
Trả lời:
Hướng dẫn giải:
Ta có sin135° = sin(180° – 45°) = sin45° = \(\frac{{\sqrt 2 }}{2}\);
cos135° = cos(180° – 45°) = – cos45° = \( – \frac{{\sqrt 2 }}{2}\);
\(\tan 135^\circ = \frac{{\sin 135^\circ }}{{\cos 135^\circ }} = \frac{{\frac{{\sqrt 2 }}{2}}}{{ – \frac{{\sqrt 2 }}{2}}} = – 1\).
Do đó cot135° = \(\frac{{cos135^\circ }}{{\sin 135^\circ }} = \frac{{ – \frac{{\sqrt 2 }}{2}}}{{\frac{{\sqrt 2 }}{2}}} = – 1\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác cân DEF có \(\widehat D = \widehat E = 15^\circ \). Hãy tính các giá trị lượng giác của góc F.
Câu hỏi:
Cho tam giác cân DEF có \(\widehat D = \widehat E = 15^\circ \). Hãy tính các giá trị lượng giác của góc F.
Trả lời:
Hướng dẫn giải:
Ta có \(\widehat F = 180^\circ – \left( {\widehat D + \widehat E} \right) = 180^\circ – 30^\circ = 150^\circ \).
Do đó sinF = sin150° = sin(180° − 30°) = sin30° = \(\frac{1}{2}\);
cosF = cos150° = cos(180° − 30°)= − cos30° = \( – \frac{{\sqrt 3 }}{2}\);
tanF = \(\frac{{\sin 150^\circ }}{{\cos 150^\circ }} = \frac{{\frac{1}{2}}}{{ – \frac{{\sqrt 3 }}{2}}} = – \frac{{\sqrt 3 }}{3}\);
cotF = \(\frac{{cos150^\circ }}{{\sin 150^\circ }} = \frac{{ – \frac{{\sqrt 3 }}{2}}}{{\frac{1}{2}}}\)= \( – \sqrt 3 \).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong các đẳng thức sau đây, đẳng thức nào đúng?
Câu hỏi:
Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sin60° = \(\frac{{\sqrt 3 }}{2}\);
Đáp án chính xác
B. cos60° = \(\frac{{\sqrt 3 }}{2}\);
C. tan60° = 1;
D. cot60° = −1.
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có sin60° = \(\frac{{\sqrt 3 }}{2}\); cos60° = \(\frac{1}{2}\); tan60° =\(\sqrt 3 \); cot60° =\(\frac{1}{{\sqrt 3 }}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Giá trị của tan135° bằng:
Câu hỏi:
Giá trị của tan135° bằng:
A. 1;
B. –1;
Đáp án chính xác
C. \(\frac{1}{2}\);
D. \( – \frac{1}{2}\).
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có: tan135° = – tan(180° – 45°) = – 1.====== **** mời các bạn xem câu tiếp bên dưới **** =====