Cho bốn điểm phân biệt A, B, C, D. Điều kiện nào trong các đáp án A, B, C, D sau đây là điều kiện cần và đủ để AB→=CD→ ?

Câu hỏi:

Cho bốn điểm phân biệt A, B, C, D. Điều kiện nào trong các đáp án A, B, C, D sau đây là điều kiện cần và đủ để $\overrightarrow{AB}=\overrightarrow{CD}$ ?

A. ABCD là hình bình hành.  

Đáp án chính xác

B. ABCD là hình tứ giác

C. AC = BD

D. AB = CD

Trả lời:

Đáp án đúng là : A

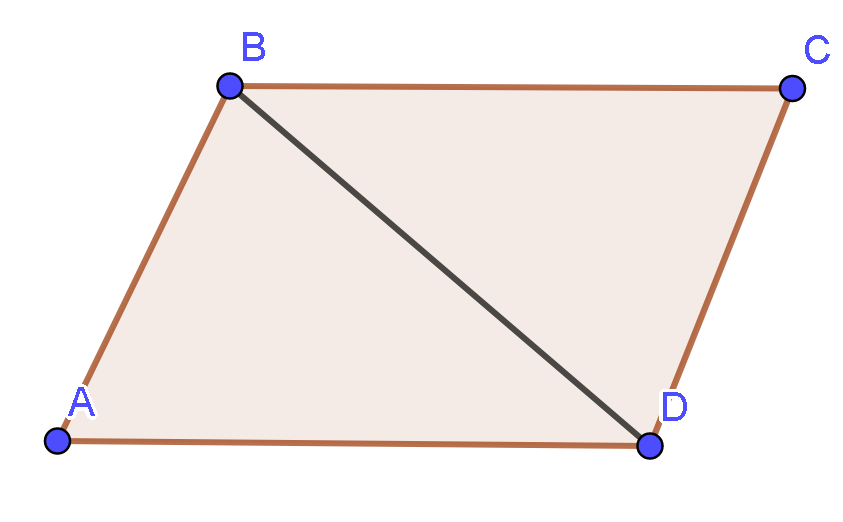
Ta có:
 $\overrightarrow{AB}=\overrightarrow{CD}\Rightarrow \left\{\begin{array}{l}AB\parallel CD\\ AB=CD\end{array}\right.\Rightarrow ABDC$ là hình bình hành.
 Mặt khác, ABCD là hình bình hành $\Rightarrow \left\{\begin{array}{l}AB\parallel CD\\ AB=CD\end{array}\right.$  và $\overrightarrow{AB};\overrightarrow{DC}$  cùng hướng $\Rightarrow \overrightarrow{AB}=\overrightarrow{CD}$ .
Do đó, điều kiện cần và đủ để $\overrightarrow{AB}=\overrightarrow{CD}$  là ABCD là hình bình hành.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tam giác ABC có AB=5, BC=7, CA=8 . Số đo góc A^  bằng:
   
   

   Câu hỏi:
   

   Tam giác ABC có $AB=5,BC=7,CA=8$ . Số đo góc $\widehat{A}$  bằng:

   A. $30°;$

   B. $45°;$

   C. $60°;$

   Đáp án chính xác

   D. $90°;$

   Trả lời:

   Đáp án đúng là: C
   Theo định lí hàm cosin, ta có: $\cos \widehat{A}=\frac{A{B}^2+A{C}^2-B{C}^2}{2AB.AC}=\frac{5^2+8^2-7^2}{\mathrm{2.5.8}}=\frac{1}{2}$ .
   Do đó,$\widehat{A}=60°$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tam giác ABC có AC=4, BAC^=30°, ACB^=75° . Tính diện tích tam giác ABC.
   
   

   Câu hỏi:
   

   Tam giác ABC có $AC=4,\widehat{BAC}=30°,\widehat{ACB}=75°$ . Tính diện tích tam giác ABC.

   A. $S_{\Delta ABC}=8$

   B. $S_{\Delta ABC}=4\sqrt{3}$

   C. $S_{\Delta ABC}=4$

   Đáp án chính xác

   D. $S_{\Delta ABC}=8\sqrt{3}$

   Trả lời:

   Đáp án đúng là: C
   Ta có: $\widehat{ABC}={180}^0-\left(\widehat{BAC}+\widehat{ACB}\right)=75°=\widehat{ACB}\text{.}$
   Suy ra tam giác ABC cân tại A nên $AB=AC=4$
   Diện tích tam giác ABC là $S_{\Delta ABC}=\frac{1}{2}AB.AC\sin \widehat{BAC}=4$  (đơn vị diện tích)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tam giác ABC, có bao nhiêu vectơ khác vectơ – không, có điểm đầu và điểm cuối là các đỉnh A, B, C.
   
   

   Câu hỏi:
   

   Cho tam giác ABC, có bao nhiêu vectơ khác vectơ – không, có điểm đầu và điểm cuối là các đỉnh A, B, C.

   A. 3

   B. 6

   Đáp án chính xác

   C. 4

   D. 9

   Trả lời:

   Đáp án đúng là: B
   Đó là các vectơ: $\overrightarrow{AB},\overrightarrow{BA},\overrightarrow{BC},\overrightarrow{CB},\overrightarrow{CA},\overrightarrow{AC}.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
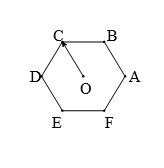
4. Cho lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ – không, cùng phương với OC→ có điểm đầu và điểm cuối là các đỉnh của lục giác là
   
   

   Câu hỏi:
   

   Cho lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ – không, cùng phương với $\overrightarrow{OC}$ có điểm đầu và điểm cuối là các đỉnh của lục giác là

   A. 4

   B. 6

   Đáp án chính xác

   C. 7

   D. 9

   Trả lời:

   Đáp án đúng là: B
   Đó là các vectơ: $\overrightarrow{AB},\overrightarrow{BA},\overrightarrow{DE},\overrightarrow{ED},\overrightarrow{FC},\overrightarrow{CF}$ .
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tam giác ABC có AB=2, AC=3 và C^=45° . Tính độ dài cạnh BC.
   
   

   Câu hỏi:
   

   Tam giác ABC có $AB=\sqrt{2},AC=\sqrt{3}$ và $\widehat{C}=45°$ . Tính độ dài cạnh BC.

   A. $BC=\sqrt{5};$

   B. $BC=\frac{\sqrt{6}+\sqrt{2}}{2};$

   Đáp án chính xác

   C. $BC=\frac{\sqrt{6}–\sqrt{2}}{2};$

   D. $BC=\sqrt{6};$

   Trả lời:

   Đáp án đúng là: B
   Theo định lí hàm cosin, ta có:
   $A{B}^2=A{C}^2+B{C}^2-2.AC.BC.\cos \widehat{C}$
   $\Rightarrow {\left(\sqrt{2}\right)}^2={\left(\sqrt{3}\right)}^2+B{C}^2-2.\sqrt{3}.BC.\cos 45°$

   – $\Rightarrow B{C}^2–\sqrt{6}$.BC + 1 = 0
   $\Rightarrow BC=\frac{\sqrt{6}+\sqrt{2}}{2}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====