Cho ba vectơ a→, b→, c→ đều khác vectơ . Các khẳng định sau đúng hay sai? a) Nếu hai vectơ a→, b→ cùng phương với c→ thì a→ và b→ cùng phương. b) Nếu hai vectơ a→, b→ cùng ngược hướng với c→thì a→ và b→ cùng hướng

Câu hỏi:

Cho ba vectơ $\vec{a}, \vec{b}, \vec{c}$ đều khác vectơ . Các khẳng định sau đúng hay sai?
a) Nếu hai vectơ $\vec{a}, \vec{b}$ cùng phương với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ cùng phương.
b) Nếu hai vectơ $\vec{a}, \vec{b}$ cùng ngược hướng với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ cùng hướng

Trả lời:

a) Gọi Δ₁, Δ₂, Δ₃ lần lượt là giá của ba vectơ $\vec{a}, \vec{b}, \vec{c}$ .
+ Vectơ $\vec{a}$ cùng phương với vectơ $\vec{c}$
⇒ Δ₁ //≡ Δ₃
+ Vectơ $\vec{b}$ cùng phương với vectơ $\vec{c}$
⇒ Δ₂ //≡ Δ₃
Do đó: Δ₁ //≡ Δ₂
Vậy vectơ $\vec{a}$ cùng phương với vectơ $\vec{b}$ (theo định nghĩa).
Vậy khẳng định a) đúng.
b) Hai vectơ $\vec{a}, \vec{b}$ cùng ngược hướng với $\vec{c}$ .
Suy ra $\vec{a}, \vec{b}$ đều cùng phương với $\vec{c}$ .
Theo câu a suy ra vectơ $\vec{a}$ cùng phương với vectơ $\vec{b}$ .
Do đó, hai vectơ $\vec{a}$ và $\vec{b}$ chỉ có thể cùng hướng hoặc ngược hướng.
Mà hai vectơ $\vec{a}$ và $\vec{b}$ đều ngược hướng với $\vec{c}$ nên hai vectơ $\vec{a}$ và $\vec{b}$ cùng hướng.
Vậy khẳng định b) đúng.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo và AB = a, BC = 3a. a) Tính độ dài của các vectơ AC→, BD→ . b) Tìm trong hình các cặp vectơ đối nhau và có độ dài bằng a102 .

Câu hỏi:

Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo và AB = a, BC = 3a.
a) Tính độ dài của các vectơ $\vec{A C}, \vec{B D}$ .
b) Tìm trong hình các cặp vectơ đối nhau và có độ dài bằng $\frac{a \sqrt{10}}{2}$ .

Trả lời:

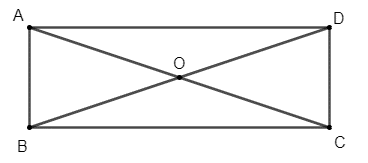
a) Vì ABCD là hình chữ nhật nên hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm O.
Xét tam giác ABC vuông tại B, theo định lí Pythagore ta có:
AC² = AB² + BC² = a² + (3a)² = 10a² $\Rightarrow A C = a \sqrt{10}$ .
Do đó: BD = AC = $a \sqrt{10}$ .
Vậy $| \vec{A C} | = A C = a \sqrt{10}, | \vec{B D} | = B D = a \sqrt{10}$ .
b) Vì O là trung điểm của AC nên AO = OC = $\frac{1}{2}$ AC = $\frac{a \sqrt{10}}{2}$ .
Khi đó: $| \vec{A O} | = | \vec{O A} | = | \vec{O C} | = | \vec{C O} | = \frac{a \sqrt{10}}{2}$
Hai vectơ $\vec{O A}$ và $\vec{O C}$ ngược hướng và có độ dài bằng nhau nên hai vectơ này đối nhau.
Hai vectơ $\vec{A O}$ và $\vec{C O}$ ngược hướng và có độ dài bằng nhau nên hai vectơ này đối nhau.
Vì O là trung điểm của BD nên BO = OD = $\frac{1}{2}$ BD = $\frac{a \sqrt{10}}{2}$ .
Khi đó: $| \vec{B O} | = | \vec{O B} | = | \vec{O D} | = | \vec{D O} | = \frac{a \sqrt{10}}{2}$ .
Hai vectơ $\vec{O B}$ và $\vec{O D}$ ngược hướng và có độ dài bằng nhau nên hai vectơ này đối nhau.
Hai vectơ $\vec{B O}$ và $\vec{D O}$ ngược hướng và có độ dài bằng nhau nên hai vectơ này đối nhau.
Vậy các cặp vectơ đối nhau và có độ dài bằng $\frac{a \sqrt{10}}{2}$ trong hình là: $\vec{O A}, \vec{O C}$ ; $\vec{A O}, \vec{C O}$ ; $\vec{O B}, \vec{O D}$ và $\vec{B O}, \vec{D O}$ .

====== **** mời các bạn xem câu tiếp bên dưới **** =====
Cho hình thoi ABCD có cạnh bằng a và có góc A bằng 60°. Tìm độ dài các vectơ sau: p→=AB→+AD→; u→=AB→−AD→ ;v→=2AB→−AC→ .

Câu hỏi:

Cho hình thoi ABCD có cạnh bằng a và có góc A bằng 60°. Tìm độ dài các vectơ sau: $\vec{p} = \vec{A B} + \vec{A D}$ ; $\vec{u} = \vec{A B} - \vec{A D}$ ; $\vec{v} = 2 \vec{A B} - \vec{A C}$ .

Trả lời:

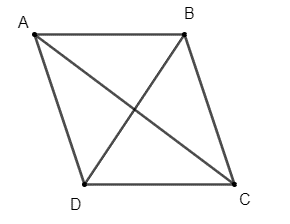
ABCD là hình thoi nên AB = BC = CD = DA = a.
Xét tam giác ABD có AB = AD và $\hat{B A D} = 60 °$ nên tam giác ABD đều.
Suy ra BD = AB = AD = a.
Ta có: $\hat{A D C} = 180 ° - \hat{B A D} = 180 ° - 60 ° = 120 °$ .
Áp dụng định lí côsin trong tam giác ADC ta có:
AC² = AD² + DC² – 2 . AD . DC . cosADC
= a² + a² – 2 . a . a . cos120° = 3a²
Suy ra: AC = $a \sqrt{3}$ .
+ Vì ABCD là hình thoi nên ABCD cũng là hình bình hành nên theo quy tắc hình bình hành ta có: $\vec{p} = \vec{A B} + \vec{A D} = \vec{A C}$ .
Do đó: $| \vec{p} | = | \vec{A C} | = A C = a \sqrt{3}$ .
+ Ta có: $\vec{u} = \vec{A B} - \vec{A D} = \vec{D B}$
Do đó: $| \vec{u} | = | \vec{D B} | = D B = a$ .
+ Ta có: $\vec{v} = 2 \vec{A B} - \vec{A C} = 2 \vec{A B} - (\vec{A B} + \vec{A D})$ $= \vec{A B} - \vec{A D} = \vec{D B}$
Do đó: $| \vec{v} | = | \vec{D B} | = D B = a$ .

====== **** mời các bạn xem câu tiếp bên dưới **** =====
Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E sao cho CE→=AN→ (Hình 1). a) Tìm tổng của các vectơ NC→ và MC→ ; AM→ và CD→ ; AD→ và NC→ . b) Tìm các vectơ hiệu: NC→−MC→; AC→−BC→; AB→−ME→ . c) Chứng minh AM→+AN→=AB→+AD→ .

Câu hỏi:

Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E sao cho $\vec{C E} = \vec{A N}$ (Hình 1).

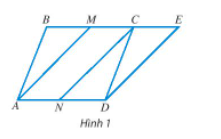
a) Tìm tổng của các vectơ $\vec{N C}$ và $\vec{M C}$ ; $\vec{A M}$ và $\vec{C D}$ ; $\vec{A D}$ và $\vec{N C}$ .
b) Tìm các vectơ hiệu: $\vec{N C} - \vec{M C}; \vec{A C} - \vec{B C}; \vec{A B} - \vec{M E}$ .
c) Chứng minh $\vec{A M} + \vec{A N} = \vec{A B} + \vec{A D}$ .

Trả lời:

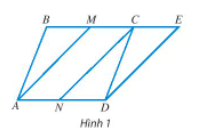
a) Vì ABCD là hình bình hành nên BC // = AD.
M và N lần lượt là trung điểm của BC và AD nên BM = MC = $\frac{1}{2}$ BC; AN = ND = $\frac{1}{2}$ AD
Mà $\vec{C E} = \vec{A N}$ nên CE //= AN.
Do đó: BM = MC = AN = ND = CE (1).
Hai vectơ $\vec{A N}$ và $\vec{M C}$ cùng hướng (do AN // MC và cùng hướng đi từ trái qua phải) và $| \vec{M C} | = | \vec{A N} |$ nên $\vec{A N} = \vec{M C}$ .
Khi đó ta có AMCN là hình bình hành nên $\vec{A M} = \vec{N C}$ .
Do đó: $\vec{N C} + \vec{M C} = \vec{A M} + \vec{M C} = \vec{A C}$
$\vec{A M} + \vec{C D} = \vec{N C} + \vec{C D} = \vec{N D}$

Lại có: ME = MC + CE; AD = AN + ND (2)
Từ (1) và (2) suy ra ME = AD, mà ME // AD nên AMED là hình bình hành, theo quy tắc hình bình hành ta có: $\vec{A M} + \vec{A D} = \vec{A E}$ .
Do đó ta có: $\vec{A D} + \vec{N C} = \vec{A D} + \vec{A M} = \vec{A E}$ .
b) Vì $\vec{A M} = \vec{N C}$ và $\vec{M C} = \vec{A N}$ nên $\vec{N C} - \vec{M C} = \vec{A M} - \vec{A N} = \vec{N M}$ .
Vì ABCD là hình bình hành nên $\vec{B C} = \vec{A D}$ và $\vec{A B} = \vec{D C}$ .
Do đó ta có: $\vec{A C} - \vec{B C} = \vec{A C} - \vec{A D} = \vec{D C} = \vec{A B}$ .
Vì AMED là hình bình hành nên $\vec{M E} = \vec{A D}$ .
Do đó ta có: $\vec{A B} - \vec{M E} = \vec{A B} - \vec{A D} = \vec{D B}$ .
c) Do ABCD là hình bình hành nên $\vec{A C} = \vec{A B} + \vec{A D}$ .
Do AMCN là hình bình hành nên $\vec{A C} = \vec{A M} + \vec{A N}$ .
Từ đó suy ra: $\vec{A M} + \vec{A N} = \vec{A B} + \vec{A D}$ .

====== **** mời các bạn xem câu tiếp bên dưới **** =====
Cho a→ , b→ là hai vectơ khác vectơ 0→ . Trong trường hợp nào thì đẳng thức sau đúng? a) |a→+b→|=|a→|+|b→| ; b) |a→+b→|=|a→−b→| .

Câu hỏi:

Cho $\vec{a}$ , $\vec{b}$ là hai vectơ khác vectơ $\vec{0}$ . Trong trường hợp nào thì đẳng thức sau đúng?
a) $| \vec{a} + \vec{b} | = | \vec{a} | + | \vec{b} |$ ;
b) $| \vec{a} + \vec{b} | = | \vec{a} - \vec{b} |$ .

Trả lời:

a) Áp dụng công thức ${\vec{u}}^{2} = {| \vec{u} |}^{2}$ .
Bình phương hai vế của đẳng phức $| \vec{a} + \vec{b} | = | \vec{a} | + | \vec{b} |$ , ta được: ${| \vec{a} + \vec{b} |}^{2} = {(| \vec{a} | + | \vec{b} |)}^{2}$
$\Leftrightarrow {(\vec{a} + \vec{b})}^{2} = {| \vec{a} |}^{2} + 2 | \vec{a} | . | \vec{b} | + {| \vec{b} |}^{2}$
$\Leftrightarrow {\vec{a}}^{2} + 2 \vec{a} . \vec{b} + {\vec{b}}^{2} = {\vec{a}}^{2} + 2 | \vec{a} | . | \vec{b} | + {\vec{b}}^{2}$
$\Leftrightarrow \vec{a} . \vec{b} = | \vec{a} | . | \vec{b} |$

Mà $\vec{a} . \vec{b} = | \vec{a} | . | \vec{b} | . c o s (\vec{a}, \vec{b})$
Do đó: $| \vec{a} | . | \vec{b} | = | \vec{a} | . | \vec{b} | . c o s (\vec{a}, \vec{b}) \Leftrightarrow c o s (\vec{a}, \vec{b}) = 1$
Suy ra: $(\vec{a}, \vec{b}) = 0 °$ hay hai vectơ $\vec{a}$ và $\vec{b}$ cùng hướng.
Vậy đẳng thức a) đúng khi hai vectơ $\vec{a}$ và $\vec{b}$ cùng hướng.
b) Bình phương hai vế của đẳng thức $| \vec{a} + \vec{b} | = | \vec{a} - \vec{b} |$ , ta được: ${| \vec{a} + \vec{b} |}^{2} = {| \vec{a} - \vec{b} |}^{2}$
$\Leftrightarrow {(\vec{a} + \vec{b})}^{2} = {(\vec{a} - \vec{b})}^{2}$
$\Leftrightarrow {\vec{a}}^{2} + 2 \vec{a} . \vec{b} + {\vec{b}}^{2} = {\vec{a}}^{2} - 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$
$\Leftrightarrow \vec{a} . \vec{b} = 0 \Leftrightarrow \vec{a} ⊥ \vec{b}$

Vậy đẳng thức b) đúng khi hai vectơ $\vec{a}$ và $\vec{b}$ vuông góc với nhau.

====== **** mời các bạn xem câu tiếp bên dưới **** =====
Cho |a→+b→|=0. So sánh độ dài, phương và hướng của hai vectơ a→ và b→.

Câu hỏi:

Cho $| \vec{a} + \vec{b} | = 0$ . So sánh độ dài, phương và hướng của hai vectơ $\vec{a}$ và $\vec{b}$ .

Trả lời:

Ta có: $| \vec{a} + \vec{b} | = 0$ $\Leftrightarrow \vec{a} + \vec{b} = \vec{0} \Leftrightarrow \vec{a} = - \vec{b}$ .
Khi đó $\vec{a}$ và $\vec{b}$ là hai vectơ đối nhau.
Vậy $\vec{a}$ và $\vec{b}$ cùng phương, ngược hướng và có cùng độ dài.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Bài liên quan:

Leave a Comment Hủy