Cặp số nào sau đây là nghiệm của hệ bất phương trình x−2y−2−x+y

Câu hỏi:

Cặp số nào sau đây là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x-2y<0\\ x+3y>-2\\ -x+y<3\end{array}\right..$

A. (1; 0);

B. (– 1; 0);

Đáp án chính xác

C. (– 2; 3);

D. (0; – 1).

Trả lời:

Đáp án đúng là B
Ta xét hệ phương trình: $\left\{\begin{array}{l}x-2y<0\left(1\right)\\ x+3y>-2\left(2\right)\\ -x+y<3\left(3\right)\end{array}\right..$
+) Thay x = 1 và y = 0 lần lượt vào các bất phương trình (1), (2) và (3) trong hệ, ta được:
(1) ⇔ 1 – 2.0 < 0 ⇔ 1 < 0 (vô lí);
(2) ⇔ 1 + 3.0 > – 2 ⇔ 1 > – 2 (luôn đúng);
(3) ⇔ – 1 + 0 < 3 ⇔ – 1 < 3 (luôn đúng).
Do đó cặp số (1; 0) không là nghiệm của hệ bất phương trình đã cho.
+) Thay x = – 1 và y = 0 lần lượt vào các bất phương trình (1), (2) và (3) trong hệ, ta được:
(1) ⇔ – 1 – 2.0 < 0 ⇔ – 1 < 0 (luôn đúng);
(2) ⇔ – 1 + 3.0 > – 2 ⇔ – 1 > – 2 (luôn đúng);
(3) ⇔ 1 + 0 < 3 ⇔ 1 < 3 (luôn đúng).
Do đó cặp số (– 1; 0) là nghiệm của hệ bất phương trình đã cho.
+) Thay x = – 2 và y = 3 lần lượt vào các bất phương trình (1), (2) và (3) trong hệ, ta được:
(1) ⇔ – 2 – 2.3 < 0 ⇔ – 8 < 0 (luôn đúng);
(2) ⇔ – 2 + 3.3 > – 2 ⇔ 7 > – 2 (luôn đúng);
(3) ⇔ 2 + 3 < 3 ⇔ 5 < 3 (vô lí).
Do đó cặp số (– 2; 3) không là nghiệm của hệ bất phương trình đã cho.
+) Thay x = 0 và y = – 1 lần lượt vào các bất phương trình (1), (2) và (3) trong hệ, ta được:
(1) ⇔ 0 – 2.(– 1) < 0 ⇔ 2 < 0 (vô lí);
(2) ⇔ 0 + 3.(– 1) > – 2 ⇔ – 3 > – 2 (vô lí);
(3) ⇔ 0 + (– 1) < 3 ⇔ – 1 < 3 (luôn đúng).
Do đó cặp số (0; – 1) không là nghiệm của hệ bất phương trình đã cho.
Vậy (– 1; 0) là nghiệm của hệ phương trình đã cho.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cặp số nào sau đây không là nghiệm của hệ bất phương trình x+y≤22x−3y>−2.
   
   

   Câu hỏi:
   

   Cặp số nào sau đây không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x+y\le 2\\ 2x-3y>-2\end{array}\right..$

   A. (0; 0);

   B. (1; 1);

   C. (– 1; 1);

   Đáp án chính xác

   D. (– 1; – 1).

   Trả lời:

   Đáp án đúng là C
   Xét hệ phương trình: $\left\{\begin{array}{l}x+y\le 2\left(1\right)\\ 2x-3y>-2\left(2\right)\end{array}\right..$
   +) Thay x = 0 và y = 0 lần lượt vào các bất phương trình (1) và (2) trong hệ, ta được:
   (1) ⇔ 0 + 0 ≤ 2 ⇔ 0 ≤ 2 (luôn đúng);
   (2) ⇔ 2.0 – 3.0 > – 2 ⇔ 0 > – 2 (luôn đúng).
   Do đó cặp số (0; 0) là nghiệm của hệ bất phương trình đã cho.
   +) Thay x = 1 và y = 1 lần lượt vào các bất phương trình (1) và (2) trong hệ, ta được:
   (1) ⇔ 1 + 1 ≤ 2 ⇔ 2 ≤ 2 (luôn đúng);
   (2) ⇔ 2.1 – 3.1 > – 2 ⇔ – 1 > – 2 (luôn đúng).
   Do đó cặp số (1; 1) là nghiệm của hệ bất phương trình đã cho.
   +) Thay x = – 1 và y = 1 lần lượt vào các bất phương trình (1) và (2) trong hệ, ta được:
   (1) ⇔ – 1 + 1 ≤ 2 ⇔ 0 ≤ 2 (luôn đúng);
   (2) ⇔ 2.(– 1) – 3.1 > – 2 ⇔ – 5 > – 2 (vô lí).
   Do đó cặp số (– 1; 1) không là nghiệm của hệ bất phương trình đã cho.
   +) Thay x = – 1 và y = – 1 lần lượt vào các bất phương trình (1) và (2) trong hệ, ta được:
   (1) ⇔ – 1 + (– 1) ≤ 2 ⇔ – 2 ≤ 2 (luôn đúng);
   (2) ⇔ 2.(– 1) – 3.(– 1) > – 2 ⇔ 1 > – 2 (luôn đúng).
   Do đó cặp số (– 1; – 1) là nghiệm của hệ bất phương trình đã cho.
   Vậy cặp số (– 1; 1) không là nghiệm của hệ bất phương trình đã cho.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Miền nghiệm của hệ bất phương trình 2x−5y>12x+y>−5x+y
   
   

   Câu hỏi:
   

   Miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}2x-5y>1\\ 2x+y>-5\\ x+y<-1\end{array}\right.$ là phần mặt phẳng chứa điểm có tọa độ:

   A. (0; 0);

   B. (1; 0);

   C. (0; 2);

   D. (0; – 2).

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là D
   Ta xét hệ bất phương trình $\left\{\begin{array}{l}2x-5y>1\left(1\right)\\ 2x+y>-5\left(2\right)\\ x+y<-1\left(3\right)\end{array}\right.$.
   +) Thay x = 0 và y = 0 lần lượt vào các bất phương trình (1), (2) và (3) trong hệ, ta được:
   (1) ⇔ 2.0 – 5.0 > 1 ⇔ 0 > 1 (vô lí);
   (2) ⇔ 2.0 + 0 > – 5 ⇔ 0 > – 5 (luôn đúng);
   (3) ⇔ 0 + 0 < – 1 ⇔ 0 < – 1 (vô lí).
   Do đó cặp số (0; 0) không thuộc miền nghiệm của hệ bất phương trình đã cho.
   +) Thay x = 1 và y = 0 lần lượt vào các bất phương trình (1), (2) và (3) trong hệ, ta được:
   (1) ⇔ 2.1 – 5.0 > 1 ⇔ 2 > 1 (luôn đúng);
   (2) ⇔ 2.1 + 0 > – 5 ⇔ 2 > – 5 (luôn đúng);
   (3) ⇔ 1 + 0 < – 1 ⇔ 1 < – 1 (vô lí).
   Do đó cặp số (1; 0) không thuộc miền nghiệm của hệ bất phương trình đã cho.
   +) Thay x = 0 và y = 2 lần lượt vào các bất phương trình (1), (2) và (3) trong hệ, ta được:
   (1) ⇔ 2.0 – 5.2 > 1 ⇔ – 10 > 1 (vô lí);
   (2) ⇔ 2.0 + 2 > – 5 ⇔ 2 > – 5 (luôn đúng);
   (3) ⇔ 0 + 2 < – 1 ⇔ 2 < – 1 (vô lí).
   Do đó cặp số (0; 2) không thuộc miền nghiệm của hệ bất phương trình đã cho.
   +) Thay x = 0 và y = – 2 lần lượt vào các bất phương trình (1), (2) và (3) trong hệ, ta được:
   (1) ⇔ 2.0 – 5.(– 2) > 1 ⇔ 10 > 1 (luôn đúng);
   (2) ⇔ 2.0 + (– 2) > – 5 ⇔ – 2 > – 5 (luôn đúng);
   (3) ⇔ 0 + (– 2) < – 1 ⇔ – 2 < – 1 (luôn đúng).
   Do đó cặp số (0; – 2 ) thuộc miền nghiệm của hệ bất phương trình đã cho.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
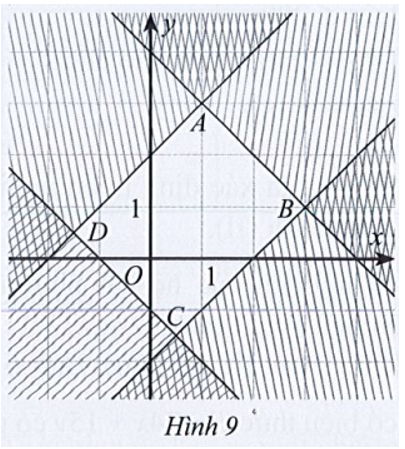
3. Miền đa giác ABCD ở Hình 9 là miền nghiệm của hệ bất phương trình:
   
   

   Câu hỏi:
   

   Miền đa giác ABCD ở Hình 9 là miền nghiệm của hệ bất phương trình:
   

   A. $\left\{\begin{array}{l}x+y\le 4\\ x+y\ge -1\\ x-y\le 2\\ x-y\ge -2\end{array}\right.$

   Đáp án chính xác

   B. $\left\{\begin{array}{l}x-y\le 4\\ x-y\ge -1\\ x+y\le 2\\ x+y\ge -2\end{array}\right.$

   C. $\left\{\begin{array}{l}x+y\le 1\\ x+y\ge -4\\ x-y\le 2\\ x-y\ge -2\end{array}\right.$

   D. $\left\{\begin{array}{l}x-y\le 1\\ x-y\ge -4\\ x+y\le 2\\ x+y\ge -2\end{array}\right.$

   Trả lời:

   Đáp án đúng là A
   +) Gọi d₁ là đường thẳng đi qua hai điểm A và D. Đường thẳng cắt hai trục tọa độ tại hai điểm (– 2; 0) và (0; 2) nên phương trình đường thẳng d là: $\frac{x}{-2}+\frac{y}{2}=1\iff x-y=-2$.
   Lấy điểm O(0; 0) ta có 0 – 0 = 0 > – 2.
   Mà điểm O thuộc miền nghiệm của hệ bất phương trình nên ta có bất phương trình x – y ≥ – 2.
   +) Gọi d₂ là đường thẳng đi qua hai điểm A và D. Đường thẳng cắt hai trục tọa độ tại hai điểm (4; 0) và (0; 4) nên phương trình đường thẳng d là: $\frac{x}{4}+\frac{y}{4}=1\iff x+y=4$.
   Lấy điểm O(0; 0) ta có 0 + 0 = 0 < 4.
   Mà điểm O thuộc miền nghiệm của hệ bất phương trình nên ta có bất phương trình x + y ≤ 4.
   +) Gọi d₃ là đường thẳng đi qua hai điểm B và C. Đường thẳng cắt hai trục tọa độ tại hai điểm (2; 0) và (0; – 2) nên phương trình đường thẳng d là: $\frac{x}{2}+\frac{y}{-2}=1\iff x-y=2$.
   Lấy điểm O(0; 0) ta có 0 – 0 = 0 < 2.
   Mà điểm O thuộc miền nghiệm của hệ bất phương trình nên ta có bất phương trình x – y ≤ 2.
   +) Gọi d₄ là đường thẳng đi qua hai điểm D và C. Đường thẳng cắt hai trục tọa độ tại hai điểm (– 1; 0) và (0; – 1) nên phương trình đường thẳng d là: $\frac{x}{-1}+\frac{y}{-1}=1\iff x+y=-1$.
   Lấy điểm O(0; 0) ta có 0 + 0 = 0 > – 1.
   Mà điểm O thuộc miền nghiệm của hệ bất phương trình nên ta có bất phương trình x + y ≥ – 1.
   Từ đó ta có hệ bất phương trình sau: $\left\{\begin{array}{l}x-y\ge -2\\ x+y\le 4\\ x-y\le 2\\ x+y\ge -1\end{array}\right.$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Giá trị nhỏ nhất của biểu thức F = – x + y trên miền nghiệm của hệ bất phương trình −2x+y≤2−x+2y≥4x+y≤5.
   
   

   Câu hỏi:
   

   Giá trị nhỏ nhất của biểu thức F = – x + y trên miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-2x+y\le 2\\ -x+2y\ge 4\\ x+y\le 5\end{array}\right.$.

   A. 0

   Đáp án chính xác

   B. 1

   C. 2

   D. 3

   Trả lời:

   Đáp án đúng là B
   Bài toán đã cho trở thành tìm nghiệm (x; y) của hệ bất phương trình $\left\{\begin{array}{l}-2x+y\le 2\\ -x+2y\ge 4\\ x+y\le 5\end{array}\right.$ sao cho biểu thức F = – x + y đạt giá trị nhỏ nhất.
   Trước hết ta xác định miền nghiệm của hệ bất phương trình đã cho:
   Ta có ba đường thẳng: d₁: – 2x + y = 2; d₂: – x + 2y = 4 và d₃: x + y = 5.
   +) Lấy O(0; 0) có – 2.0 + 0 = 0 < 2. Do đó miền nghiệm của bất phương trình – 2x + y ≤ 2 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₁.
   +) Lấy O(0; 0) có – 0 + 2.0 = 0 < 4. Do đó miền nghiệm của bất phương trình – x + 2y ≥ 4 là nửa mặt phẳng không chứa điểm O(0; 0) có bờ là đường thẳng d₂.
   +) Lấy O(0; 0) có 0 + 0 = 0 < 5. Do đó miền nghiệm của bất phương trình x + y ≤ 5 là nửa mặt phẳng chứa điểm O(0; 0) và có bờ là đường thẳng d₃.
   Miền nghiệm của hệ bất phương trình là miền tam giác ABC với A(0; 2), B(1; 4) và C(2; 3) như trong hình vẽ sau:
   
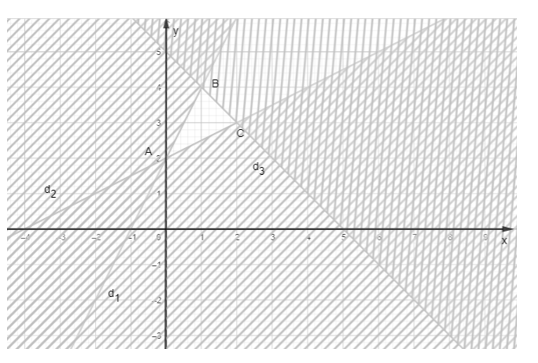
   Ta đã chứng minh được biểu thức F = – x + y có giá trị nhỏ nhất tại các đỉnh của tam giác ABC.
   Tại điểm A, với x = 0, y = 2 thì F = – 0 + 2 = 2.
   Tại điểm B, với x = 1, y = 4 thì F = – 1 + 4 = 3.
   Tại điểm C, với x = 2, y = 3 thì F = – 2 + 3 = 1.
   Vậy giá trị nhỏ nhất của biểu thức F là 1 khi x = 2 và y = 3.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Biểu diễn miền nghiệm của hệ bất phương trình sau: a) x−2y≤3x+y≥−3;
   
   

   Câu hỏi:
   

   Biểu diễn miền nghiệm của hệ bất phương trình sau:
   a) $\left\{\begin{array}{l}x-2y\le 3\\ x+y\ge -3;\end{array}\right.$

   Trả lời:

   a) Ta có hai đường thẳng: d₁: x – 2y = 3; d₂: x + y = – 3.
   +) Lấy O(0; 0) không thuộc vào đường thẳng d₁ có 0 – 2.0 = 0 < 3. Do đó miền nghiệm của bất phương trình x – 2y ≤ 3 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₁.
   +) Lấy O(0; 0) không thuộc đường thẳng d₂ có 0 + 0 = 0 > – 3. Do đó miền nghiệm của bất phương trình x + y ≥ – 3 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₂.
   Miền nghiệm của hệ bất phương trình là miền không tô màu như trong hình vẽ sau:
   

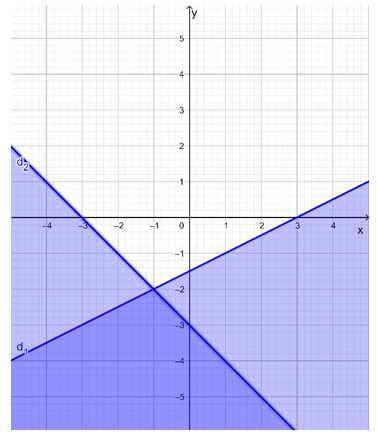
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====