Biểu thức nào sau đây có bảng xét dấu như:

Câu hỏi:

Biểu thức nào sau đây có bảng xét dấu như:

A. $f\left(x\right)=3x-15.$

Đáp án chính xác

B. $f\left(x\right)=3x+15$.

C. $f\left(x\right)=-45x^2-9.$

D. $f\left(x\right)=6\left(x-10\right)-3x+55.$

Trả lời:

Chọn đáp án A
Dựa vào bảng xét dấu, ta có: f(x) là nhị thức bậc nhất và f(x) = 0 khi x = 5, hơn nữa hệ số a > 0.
Do đó chỉ có đáp án A thỏa mãn.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tìm góc giữa 2 đường thẳng Δ1: 2x – y – 10 = 0 và Δ2: x – 3y – 9 = 0:
   
   

   Câu hỏi:
   

   Tìm góc giữa 2 đường thẳng Δ₁: 2x – y – 10 = 0 và Δ₂: x – 3y – 9 = 0:

   A. 60^o

   B. 45^o

   Đáp án chính xác

   C. 90^o

   D. 0^o

   Trả lời:

   Chọn đáp án B.
   Ta có: Δ₁: 2x – y – 10 = 0 có VTPT $\overrightarrow{n_1}\left(2;-1\right)$
   Δ₂: x – 3y – 9 = 0 có VTPT $\overrightarrow{n_2}\left(1;-3\right)$
   Khi đó, ta có: cos(Δ₁,Δ₂) =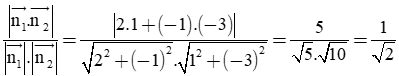
    
   Suy ra góc giữa hai đường thẳng Δ₁ và Δ₂ là: 45⁰.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tập nghiệm của bất phương trình 4−2x2x+6≥0
   
   

   Câu hỏi:
   

   Tập nghiệm của bất phương trình $\left(4-2x\right)\left(2x+6\right)\ge 0$

   A. $\left(-3;2\right).$

   B. $\left(-\infty ;-3\right)\cup \left(2;+\infty \right).$

   C. $\left[-3;2\right].$

   Đáp án chính xác

   D. $\left(-\infty ;-3\right]\cup \left[2;+\infty \right).$

   Trả lời:

   Chọn đáp án C
   $\left(4-2x\right)\left(2x+6\right)\ge 0$$\iff -4x^2-4x+24\ge 0$
   Ta có: – 4x² – 4x + 24 = 0 $\iff \left[\begin{array}{l}x=2\\ x=-3\end{array}\right.$
   Áp dụng định lý dấu của tam thức bậc hai ta có: $-3\le x\le 2.$
   Vậy tập nghiệm của bất phương trình là: $S=\left[-3;2\right].$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Véctơ nào sau đây là một véctơ pháp tuyến của đường thẳng – x + 3y + 2 = 0?
   
   

   Câu hỏi:
   

   Véctơ nào sau đây là một véctơ pháp tuyến của đường thẳng – x + 3y + 2 = 0?

   A. $\overrightarrow{n_1}=\left(-1;3\right)$.

   Đáp án chính xác

   B. $\overrightarrow{n_2}=\left(3;1\right)$.

   C. $\overrightarrow{n_3}=\left(-3;1\right)$.

   D. $\overrightarrow{n_4}=\left(1;3\right)$.

   Trả lời:

   Chọn đáp án A
   Véctơ pháp tuyến của đường thẳng – x + 3y + 2 = 0 là $\overrightarrow{n}\left(-1;3\right)$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tính khoảng cách d từ điểm A(1;2) đến đường thẳng Δ: 12x + 5y + 4 = 0.
   
   

   Câu hỏi:
   

   Tính khoảng cách d từ điểm A(1;2) đến đường thẳng Δ: 12x + 5y + 4 = 0.

   A. $d=\frac{11}{12}$.

   B. d = 2.

   Đáp án chính xác

   C. d = 4.

   D. $d=\frac{13}{17}$.

   Trả lời:

   Chọn đáp án B
   Khoảng cách từ điểm A đến đường thẳng Δ là:
   $d\left(A;\Delta \right)=\frac{\left|12.1+5.2+4\right|}{\sqrt{{12}^2+5^2}}=2$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Hệ bất phương trình 3−x≥0x+1≥0có tập nghiệm là :
   
   

   Câu hỏi:
   

   Hệ bất phương trình $\left\{\begin{array}{l}3-x\ge 0\\ x+1\ge 0\end{array}\right.$có tập nghiệm là :

   A. $\left(-1;3\right].$

   B. $\left[-1;3\right].$

   Đáp án chính xác

   C. $ℝ.$

   D. $\varnothing .$

   Trả lời:

   Chọn đáp án B
   Ta có: $\left\{\begin{array}{l}3-x\ge 0\\ x+1\ge 0\end{array}\right.\iff \left\{\begin{array}{l}x\le 3\\ x\ge -1\end{array}\right.\iff -1\le x\le 3$
   Vậy tập nghiệm của hệ phương trình: $S=\left[-1;3\right].$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====