Giải SBT Toán lớp 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông
Giải trang 64 Tập 1
Bài 4.31 trang 64 Tập 1: Trong mỗi hình sau (H.4.33) có các cặp tam giác vuông nào bằng nhau?
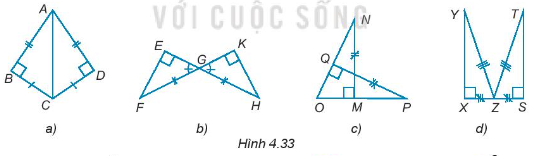
Hướng dẫn giải
+) Hình a:
Xét ∆ABC và ∆ADC ta có:
AB = AD (giả thiết)
= = 90° (giả thiết)
BC = CD (giả thiết)
Do đó, ∆ABC = ∆ADC (hai cạnh góc vuông).
+) Hình b
Xét ∆EFG và ∆KHG ta có:
GF = GH (giả thiết)
= = 90° (giả thiết)
= (hai góc đối đỉnh)
Do đó, ∆EFG = KHG (góc nhọn – cạnh huyền)
+) Hình c:
Tam giác OMN vuông tại M nên .
Tam giác OQP vuông tại Q nên .
Do đó, .
Xét ∆OMN và ∆OQP ta có:
MN = PQ (giả thiết)
= = 90o (giả thiết)
(chứng minh trên)
Do đó, ∆OMN = ∆OQP (góc nhọn – cạnh góc vuông).
+) Hình d:
Xét ∆XYZ và ∆STZ ta có:
YZ = TZ (giả thiết)
= = 90° (giả thiết)
XZ = SZ (giả thiết)
Do đó, ∆XYZ = ∆STZ (cạnh huyền – cạnh góc vuông).
Bài 4.32 trang 64 Tập 1: Cho các điểm A, B, C, D, E như Hình 4.34. Biết rằng E là trung điểm của BC, chứng minh rằng ∆ABE = ∆DCE.
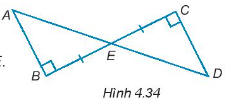
Hướng dẫn giải
Xét ∆ABE và ∆DCE ta có:
∆ABE = ∆CDE (góc nhọn – cạnh góc vuông).
Giải trang 65 Tập 1
Bài 4.33 trang 65 Tập 1: Cho các điểm A, B, C, D, E như Hình 4.35. Biết rằng AC vuông góc với BD, EA = EB và EC = ED.
Chứng minh rằng:
a) ∆AED = ∆BEC.
b) ∆ABC = ∆BAD.
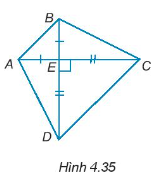
Hướng dẫn giải
a) Xét ∆AED và ∆BEC ta có:
AE = BE (giả thiết)
= = 90° (do AC và DB vuông góc với nhau)
ED = EC (giả thiết)
Do đó, ∆AED = ∆BEC (hai cạnh góc vuông).
b) Ta có: AC = AE + EC; BD = BE + ED. Mà AE = BE; EC = ED nên AC = BD.
Vì ∆AED = ∆BEC nên AD = BC (hai cạnh tương ứng)
Xét ∆ABC và ∆BAD có:
BC = AD (chứng minh trên)
AB chung
AC = BD (chứng minh trên)
Do đó, ∆ABC = ∆BAD (c – c – c).
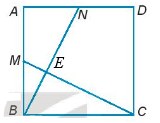
Bài 4.34 trang 65 Tập 1: Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh rằng BN = CM và BN ⊥ CM.
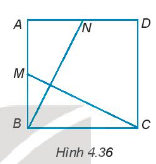
Hướng dẫn giải
Vì ABCD là hình vuông nên AB = BC = CD = DA.
Vì N là trung điểm của AD nên AN = ND = .
Vì M là trung điểm của AB nên AM = MB = .
Mà AB = AD nên AN = BM.
Xét ∆ANB và ∆BMC có:
AN = BM (chứng minh trên)
AB = BC (chứng minh trên)
= = 90° (do ABCD là hình vuông)
Do đó, ∆ANB = ∆BMC (hai cạnh góc vuông)
Suy ra, BN = CM (hai cạnh tương ứng).
Gọi E là giao điểm của BN và CM.
Do ∆ANB = ∆BMC nên .
Từ định lí tổng ba góc trong tam giác BME và tam giác ABN, ta suy ra:
.
Vậy BN vuông góc với CM tại E.
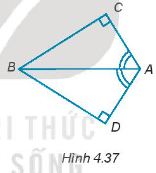
Bài 4.35 trang 65 Tập 1: Cho bốn điểm A, B, C, D như Hình 4.37. Biết rằng , hãy chứng minh CB = DB.
Hướng dẫn giải
Xét ∆ABC và ∆ABD có:
AB chung
= (giả thiết)
= = 90° (giả thiết)
Do đó, ∆ABC = ∆ABD (cạnh huyền – góc nhọn).
Suy ra CB = DB.
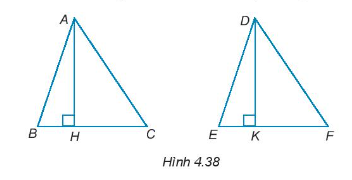
Bài 4.36 trang 65 Tập 1: Cho AH và DK lần lượt là hai đường cao của hai tam giác ABC và DEF như Hình 4.38. Biết rằng ∆ABC = ∆DEF, hãy chứng minh AH = DK.
Hướng dẫn giải
Vì ∆ABC = ∆DEF nên
(các góc tương ứng và các cạnh tương ứng bằng nhau).
Vì AH là đường cao của tam giác ABC nên AH vuông góc với BC. Do đó, .
Vì DK là đường cao của tam giác DEF nên DK vuông góc với EF. Do đó, .
Xét ∆ABH và ∆DEK có:
(chứng minh trên)
AB = DE (chứng minh trên)
(chứng minh trên)
Do đó, ∆ABH = ∆DEK (cạnh huyền – góc nhọn).
Suy ra AH = DK.
Giải trang 66 Tập 1
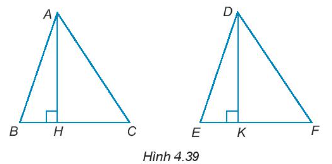
Bài 4.37 trang 66 Tập 1: Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh rằng:
a) Nếu AB = DE; BC = EF và AH = DK thì ∆ABC = ∆DEF;
b) Nếu AB = DE, AC = DF và AH = DK thì ∆ABC = ∆DEF.
Hướng dẫn giải
a)
Vì AH là đường cao của tam giác ABC nên AH vuông góc với BC. Do đó, .
Vì DK là đường cao của tam giác DEF nên DK vuông góc với EF. Do đó, .
Xét ∆ABH và ∆DEK có:
(chứng minh trên)
AB = DE (giả thiết)
AH = DK (giả thiết)
Do đó, ∆ABH = ∆DEK (cạnh huyền – cạnh góc vuông).
Suy ra, (hai góc tương ứng).
Xét ∆ABC và ∆DEF có:
(chứng minh trên)
AB = DE (giả thiết)
BC = EF (giả thiết)
Do đó, ∆ABC = ∆DEF (c – g – c).
b) Vì AH là đường cao của tam giác ABC nên AH vuông góc với BC. Do đó, .
Vì DK là đường cao của tam giác DEF nên DK vuông góc với EF. Do đó, .
Xét ∆ABH và ∆DEK có:
(chứng minh trên)
AB = DE (giả thiết)
AH = DK (giả thiết)
Do đó, ∆ABH = ∆DEK (cạnh huyền – cạnh góc vuông).
Suy ra, BH = EK.
Xét ∆ACH và ∆DFK có:
(chứng minh trên)
AC = DF (giả thiết)
AH = DK (giả thiết)
Do đó, ∆ACH = ∆DFK (cạnh huyền – cạnh góc vuông).
Suy ra, CH = FK.
Ta có: BC = BH + HC; EF = EK + FK. Mà BH = EK; HC = FK nên BC = EF.
Xét ∆ABC và ∆DEF có:
BC = EF (chứng minh trên)
AC = DF (giả thiết)
AB = DE (giả thiết)
Do đó, ∆ABC = ∆DEF (c – c – c).
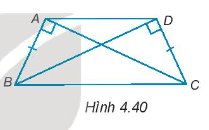
Bài 4.38 trang 66 Tập 1: Cho bốn điểm A, B, C, D như Hình 4.40, trong đó AB = DC. Chứng minh rằng:
a) AC = BD.
b) AD // BC.
Hướng dẫn giải
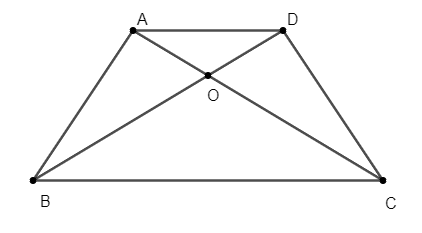
Gọi giao điểm của AC và BD là O.
a) Xét ∆ABC và ∆DCB có:
(giả thiết)
AB = CD (giả thiết)
BC chung
Do đó, ∆ABC = ∆DCB (cạnh huyền – cạnh góc vuông).
Suy ra, AC = BD (hai cạnh tương ứng).
b) Vì ∆ABC = ∆DCB nên (hai góc tương ứng)
Xét tam giác OBC có:
= 180°.
Mà do nên = 180°
Suy ra = 180° –
Do đó, (1)
Xét ∆ABD và ∆DCA có:
AB = CD (giả thiết)
BD = AC (chứng minh trên)
AD chung
Do đó, ∆ABD = ∆DCA (c – c – c).
Suy ra, .
Xét tam giác OAD có:
= 180°.
Mà do nên = 180°
Do đó, (2)
Mà (hai góc đối đỉnh) (3)
Từ (1), (2), (3) suy ra, hay .
Mà hai góc này ở vị trí so le trong nên AD // BC.
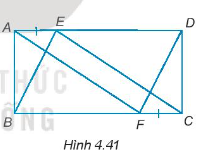
Bài 4.39 trang 66 Tập 1: Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF (H.4.41). Chứng minh rằng:
a) AF = CE.
b) AF // CE.
Hướng dẫn giải
a) Vì ABCD là hình chữ nhật nên AD = BC; AB = CD.
Ta có: AD = AE + ED; BC = BF + FC mà FC = AE (gt) và AD = BC nên ED = BF.
Vì ABCD là hình chữ nhật nên .
Xét ∆ABF và ∆CDE có:
AB = CD (chứng minh trên)
BF = ED (chứng minh trên)
(do )
Do đó, ∆ABF = ∆CDE (hai cạnh góc vuông).
Suy ra, AF = CE.
b) Vì ∆ABF = ∆CDE nên (hai góc tương ứng).
Lại có ABCD là hình chữ nhật nên AD // BC nên (hai góc so le trong).
Ta có: ; nên .
Mà hai góc này ở vị trí đồng vị
Nên AF // CE (điều phải chứng minh).
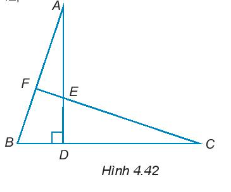
Bài 4.40 trang 66 Tập 1: Cho năm điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE.
a) Chứng minh rằng AB = CE.
b) Cho đường thẳng CE cắt AB tại F. Chứng minh rằng .
Hướng dẫn giải
a) Xét ∆ABD và ∆CED có:
(giả thiết)
DA = DC (giả thiết)
DB = DE (giả thiết)
Do đó, ∆ABD = ∆CED (hai cạnh góc vuông).
Suy ra, AB = CE (hai cạnh tương ứng).
b) Vì ∆ABD = ∆CED nên (hai góc tương ứng).
Lại có: (do tam giác ABD vuông ở D) nên .
Xét tam giác BFC có:
Mà chính là góc và chính là góc .
Do đó, + = 90°.
Nên + 90° = 180°
Suy ra = 180° – 90° = 90° (điều phải chứng minh).
Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Bài 15: Các trường hợp bằng nhau của tam giác vuông
Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Ôn tập chương 4
Bài 17: Thu thập và phân loại dữ liệu