Bài tập hay nhất về Hai góc đối đỉnh hình học lớp 7 có lời giải

Tài liệu Hai góc đối đỉnh hình học lớp 7 gồm các nội dung chính sau:

A. Phương pháp giải

– tóm tắt lý thuyết ngắn gọn.

B. Một số ví dụ

– gồm 4 ví dụ minh họa đa dạng của các dạng bài tập Hai góc đối đỉnh hình học lớp 7 có lời giải chi tiết.

C. Bài tập vận dụng

– gồm 12 bài tập vận dụng có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng bài tập Hai góc đối đỉnh hình học lớp 7.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

HAI GÓC ĐỐI ĐỈNH HÌNH HỌC LỚP 7

A. Phương pháp giải

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia (h.1.1).

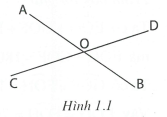
2. Hai góc đối đỉnh thì bằng nhau: $\widehat{AOC}=\widehat{BO\text{D}};\widehat{AO\text{D}}=\widehat{BOC}$.

B. Một số ví dụ

Ví dụ 1: Cho góc bẹt AOB. Trên hai nửa mặt phẳng đối nhau bờ AB vẽ hai tia OM và ON sao cho $\widehat{AOM}=\widehat{BON}$. Chứng minh rằng hai góc AON và BOM là hai góc đối đỉnh.        

Giải (h.1.2)

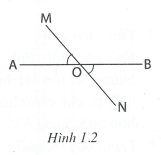
* Tìm cách giải

Để chứng tỏ hai góc AON và BOM là hai góc đối đỉnh, ta cần chứng tỏ mỗi cạnh của góc này là tia đối một cạnh của góc kia. Vì đã có hai tia OA, OB đối nhau nên chỉ còn phải chứng tỏ hai tia OM, ON đối nhau bằng cách chứng tỏ MON là góc bẹt.

* Trình bày lời giải

Góc AOB là góc bẹt nên hai tia OA, OB đối nhau. Hai góc AOM và BOM kề bù nên $\widehat{AOM}+\widehat{BOM}=180°$.

Mặt khác $\widehat{AOM}=\widehat{BON}$ (đề bài cho) nên $\widehat{BON}+\widehat{BOM}=180°$.

Suy ra $\widehat{MON}=180°$. Vậy hai tia OM, ON đối nhau.

Hai góc AON và BOM có mỗi cạnh của góc này là tia đối một cạnh của góc kia nên chúng là hai góc đối đỉnh.

Ví dụ 2: Cho hai đường thẳng EF và GH cắt nhau tại O tạo thành bốn góc không kể góc bẹt. Biết tổng $\widehat{EOG}+\widehat{GOF}+\widehat{FOH}=250°$. Tính số đo của bốn góc tạo thành.

Giải (h.1.3)

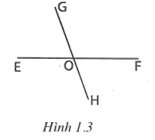
* Tìm cách giải

Để tính được số đo của bốn góc tạo thành, trước tiên cần tính được số đo của một trong bốn góc đó.

* Trình bày lời giải

Ta có $\widehat{EOG}+\widehat{GOF}+\widehat{FOH}=250°$ (đề bài cho), mà $\widehat{EOG}+\widehat{GOF}=180°$ (hai góc kề bù) nên $\widehat{F\text{O}H}=250°-180°=70°$.

Ta có $\widehat{GOF}+\widehat{FOH}=180°$ (hai góc kề bù) $\Rightarrow \widehat{GOF}=180°-70°=110°$.

Vậy $\widehat{EOG}=\widehat{F\text{O}H}=70°$ (hai góc đối đỉnh); $\widehat{HOE}=\widehat{GOF}=110°$ (hai góc đối đỉnh).

* Nhận xét: Sau khi tính được số đo của một góc, ta tính được số đo của ba góc còn lại nhờ vận dụng tính chất của hai góc kề bù, hai góc đối đỉnh.

Ví dụ 3: Cho bốn đường thẳng cắt nhau tại một điểm. Xét các góc không có điểm trong chung, chứng tỏ rằng tồn tại hai góc nhỏ hơn hoặc bằng .

Giải (h.1.4)

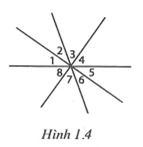
* Tìm cách giải

Hai góc đối đỉnh thì bằng nhau. Do đó để chứng tỏ tồn tại hai góc nhỏ hơn hoặc bằng $45°$, ta chỉ cần chứng tỏ tồn tại một góc nhỏ hơn hoặc bằng .

* Trình bày lời giải

Bốn đường thẳng cắt nhau tại một điểm tạo ra 8 góc không có điểm trong chung.

Nếu tất cả các góc này đều lớn hơn $45°$ thì tổng của chúng lớn hơn $45°.8=360°$. Điều này vô lí, vì tổng của 8 góc này đúng bằng $360°$

Vậy phải tồn tại một góc nhỏ hơn hoặc bằng $45°$. Góc này và góc đối đỉnh với nó bằng nhau. Do đó tồn tại hai góc nhỏ hơn hoặc bằng $45°$.

Ví dụ 4: Trong hình 1.5, hai góc AOC và BOD là hai góc đối đỉnh. Hai tia OE, OF là hai tia đối nhau. Cho biết tia OE là tia phân giác của góc AOC, chứng tỏ rằng tia OF là tia phân giác của góc BOD.

Giải (h.1.5)

* Tìm cách giải

Ta cần chứng tỏ $\widehat{O_3}=\widehat{O_4}$. Muốn vậy phải sử dụng tính chất của hai góc đối đỉnh.

* Trình bày lời giải

Hai góc AOC và BOD là hai góc đối đỉnh nên các tia OA, OB đối nhau, các tia OC, OD đối nhau. Ngoài ra, hai tia OE, OF cũng đối nhau nên ta có $\widehat{O_1}=\widehat{O_3};\widehat{O_2}=\widehat{O_4}$ (hai góc đối đỉnh). Vì $\widehat{O_1}=\widehat{O_2}$ (đề bài cho) nên $\widehat{O_3}=\widehat{O_4}$.         (1)

Mặt khác, tia OF nằm giữa hai tia OB, OD.  (2) 

nên từ (1) và (2) suy ra tia OF là tia phân giác của góc BOD.

Xem thêm