20 câu Trắc nghiệm Đại lượng tỉ lệ thuận (Kết nối tri thức) có đáp án 2023 – Toán lớp 7

Trắc nghiệm Toán 7 Bài 22: Đại lượng tỉ lệ thuận

I. Nhận biết

Câu 1. Cho biết đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ –$\frac{1}{2}$. Hãy biểu diễn y theo x.

A. y = –2x;

B. y = –$\frac{1}{2}$x;

C. y = 2x;

D. y = $\frac{1}{2}$x.

Hướng dẫn giải

Đáp án: A

Giải thích:

Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ a thì đại lượng x cũng tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ $\frac{\text{1}}{\text{a}}$.

Như vậy y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ –2 thì đại lượng x cũng tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ –$\frac{1}{2}$.

Khi y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ –2 thì ta biểu diễn y theo x qua công thức y = –2x.

Vậy đáp án A đúng.

Câu 2. Chọn câu sai. Nếu y = 2x thì ta nói

A. y tỉ lệ thuận với x theo hệ số tỉ lệ 2;

B. x tỉ lệ thuận với y theo hệ số tỉ lệ $\frac{1}{2}$;

C. Cả A và B đều đúng;

D. Cả A và B đều sai.

Hướng dẫn giải

Đáp án: D

Giải thích:

Nếu đại lượng y liên hệ với đại lượng x theo công thức y = 2x thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ 2. Khẳng định A đúng.

Khi y tỉ lệ thuận với x theo hệ số tỉ lệ 2 thì x tỉ lệ thuận với y theo hệ số tỉ lệ $\frac{1}{2}$. Khẳng định B đúng.

Như vậy khẳng định C đúng. Khẳng định D sai.

Chọn đáp án D.

Câu 3. Cho biết đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ a ( a khác 0) . Hãy biểu diễn y theo x.

A. x = ay;

B. y = –ax;

C. y = ax;

D. y = x.

Hướng dẫn giải

Đáp án: C

Giải thích:

Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ a nên y liên hệ với x theo công thức y = ax với a khác 0.

Vậy đáp án đúng là C.

Câu 4. Chọn câu đúng. Nếu y = ax ( a khác 0 ) thì ta nói

A. y tỉ lệ thuận với x theo hệ số tỉ lệ a;

B. x tỉ lệ thuận với y theo hệ số tỉ lệ a;

C. a tỉ lệ thuận với x theo hệ số tỉ lệ y;

D. a tỉ lệ thuận với y theo hệ số tỉ lệ x.

Hướng dẫn giải

Đáp án: A

Giải thích:

Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ a nên y liên hệ với x theo công thức y = ax với a khác 0.

Vậy đáp án đúng là C.

Câu 5. Chọn câu đúng. Nếu y = 3x thì ta nói

A. y tỉ lệ thuận với x theo hệ số tỉ lệ 3;

B. y tỉ lệ thuận với x theo hệ số tỉ lệ 3;

C. y không tỉ lệ thuận với x;

D. Không kết luận được điều gì về x và y.

Hướng dẫn giải

Đáp án: A

Giải thích:

Nếu đại lượng y liên hệ với đại lượng x theo công thức y = ax với a khác 0 thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ a ( nhận biết đại lượng tỉ lệ thuận).

Như vậy nếu đại lượng y liên hệ với đại lượng x theo công thức y = 3x thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ 3.

Vậy chọn đáp án A.

II. Thông hiểu

Câu 1. Cho x và y là hai đại lượng tỉ lệ thuận, khi x = 5 thì y = 15. Hệ số tỉ lệ k của y đối với x là:

A. 3;

B. 10;

C. 75;

D. $\frac{1}{3}$.

Hướng dẫn giải

Đáp án: A

Giải thích:

Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k nên y liên hệ với x theo công thức y = kx với k khác 0.

Khi x = 5 thì y = 15 nên ta có 15 = 5k. Suy ra k = 3.

Vậy chọn đáp án A.

Câu 2. Cho y tỉ lệ thuận với x theo hệ số tỉ lệ 3. Biết x + y = 40. Tìm x, y.

A. x = 10, y = 30;

B. x = 30, y = 10;

C. x = 20, y = 20 ;

D. x = 15, y = 25.

Hướng dẫn giải

Đáp án: A

Giải thích:

Do y tỉ lệ thuận với x theo hệ số tỉ lệ 3 nên y liên hệ với x theo công thức y = 3x.

Theo đề bài x + y = 40

⇒ x + 3x = 40

⇒ 4x = 40

⇒ x = 10

⇒ y = 3x = 30.

Vậy x = 10 và y = 30.

Chọn đáp án A.

Câu 3. Cho biết x và y là hai đại lượng tỉ lệ thuận. Khi x = 3 thì y = 6. Khi y = 10 thì giá trị tương ứng của x là

A. 20;

B. 3;

C. 5;

D. Không đáp án nào đúng.

Hướng dẫn giải

Đáp án: C

Giải thích:

Do x và y là hai đại lượng tỉ lệ thuận nên ta có thể biểu diễn y theo x qua công thức:

y = ax với a khác 0.

Khi x = 3 thì y = 6. Như vậy a = y : x = 6 : 3 = 2.

Ta được công thức biểu diễn y theo x là: y = 2x.

Khi y = 10 thì 2x = 10. Suy ra x = 5.

Vậy khi y = 10 thì giá trị tương ứng của x là 5.

Chọn đáp án C.

Câu 4. Cho biết đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ $\frac{-1}{3}$. Cặp giá trị nào thỏa mãn trong các cặp giá trị tương ứng với hai đại lượng đã cho sau đây:

A. x = 1, y = –3;

B. x = 2, y = 3;

C. x = –3, y = 1 ;

D. x = 3, y = 1.

Hướng dẫn giải

Đáp án: A

Giải thích:

Đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ $\frac{-1}{3}$ nên ta biểu diễn x theo y qua công thức x = $\frac{-1}{3}$y .

Ta có 1 = $\frac{-1}{3}$.(–3) đúng với công thức x = $\frac{-1}{3}$y  nên cặp x = 1, y = –3 thỏa mãn. Đáp án A đúng.

Ta có 2 ≠ $\frac{-1}{3}$ . 3 không thỏa mãn công thức x = $\frac{-1}{3}$y  nên cặp x = 2, y = 3 không thỏa mãn. Đáp án B sai.

Ta có –3 ≠ $\frac{-1}{3}$ . 1 không thỏa mãn công thức x = $\frac{-1}{3}$y  nên cặp x = –3, y = 1 không thỏa mãn. Đáp án C sai.

Ta có 3 ≠ $\frac{-1}{3}$ . 1 không thỏa mãn công thức x = $\frac{-1}{3}$y  nên cặp x = 3, y = 1 không thỏa mãn. Đáp án D sai.

Vậy chọn đáp án A.

Câu 5. Giả sử x và y là hai đại lượng tỉ lệ thuận trong đó x₁, x₂ là hai giá trị khác nhau của x và y₁, y₂ là hai giá trị của y. Tính x₁ biết x₂ = 3, y₁ = 7, y₂ = 9.

A. 21;

B. $\frac{7}{3}$;

C. $\frac{3}{7}$;

D. 14.

Hướng dẫn giải

Đáp án: B

Giải thích:

Ta có x và y là hai đại lượng tỉ lệ thuận nên có thể biểu diễn y theo x qua công thức

y = ax với a khác 0.

Thay x₂ = 3 và y₂ = 9 vào công thức y = ax ta được 9 = 3a. Suy ra a = 3.

Viết lại công thức y = 3x.

Như vậy y₁ = 3x₁ nên x₁ = y₁ : 3 = $\frac{7}{3}$.

Vậy x₁ = $\frac{7}{3}$. Chọn đáp án B.

Câu 6. Giả sử x và y là hai đại lượng tỉ lệ thuận x1 , x2 là hai giá trị khác nhau của x có tổng bằng 7 và y1 , y2 là hai giá trị của y có tổng bằng 21. Biểu diễn y theo x.

A. y = –3x;

B. y = $\frac{1}{3}$ x;  

C. y = –$\frac{1}{3}$x;

D. y = 3x.

Hướng dẫn giải

Đáp án: D

Giải thích:

Do x và y là hai đại lượng tỉ lệ thuận nên ta có thể biểu diễn y theo x qua công thức

y = ax.

Vì x và y là hai đại lượng tỉ lệ thuận nên ta có: $\frac{y_1}{x_1}=\frac{y_2}{x_2}$

Áp dụng tính chất dãy tỉ số bằng nhau ta được: $\frac{y_1}{x_1}=\frac{y_2}{x_2}=\frac{y_1+y_2}{x_1+x_2}=\frac{21}{7}=3$

Suy ra a = 3 nên ta có hàm số y = 3x.

Vậy chọn đáp án D.

Câu 7. Cho biết x và y là hai đại lượng tỉ lệ thuận theo hệ số k. Khi x = 32 thì y = 8. Công thức biểu diễn y theo x là:

A. y = –4x;

B. y = 4x;

C. y = x;

D. y = –x.

Hướng dẫn giải

Đáp án: C

Giải thích:

Do x và y là hai đại lượng tỉ lệ thuận nên ta biểu diễn y theo x qua công thức y = ax với a khác 0.

Thay x = 32 và y = 8 vào công thức y = ax ta được: 8 = 32a

Suy ra a = $\frac{1}{4}$.

Như vậy ta được công thức biểu diễn y theo x là y = $\frac{1}{4}$x.

Chọn đáp án C.

III. Vận dụng

Câu 1. Biết ba cạnh của một tam giác tỉ lệ thuận với 3, 4, 5 và chu vi của nó là 48 cm. Tính độ dài cạnh bé nhất của tam giác đó.

A. 20 cm;

B. 12 cm;

C. 16 cm;

D. 18 cm.

Hướng dẫn giải

Đáp án: B

Giải thích:

Gọi độ dài 3 cạnh của tam giác lần lượt là x, y, z.

Theo đề bài ta có x + y + z = 48 và $\frac{x}{3}$ = $\frac{y}{4}$ = $\frac{z}{5}$.

Áp dụng tính chất dãy tỉ số bằng nhau ta có

$\frac{\text{x}}{3}=\frac{y}{4}=\frac{z}{5}$ = $\frac{\text{x}+\text{y}+\text{z}}{3+4+5}$ = $\frac{48}{12}$ = 4.

Như vậy x = 4.3 = 12 cm;

y = 4.4 = 16 cm;

z = 4.5 = 20 cm.

Vậy độ dài cạnh bé nhất của tam giác là 12 cm. Chọn đáp án B.

Câu 2. Hai thanh sắt có thể tích lần lượt là 23 cm³ và 19 cm³. Thanh thứ nhất nặng hơn thanh thứ hai 56 gam. Thanh thứ nhất nặng

A. 368g;

B. 232g;

C. 312g;

D. 322g.

Hướng dẫn giải

Đáp án: D

Giải thích:

Do hai thanh sắt đồng chất nên khối lượng 2 thanh sắt tỉ lệ thuận với thể tích của nó. Gọi khối lượng hai thanh sắt lần lượt là x (g) và y (g).

Theo đề bài ta có x – y = 56 và $\frac{\text{x}}{\text{23}}$ = $\frac{\text{y}}{\text{19}}$.

Áp dụng tính chất dãy tỉ số bằng nhau:

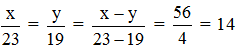
Như vậy x = 14.23 = 322

Vậy thanh sắt thứ nhất nặng 322 gam. Chọn đáp án D.

Câu 3. Để chuẩn bị làm thí nghiệm, cô giáo chia 2 lít hóa chất thành ba phần tỉ lệ thuận với 2, 3, 5 và đựng trong ba chiếc lọ. Hỏi chiếc lọ đựng nhiều hóa chất nhất chứa bao nhiêu lít hóa chất đó.

A. 0,4 lít;

B. 1 lít ;

C. 0,6 lít;

D. 1,2 lít .

Hướng dẫn giải

Đáp án: B

Giải thích:

Vậy lọ đựng nhiều hóa chất nhất chứa 1 lít hóa chất. Chọn đáp án B.

Xem thêm các bài trắc nghiệm Toán 7 Kết nối tri thức hay, chi tiết khác:

Trắc nghiệm Tính chất của dãy tỉ số bằng nhau

Trắc nghiệm Đại lượng tỉ lệ thuận

Trắc nghiệm Đại lượng tỉ lệ nghịch

Trắc nghiệm Biểu thức đại số

Trắc nghiệm Đa thức một biến