Bài tập Toán lớp 7 Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
A. Bài tập Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
A.1 Bài tập tự luận
Bài 1. Tính diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác biết, đáy của nó là tam giác vuông và các kích thước như hình vẽ (đơn vị của các cạnh là cm).
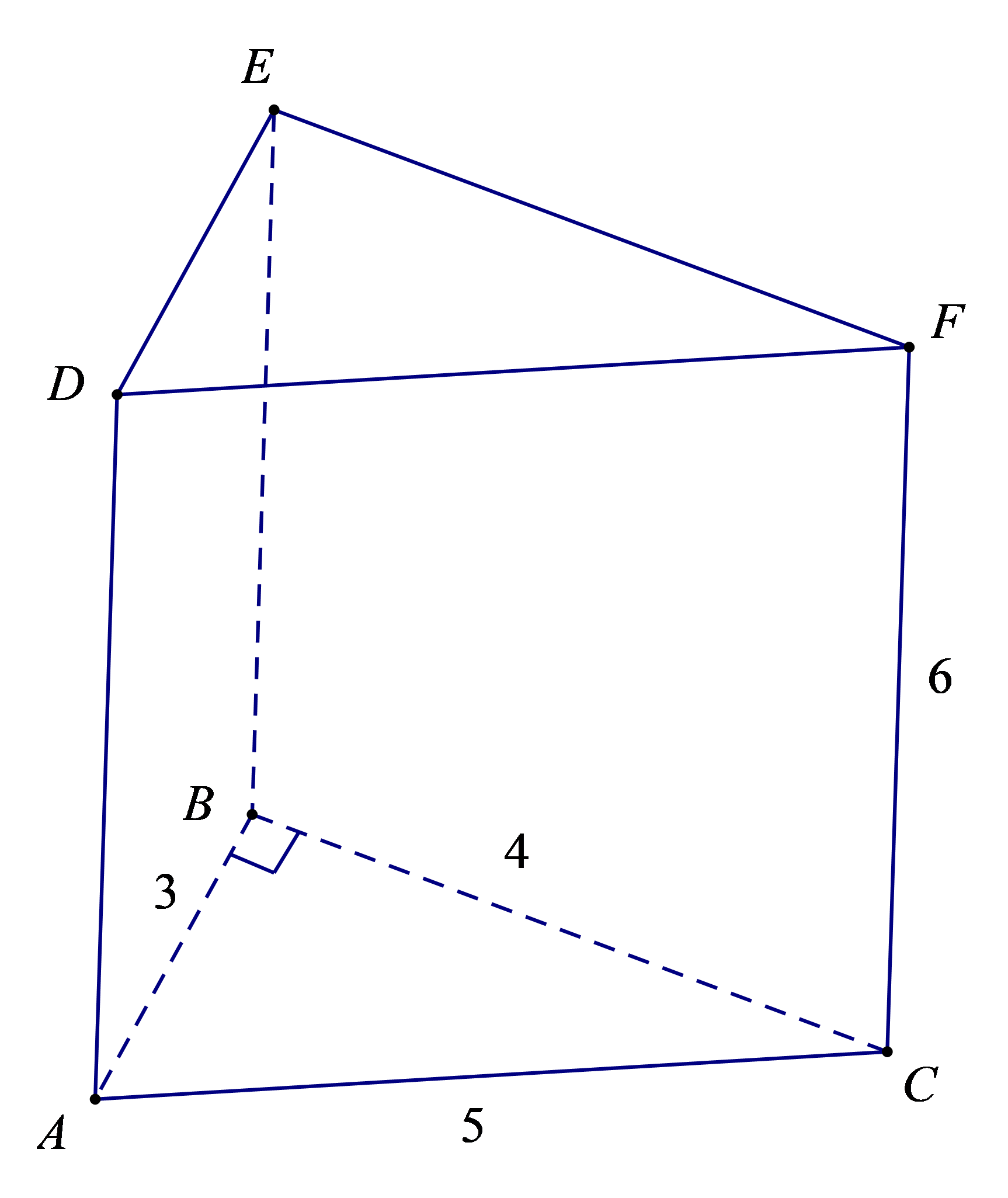
Hướng dẫn giải
Ta tính chu vi đáy là tam giác ABC: C = 3 + 4 + 5 = 12 (cm), chiều cao h = 6 cm.
Diện tích xung quanh của hình lăng trụ đứng tam giác ABC.DEF là:
Sxq = C . h = 12 . 6 = 72 (cm2).
Ta tính diện tích đáy (cm2).
Thể tích của hình lăng trụ đứng tam giác ABC.DEF là:
V = S.h = 6 . 6 = 36 (cm3).
Bài 2. Tính diện tích xung quanh và thể tích của lăng trụ đứng tứ giác, biết đáy của nó là hình chữ nhật (độ dài các cạnh đơn vị cm).
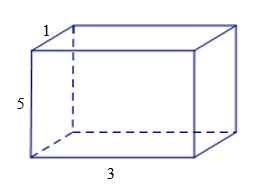
Hướng dẫn giải
Ta tính chu vi đáy C = 2(1 + 3 ) = 8 (cm), chiều cao h = 5 cm
Diện tích của hình lăng trụ đứng tứ giác này là: Sxq = C . h = 8 . 5 = 40 (cm2).
Ta tính diện tích đáy S = 1 . 3 = 3 (cm2)
Thể tích hình lăng trụ đứng tứ giác là: V = S . h = 3 . 5 = 15 (cm3).
A.2 Bài tập trắc nghiệm
Câu 1. Số cạnh của hình lăng trụ đứng tam giác là?
A. 9 cạnh;
B. 8 cạnh;
C. 5 cạnh;
D. 6 cạnh.
Hướng dẫn giải
Đáp án đúng là: A
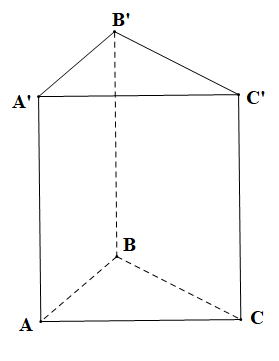
Lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh.
Câu 2. Thể tích hình lăng trụ đứng tứ giác có các kích thước như hình vẽ dưới đây là?
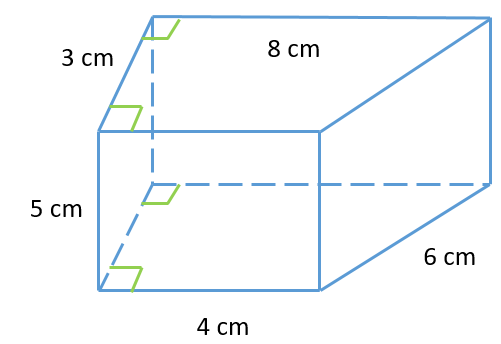
A. V = 80 cm3;
B. V = 18 cm3;
C. V = 19 cm3;
D. V = 90 cm3.
Hướng dẫn giải
Đáp án đúng là: D
Hai mặt đáy của hình lăng trụ đứng tứ giác là hai hình thang bằng nhau nên, diện tích một mặt đáy là: (cm2)
Thể tích hình lăng trụ đứng tứ giác là: V = 18 . 5 = 90 (cm3)
Vậy thể tích hình lăng trụ đứng tam giác là V = 90 cm3.
Câu 3. Cho hình lăng trụ đứng tam giác với hai đáy là hai tam giác và các kích thước như hình vẽ.
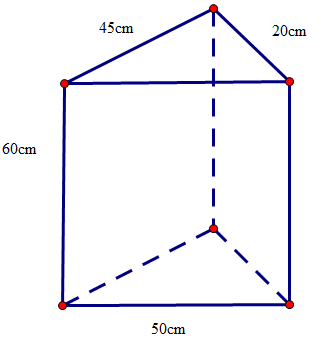
Diện tích xung quanh của hình lăng trụ đứng tam giác đó bằng?
A. 7 200 cm2;
B. 6 900 cm2;
C. 6 250 cm2;
D. 7 900 cm2.
Hướng dẫn giải
Đáp án đúng là: B
Diện tích xung quanh của hình lăng trụ đứng tam giác đó là:
Sxq = (45 + 20 + 50) . 60 = 6 900 (cm2)
Vậy diện tích xung quanh của hình lăng trụ đứng tam giác là Sxq = 6 900 cm2.
B. Lý thuyết Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
1. Hình lăng trụ đứng tam giác
– Hình lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh.
– Hai mặt đáy cùng là tam giác và nằm trong hai mặt phẳng song song với nhau; Mỗi mặt bên là hình chữ nhật;
– Các cạnh bên bằng nhau;
– Chiều cao của hình lăng trụ đứng tam giác là độ dài cạnh bên.
Ví dụ:
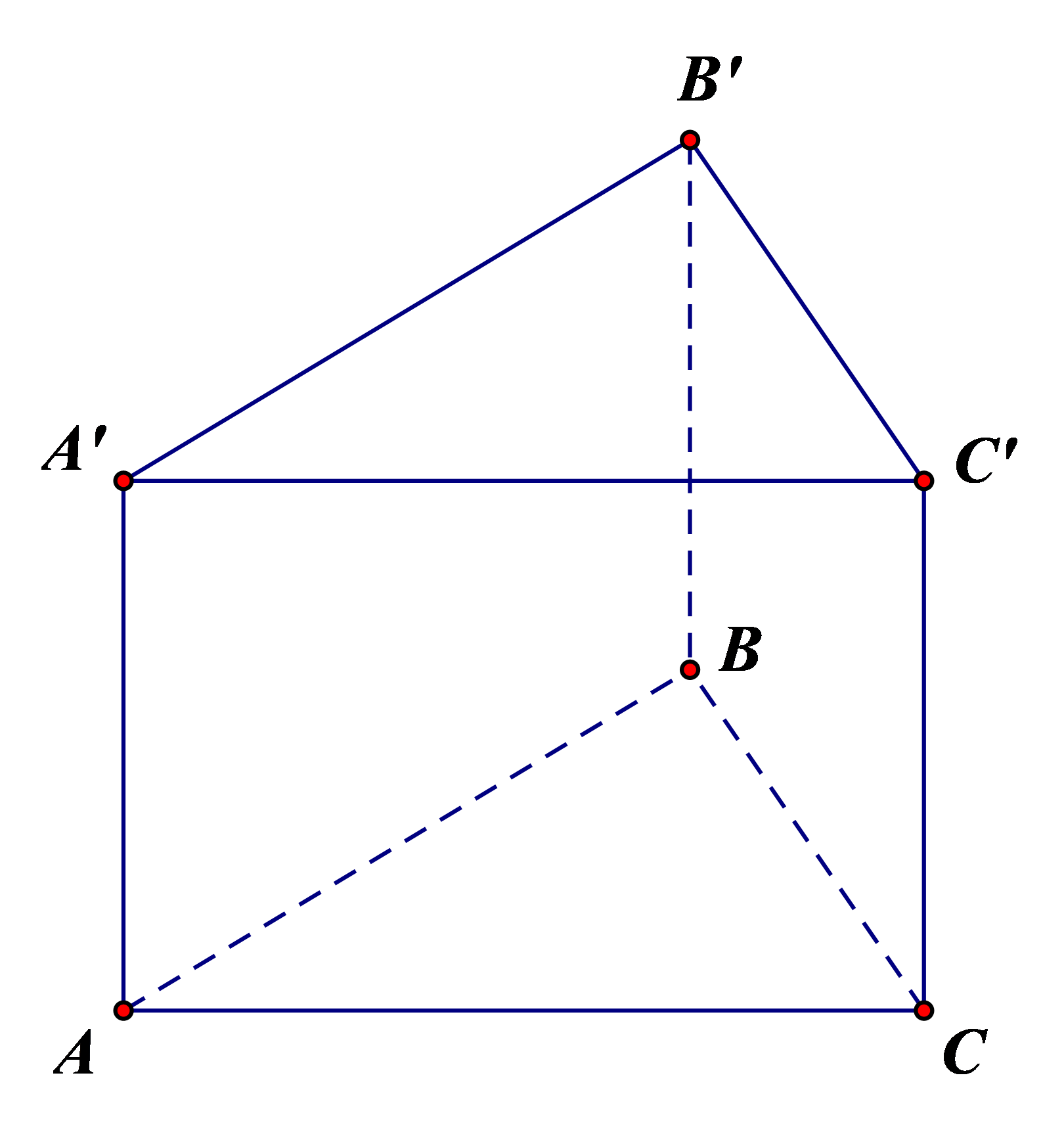
Hình lăng trụ đứng tam giác ABC.A’B’C’ có:
– Đáy dưới là tam giác ABC, đáy trên là tam giác A’B’C’;
Các mặt bên là các hình chữ nhật: AA’B’B, BB’C’C, CC’A’A;
– Các cạnh:
+ Cạnh đáy: AB, BC, CA, A’B’, B’C’, C’A’
+ Cạnh bên: AA’, BB’, CC’;
– Các đỉnh: A, B, C, A’, B’, C’.
– Chiều cao là độ dài một cạnh bên: AA’ hoặc BB’ hoặc CC’.
2. Hình lăng trụ đứng tứ giác
– Lăng trụ đứng tứ giác có 6 mặt, 12 cạnh, 8 đỉnh.
– Hai mặt đáy cùng là tứ giác và song song với nhau. Mỗi mặt bên là hình chữ nhật.
– Các cạnh bên bằng nhau.
– Chiều cao của hình lăng trụ đứng tứ giác là độ dài một cạnh bên.
Ví dụ:
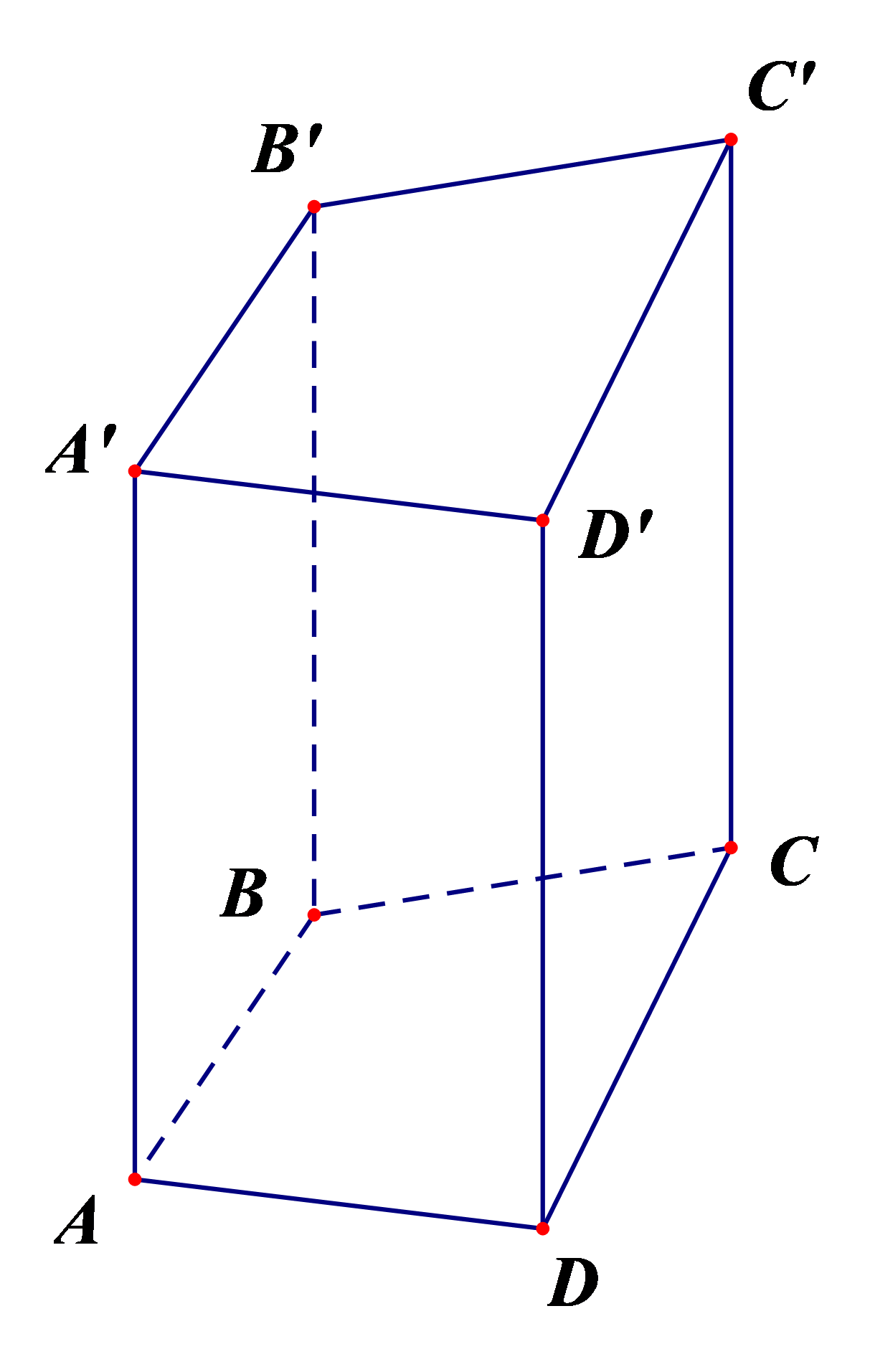
Hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ có:
– Đáy dưới là tứ giác ABCD, đáy trên là tứ giác A’B’C’D’;
Các mặt bên là các hình chữ nhật: AA’B’B, BB’C’C, CC’D’D, DD’A’A;
– Các cạnh:
+ Cạnh đáy: AB, BC, CD, DA, A’B’, B’C’, C’D’, D’A’
+ Các cạnh bên: AA’, BB’, CC’, DD’ bằng nhau.
– Các đỉnh: A, B, C, D, A’, B’, C’, D’.
– Chiều cao là độ dài một cạnh bên: AA’ hoặc BB’ hoặc CC’ hoặc DD’.
Chú ý: Hình hộp chữ nhật và hình lập phương cũng là lăng trụ đứng tứ giác.
3. Thể tích và diện tích xung quanh của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác
– Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.
Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tứ giác.
– Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.
Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tam giác.
– Diện tích xung quanh của hình lăng trụ đứng tam giác hay hình lăng trụ đứng tứ giác bằng chu vi đáy nhân với chiều cao.
Tức là Sxq = C . h, trong đó Sxq là diện tích xung quanh, C là chu vi đáy, h là chiều cao của hình lăng trụ đứng tam giác hay của hình lăng trụ đứng tứ giác.
Ví dụ:

a) Cho hình lăng trụ đứng tam giác ABC.A’B’C’.
Sxq = C . h, trong đó C là chu vi của tam giác ABC (hoặc tam giác A’B’C’), h là độ dài cạnh bên AA’ (hoặc BB, hoặc CC’).
V = S . h, trong đó S là diện tích tam giác ABC (hoặc A’B’C’), h là độ dài cạnh bên AA’ (hoặc BB’ hoặc CC’).
b) Cho hình lăng trụ đứng tứ giác ABCD.A’B’C’D’:
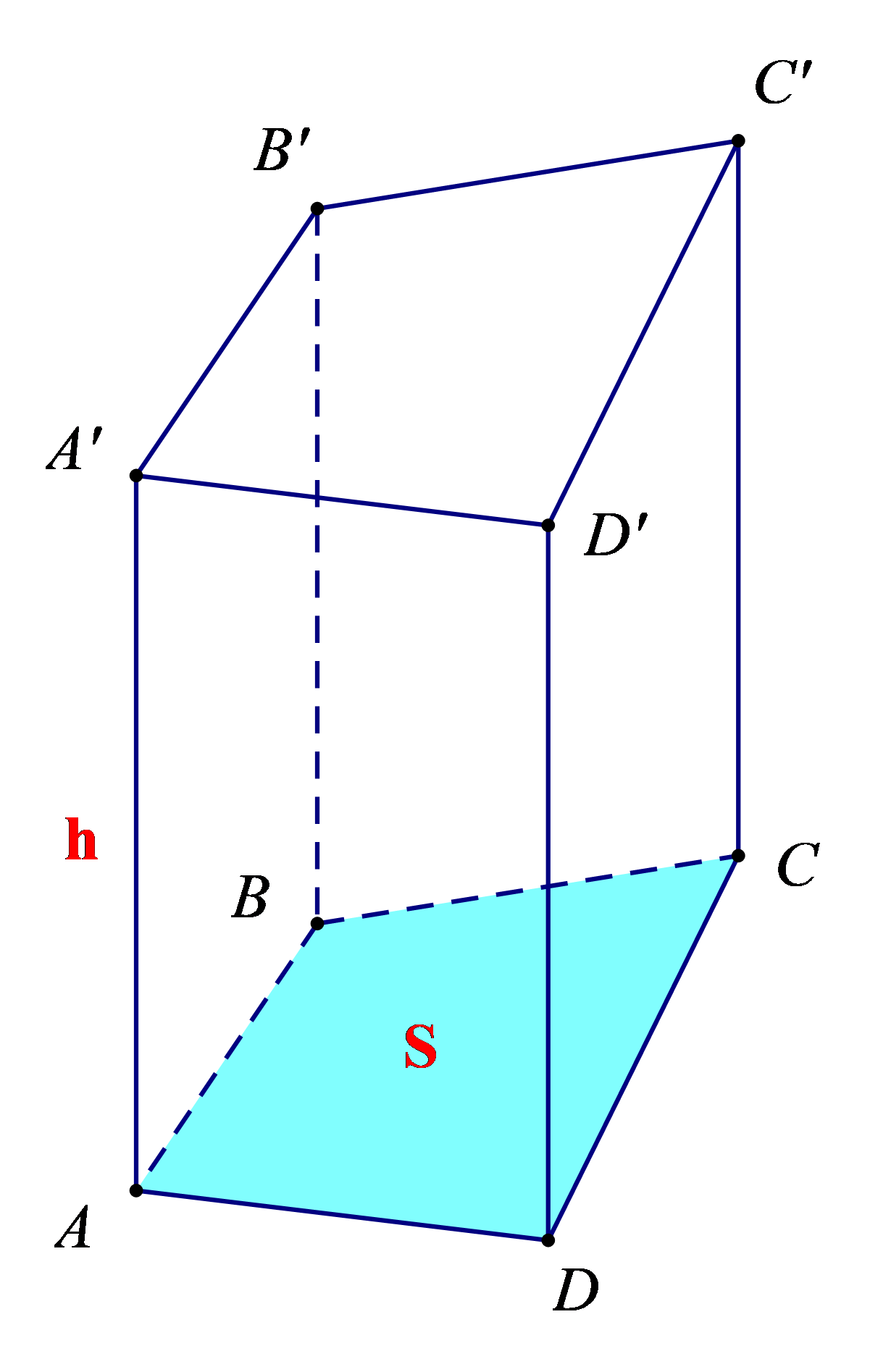
Sxq = C . h, trong đó C là chu vi của tứ giác ABCD (hoặc tứ giác A’B’C’D’), h là độ dài cạnh bên AA’ (hoặc BB, hoặc CC’, hoặc DD’).
V = S . h, trong đó S là diện tích tứ giác ABCD (hoặc A’B’C’D’), h là độ dài cạnh bên AA’ (hoặc BB’ hoặc CC’, hoặc DD’).