Bộ 15 Đề thi Toán lớp 11 Giữa kì 1 năm 2022 – 2023

Bộ Đề thi Toán lớp 11 Giữa kì 1 năm 2022 – 2023 (15 đề) – Đề 1

Phòng Giáo dục và Đào tạo …..

Đề khảo sát chất lượng Giữa kì 1

Năm học 2022 – 2023

Môn: Toán 11

Thời gian làm bài: 90 phút

Đề số 1

Câu 1. Tập xác định của hàm số \(y = \frac{{\cot x}}{{\cos x – 1}}\)là

A. \(\mathbb{R}\backslash \left\{ {k\frac{\pi }{2},k \in Z} \right\}\)

B. \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in Z} \right\}\)

C. \(\mathbb{R}\backslash \left\{ {k\pi ,k \in Z} \right\}\) 

D. \(\mathbb{R}\)

Câu 2. Trong mặt phẳng tọa độ \[Oxy\], cho điểm \[M\left( {1;1} \right).\] Hỏi điểm nào sau đây là ảnh của điểm \[M\] qua phép quay tâm\[O\left( {0;0} \right)\] , góc quay \[{45^0}\] ?

A. \[M’\left( {0;\sqrt 2 } \right)\].   

B. \[M’\left( {\sqrt 2 ;0} \right)\].

C. \[M’\left( {0;1} \right)\]. 

D. \[M’\left( {1; – 1} \right)\].

Câu 3 :Hàm số \(y = \sin 2x\) đồng biến trên khoảng nào trong các khoảng sau?

A. \(\left( {0;\frac{\pi }{4}} \right)\).

B. \(\left( {\frac{\pi }{2};\pi } \right)\). 

C. \(\left( {\pi ;\frac{{3\pi }}{2}} \right)\).

D. \(\left( {\frac{{3\pi }}{2};2\pi } \right)\).

Câu 4.  Gọi  là hình ảnh của \(d\) qua tâm \(I\) góc quay \(\varphi \) (biết \(I\) không nằm trên \(d\)), đường thẳng  song với \(d\) khi:

A. \(\varphi  = \frac{\pi }{3}\) .

B. \(\varphi  = \frac{\pi }{6}\).

C. \(\varphi  = \frac{{2\pi }}{3}\).   

D. \(\varphi  =  – \pi \)

Câu 5.Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. \(y =  – \sin x\).   

B. \(y = \cos x – \sin x\).

C. \(y = \cos x + {\sin ^2}x\).

D. \(y = \cos x\sin x\)

Câu 6. Trong mặt phẳng tọa độ \[Oxy\], cho đường tròn \(\left( C \right):\,{x^2} + {y^2} + 6x + 5 = 0\). Tìm ảnh đường tròn \(\left( {C’} \right)\) của \(\left( C \right)\) qua \({Q_{\left( {O,{{90}^0}} \right)}}\).

A. \({x^2} + {\left( {y – 3} \right)^2} = 4\).   

B. \(\left( C \right):\,{x^2} + {y^2} + 6y – 6 = 0\).  

C. \({x^2} + {\left( {y + 3} \right)^2} = 4\).

D. \(\left( C \right):\,{x^2} + {y^2} + 6x – 5 = 0\).

Câu 7. Một tổ học sinh có 5 nam và 5 nữ xếp thành một hàng dọc thì số các cách xếp khác nhau là:

A 25       

B. 10         

C. 10!     

D. 40

Câu 8. Cho hình vuông \(ABCD\) tâm \(I\). Gọi \(M,N\) lần lượt là trung điểm \(AD,DC\). Phép tịnh tiến theo vectơ nào sau đây biến tam giác \(AMI\) thành \(INC\)

A. \(\overrightarrow {AM} \). 

B. \(\overrightarrow {IN} \).   

C. \(\overrightarrow {AC} \).

D. \(\overrightarrow {MN} \).

Câu 9: Tìm chu kì T của hàm số \(y = 2{\sin ^2}x + 3{\cos ^2}3x\).

A. \(T = \pi \).         

B. \(T = 2\pi \).     

C. \(T = 3\pi \).     

D. \(T = \frac{\pi }{3}\).

Câu 10. Có 5 học sinh nam và 3 học sinh nữ xếp thành một hàng dọc. Hỏi có bao nhiêu cách xếp để 2 học sinh nam xen giữa 3 học sinh nữ? (đổi 2 học sinh bất kì được cách mới)

A. 2880           

B. 5760           

C. 1440         

D. 4320

Câu 11. Trong mặt phẳng tọa độ\[Oxy\], cho hai đường thẳng \(d:2x – 3y + 3 = 0\) và \(d’:2x – 3y – 5 = 0\). Tìm tọa độ \(\overrightarrow v \) có phương vuông góc với \(d\) và \({T_{\overrightarrow v }}\) biến đường thẳng \(d\) thành \(d’\).

 A. \(\overrightarrow v  = \left( {\frac{{ – 6}}{{13}};\frac{4}{{13}}} \right)\) .

B. \(\overrightarrow v  = \left( {\frac{{ – 1}}{{13}};\frac{2}{{13}}} \right)\) . 

C. \(\overrightarrow v  = \left( {\frac{{ – 16}}{{13}};\frac{{ – 24}}{{13}}} \right)\).

D. \(\overrightarrow v  = \left( {\frac{{16}}{{13}};\frac{{ – 24}}{{13}}} \right)\).

Câu 12. Gọi M; m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = 8{\sin ^2}x + 3\cos 2x\]. Tính Tính \[P = 2M – {m^2}\].

A. 1           

B. 2

C. 112         

D. 130

Câu 13. Nếu bốn số hạng đầu của một hàng trong tam giác Pascal được ghi lại là:

            1          16        120      560

Khi đó 4 số hạng đầu của hàng kế tiếp là:

A. 1         32         360         1680       

B. 1         18         123         564

C. 1         17         137         697         

D. 1         17         136         680

Câu 14. Có 3 tem thư khác nhau và 6 bì thư khác nhau. Người ta muốn chọn từ đó ra 3 tem thư, 3 bì thư và dán 3 tem thư đó lên 3 bì thư đã chọn, mỗi bì thư chỉ dán 1 tem thư. Hỏi có bao nhiêu cách làm như vậy?

 A. 200       

B. 30             

C. 300   

D. 120

Câu 15. Hình gồm hai đường thẳng \[d\] và \[d’\] vuông góc với nhau đó có mấy trục đối xứng?

A. \[0\].     

B. \[2\].       

C. \[4\].     

D. Vô số

Câu 16. Có bao nhiêu điểm biến thành chính nó qua phép quay tâm \[O\], góc quay \[\alpha  \ne k2\pi ,\,k \in \mathbb{Z}.\]

A. Không có.     

B. Một.         

C. Hai.         

D. Vô số.

Câu 17.  Với giá trị nào của \(x\) thì giá trị của các hàm số \(y = \sin 3x\) và \(y = \sin x\) bằng nhau?

A. \(\left[ \begin{array}{l}x = k2\pi \\x = \frac{\pi }{4} + k2\pi \end{array} \right.\left( {k \in Z} \right).\)

B. \(\left[ \begin{array}{l}x = k\pi \\x = \frac{\pi }{4} + k\frac{\pi }{2}\end{array} \right.\left( {k \in Z} \right).\)

C. \(x = k\frac{\pi }{4}\,\left( {k \in Z} \right).\)   

D. \(x = k\frac{\pi }{2}\,\left( {k \in Z} \right).\)

Câu 18. Nghiệm của phương trình \(\sin x.\left( {2\cos x – \sqrt 3 } \right) = 0\) là:

A. \(\left[ \begin{array}{l}x = k\pi \\x =  \pm \frac{\pi }{6} + k2\pi \end{array} \right.\), \[k \in \mathbb{Z}\].

B. \(\left[ \begin{array}{l}x = k\pi \\x =  \pm \frac{\pi }{6} + k\pi \end{array} \right.\), \[k \in \mathbb{Z}\].

C. \(\left[ \begin{array}{l}x = k2\pi \\x =  \pm \frac{\pi }{3} + k2\pi \end{array} \right.\), \[k \in \mathbb{Z}\].   

D. \(x =  \pm \frac{\pi }{6} + k2\pi \), \[k \in \mathbb{Z}\].

Câu 19. Trong mặt phẳng \[Oxy\], cho điểm \[M\left( {2;3} \right)\]. Hỏi \[M\] là ảnh của điểm nào trong các điểm sau qua phép đối xứng trục\[Oy\]?

A. \[\left( {3;2} \right)\].

B. \[\left( {2;–3} \right)\].

C. \[\left( {3;–2} \right)\].

D. \[\left( {–2;3} \right)\]

Câu 20. Từ A đến B có 3 con đường, từ B đến C có 4 con đường. Hỏi có bao nhiêu cách chọn đường từ A đến C (qua B) và trở về C đến A (qua B) và không đi lại các con đường đã đi rồi?

A. 72         

B. 132     

C. 18  

D. 23

Câu 21. Giải phương trình \[8\cot 2x = \frac{{\left( {{{\cos }^2}x – {{\sin }^2}x} \right).\sin 2x}}{{{{\cos }^6}x + {{\sin }^6}x}}\].

A. \[x =  – \frac{\pi }{4} + k\pi \].

B. \[x =  \pm \frac{\pi }{4} + \frac{{k\pi }}{2}\]. 

C. \[x = \frac{\pi }{4} + k\pi \].

D. \[x = \frac{\pi }{4} + \frac{{k\pi }}{2}\].

Câu 22. Nghiệm của phương trình lượng giác:  điều kiện  là:

A.      

B.           

C.         

 D.

Câu 23. Có bao nhiêu số tự nhiên gồm lẻ gồm 4 chữ số khác nhau? Đáp số của bài toán là

A. 2420.     

B. 3208.     

C. 2650.   

D. Kết quả khác.

Câu 24. Tìm số tự nhiên n thỏa \[A_n^3\] = 20n

A. n = 5       

B. n = 6     

C. n = 10       

D. n = 12

Câu 25. Tìm số hạng không chứa x trong khai triển của  \({\left( {{x^2} – \frac{2}{x}} \right)^{12}}\).

A. 126720     

B. –126720     

C. 7920   

D. –7920

II. Tự luận

  Câu 1.  Giải phương trình lượng giác \[\cot x – 1 = \frac{{\cos 2x}}{{1 + \tan x}} + {\sin ^2}x – \frac{1}{2}\sin 2x\]

Câu 2.Có 5 tem thư khác nhau và 6 bì thư khác nhau. Người ta muốn chọn từ đó ra 3 tem thư, 3 bì thư và dán 3 tem thư đó lên 3 bì thư đã chọn, mỗi bì thư chỉ dán 1 tem thư. Hỏi có bao nhiêu cách làm như vậy?

Bộ Đề thi Toán lớp 11 Giữa kì 1 năm 2022 – 2023 (15 đề) – Đề 2

Phòng Giáo dục và Đào tạo …..

Đề khảo sát chất lượng Giữa kì 1

Năm học 2022 – 2023

Môn: Toán 11

Thời gian làm bài: 90 phút

Đề số 2

Câu 1. Tập xác định của hàm số \(y = \tan \,\left( {2x – \frac{\pi }{3}} \right)\) là

A. \(x \ne \frac{\pi }{6} + \frac{{k\pi }}{2}\)   

B. \(x \ne \frac{{5\pi }}{{12}} + k\pi \)    

C. \(x \ne \frac{\pi }{2} + k\pi \) 

D. \(x \ne \frac{{5\pi }}{{12}} + k\frac{\pi }{2}\)

Câu 2.  Trong các mệnh đề sau mệnh đề nào đúng?

A. Phép đối xứng trục không có điểm nào biến thành chính nó.

B. Phép đối xứng trục có đúng một điểm biến thành chính nó.

C. Có phép đối xứng trục có hai điểm biến thành chính nó.

D. Có phép đối xứng trục có vô số điểm biến thành chính nó.

Câu 3. Trong khai triển \({\left( {2a – b} \right)^5}\), hệ số của số hạng thứ 3 bằng:

A. 80         

B. −10           

C. 10       

D. −80

Câu 4. Cho đường tròn \[\left( C \right)\]có tâm \[O\] và đường kính \[AB\]. Gọi \(\Delta \) là tiếp tuyến của \[\left( C \right)\] tại điểm \[A\]. Phép tịnh tiến theo vectơ \(\overrightarrow {AB} \) biến \(\Delta \) thành:

A. Đường kính của đường tròn \[\left( C \right)\] song song với \(\Delta \).

B. Tiếp tuyến của \[\left( C \right)\] tại điểm \[B\].

C. Tiếp tuyến của \[\left( C \right)\] song song với \[AB\].

D. Đường thẳng song song với \(\Delta \)và đi qua \[O\]

Câu 5.Trong mặt phẳng tọa độ \[Oxy\], cho \(\overrightarrow v  = \left( { – 4;2} \right)\) và đường thẳng \(\Delta ‘:2x + y – 5 = 0\). Hỏi \(\Delta ‘\) là ảnh của đường thẳng \(\Delta \) nào sau đây qua \({T_{\overrightarrow v }}.\)

A.\(\Delta :2x + y + 5 = 0\) .   

B. \(\Delta :2x + y – 9 = 0\).        

C. \(\Delta :2x + y – 15 = 0\).         

D. \(\Delta :2x + y – 11 = 0\).

Câu 6.Hàm số \(y = \sin x\)đồng biến trên:

A. Khoảng \[\left( {0;\pi } \right)\].                                                          

 B. Các khoảng \(\left( { – \frac{\pi }{4} + k2\pi ;\frac{\pi }{4} + k2\pi } \right)\), \[k \in \mathbb{Z}\].

C. Các khoảng \[\left( {\frac{\pi }{2} + k2\pi ;\pi  + k2\pi } \right)\], \[k \in \mathbb{Z}\].          

D. Khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\).

Câu 7. Từ các chữ số 0, 1, 2, 3, 4, 6, 8 lập được bao nhiêu số có ba chữ số khác nhau luôn có mặt chữ số 3?

A. 100             

B. 180               

C. 80         

D. 125

Câu 8.Trong mặt phẳng tọa độ \[Oxy\], cho điểm \(A\left( {3; – 3} \right)\). Tìm tọa độ diểm \(A’\) là ảnh của \(A\)qua phép tịnh tiến theo véctơ \(\vec v = \left( { – 1;3} \right)\).

A. \(A’\left( {2; – 6} \right)\).         

B. \(A’\left( {2;0} \right)\).   

C. \(A’\left( {4;0} \right)\).         

D. \(A’\left( { – 2;0} \right)\).

Câu 9:Cho hình lục giác đều \[ABCDE\] tâm\[O\] . Tìm ảnh của tam giác \[AOF\] qua phép quay tâm \[O\] góc quay \({120^0}\).

A.\(\Delta OAB\).     

B. \(\Delta BOC\).   

C. \(\Delta DOC\). 

D. \(\Delta EOD\).

Câu 10. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tạo độ?

A. \(y = \cot 4x\).         

B. \(y = \frac{{\sin x + 1}}{{\cos x}}\). 

C. \(y = {\tan ^2}x\).

D. \(y = \left| {\cot x} \right|\).

Câu 11:Tìm chu kì T của hàm số \[y = \tan 3\pi x\].

A. \[T = \frac{\pi }{3}\].     

B. \[T = \frac{4}{3}\]. 

C. \[T = \frac{{2\pi }}{3}\].   

D. \[T = \frac{1}{3}\].

Câu 12. Trong mặt phẳng \[Oxy\], cho điểm\[M\left( {2;3} \right)\]. Hỏi trong bốn điểm sau điểm nào là ảnh của \[M\] qua phép đối xứng trục \[Ox\]?

A. \[\left( {3;2} \right)\].   

B. \[\left( {2;–3} \right)\].

C. \[\left( {3;–2} \right)\].

D. \[\left( {–2;3} \right)\]

Câu 13. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số . Tính P= M- 2m²

A. 1           

B. 7         

C. 8     

D. 2

Câu 14. Nghiệm của phương trình  là

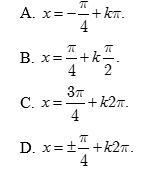
Câu 15. Một hộp có chứa 8 bóng đèn màu đỏ và 5 bóng đèn màu xanh. Số cách chọn được một bóng đèn trong hộp đó là:

A. 13     

B. 5           

C. 8         

D. 40

Câu 16. Phương trình \(\sin x = \frac{1}{2}\) có nghiệm thỏa \(\frac{{ – \pi }}{2} \le x \le \frac{\pi }{2}\) là:

A. \(x = \frac{{5\pi }}{6} + k2\pi \).

B. \(x = \frac{\pi }{6}\)..

C. \(x = \frac{\pi }{3} + k2\pi \).

D. \(x = \frac{\pi }{3}\).

Câu 17.  Phương trình:  có nghiệm là:.

A. \[x = \frac{\pi }{2} + k\pi \].   

B. .   

C. . 

D. Vô nghiệm.

Câu 18. Có bao nhiêu số là ước dương của và chia hết cho  ?

A. 30       

B. 150       

C. 60   

D. 120

Câu 19. Trong , phương trình  có tập nghiệm là

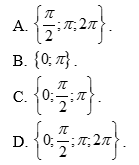
Câu 20. Một quán tạp hóa có 6 loại rượu, 4 loại bia và 3 loại nước ngọt. Ông Ba cần chọn mua đúng một loại đồ uống.

A. 13     

B. 72         

C. 30     

D. 42

Câu 21. Trong mặt phẳng tọa độ\[Oxy\], cho đường thẳng \(\Delta 😡 + 5y – 1 = 0\) và vectơ \(\overrightarrow v  = \left( {4;2} \right)\). Khi đó ảnh của đường thẳng \(\Delta \) qua phép tịnh tiến theo vectơ \(\overrightarrow v \) là

A.\(x + 5y – 15 = 0\) .   

B. \(x + 5y + 15 = 0\).     

C. \(x + 5y + 6 = 0\).   

D. \( – x – 5y + 7 = 0\).

Câu 22: Cho phương trình:  trong đó  là tham số. Để phương trình là vô nghiệm, thì các giá trị thích hợp của  là:

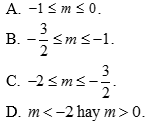
Câu 23: Trong mặt phẳng\[{\rm{Ox}}y\], ảnh của đường tròn: \[{\left( {x – 2} \right)^2} + {\left( {y – 1} \right)^2} = 16\]qua phép tịnh tiến theo vectơ  \[\overrightarrow v  = \left( {1;3} \right)\]là đường tròn có phương trình:

A. \[{\left( {x – 2} \right)^2} + {\left( {y – 1} \right)^2} = 16\].

B.\[{\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} = 16\].                                

C. \[{\left( {x – 3} \right)^2} + {\left( {y – 4} \right)^2} = 16\].  

D. \[{\left( {x + 3} \right)^2} + {\left( {y + 4} \right)^2} = 16\].

Câu 24: Trong mặt phẳng \[Oxy\]  cho điểm \[M\left( {2;3} \right)\] . Hỏi trong bốn điểm sau điểm nào là ảnh của \[M\]qua phép đối xứng trục \[Ox\]?

A. \[\left( {3;2} \right)\] .

B. \[\left( {2; – 3} \right)\] . 

C. \[\left( {3; – 2} \right)\] .  

D. \[\left( { – 2;3} \right)\] .

Câu 25 : Trong mặt phẳng Oxy, ảnh của điểm \(M\left( { – 6;1} \right)\)qua phép quay \({Q_{\left( {O,{{90}^o}} \right)}}\) là:

A.\(M’\left( { – 1; – 6} \right)\) . 

B. \(M’\left( {1;6} \right)\). 

C. \(M’\left( { – 6; – 1} \right)\).   

D. \(M’\left( {6;1} \right)\).

Bộ Đề thi Toán lớp 11 Giữa kì 1 năm 2022 – 2023 (15 đề) – Đề 3

Phòng Giáo dục và Đào tạo …..

Đề khảo sát chất lượng Giữa kì 1

Năm học 2022 – 2023

Môn: Toán 11

Thời gian làm bài: 90 phút

Đề số 3

Câu 1.  Tập xác định của hàm số \(y = \tan \,\left( {2x – \frac{\pi }{3}} \right)\) là

A. \(x \ne \frac{\pi }{6} + \frac{{k\pi }}{2}\).

B. \(x \ne \frac{{5\pi }}{{12}} + k\pi \).

C. \(x \ne \frac{\pi }{2} + k\pi \).   

D. \(x \ne \frac{{5\pi }}{{12}} + k\frac{\pi }{2}\).

Câu 2: Với \(x \in \left( {\frac{{31\pi }}{4};\frac{{33\pi }}{4}} \right)\), mệnh đề nào sau đây là đúng?

A. Hàm số \(y = \cot x\) nghịch biến. 

B. Hàm số \(y = \tan x\) nghịch biến.

C. Hàm số \(y = \sin x\) đồng biến.

D. Hàm số \(y = \cos x\) nghịch biến.

Câu 3. Cho tập \(A = \left\{ {1;2;3;4;5;6;7} \right\}\). Từ tập A có thể lập được bao nhiêu số tự nhiên chẵn có 7 chữ số sao cho chữ số 1 đứng ở vị trí chính giữa?

A. 360     

B. 9375   

C. 3125 

D. 120

Câu 4. Trong khai triển \({\left( {x – y} \right)^{11}}\), hệ số của số hạng chứa \({x^8}{y^3}\) là:

A. \( – C_{11}^3\)

B. \(C_{11}^8\)

C. \(C_{11}^3\)   

D. \( – C_{11}^5\)

Câu 5:  Hình nào sau đây không có trục đối xứng?

A. Hình vuông.   

B. Hình tròn.     

C. Hình tam giác đều.

D. Hình thoi.

Câu 6. Giả sử \({T_{\overrightarrow v }}(M) = M’;{T_{\overrightarrow v }}(N) = N’\). Mệnh đề nào sau đây sai?

A. \(\overrightarrow {M’N’}  = \overrightarrow {MN} \).

B. \(\overrightarrow {MM’}  = \overrightarrow {NN’} \)

C.\(MM’ = NN’\). 

D. \(MNM’N’\) là hình bình hành.

Câu 7. Trong các hàm số sau hàm số nào là hàm số lẻ?

A. \(y = \cos x + {\sin ^2}x\). 

B. \(y = \sin x + \cos x\).

C. \(y =  – \cos x\).

D. \(y = \sin x.\cos 3x\).

Câu 8:   Tìm ảnh của đường thẳng \[d:5x – 3y + 15 = 0\] qua phép quay \[{Q_{\left( {O;{{90}^0}} \right)}}\].

A. \[d’:x + y + 15 = 0\]         

B. \[d’:3x + 5y + 5 = 0\]

C. \[d’:3x + y + 5 = 0\]       

D. \[d’:3x + 5y + 15 = 0\]

Câu 9. Có 8 quyển sách khác nhau và 6 quyển vở khác nhau. Số cách chọn một trong các quyển đó là:

A. 6         

B. 8       

C. 14   

D. 48

Câu 10.Trong mặt phẳng tọa độ \(Oxy\), tìm phương trình đường tròn \(\left( {C’} \right)\) là ảnh cảu đường tròn \(\left( C \right):{x^2} + {y^2} – 2{\rm{x}} + 4y – 1 = 0\) qua \({T_{\vec v}}\) với \(\vec v = \left( {1;2} \right)\).

A. \({\left( {x + 2} \right)^2} + {y^2} = \sqrt 6 \).

B. \({\left( {x – 2} \right)^2} + {y^2} = 6\).

C. \({x^2} + {y^2} – 2{\rm{x}} – 5 = 0\).   

D. \(2{x^2} + 2{y^2} – 8x + 4 = 0\).

Câu 11:Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

A. \[y = \sin x – x\].     

B. \[y = \cos x\].

C. \[y = x\sin x\].   

D. \[y = \frac{{{x^2} + 1}}{x}\].

Câu 12. Tìm chu kì Tcủa hàm số \[y = \cos 3x + \cos 5x\].

A. \(T = \pi \).     

B. \(T = 3\pi \).

C. \(T = 2\pi \).

D. \(T = 5\pi \).

Câu 13. Có bao nhiêu số có 4 chữ số khác nhau được tạo thành từ các số 1, 2, 3, 4, 5?

A. \({P_4}\) 

B. \({P_5}\)

C. \(A_5^4\)   

D. \(C_5^4\)

Câu 14: Cho 2 đường thẳng bất kì \[d\] và . Có bao nhiêu phép quay biến đường thẳng \[d\] thành đường thẳng ?

A. không có phép nào.

B. có 1 phép duy nhất.

C. chỉ có 2 phép. 

D. có vô phép số.

Câu 15. Hàm số \[y = 1 + 2{\rm{ }}{\cos ^2}x\] đạt giá trị nhỏ nhất tại \[x = {x_0}\]. Mệnh đề nào sau đây là đúng?

A. \[{x_0} = \pi  + k2\pi ,k \in \mathbb{Z}\].

B. \[{x_0} = \frac{\pi }{2} + {\rm{ }}k\pi ,k \in \mathbb{Z}\].

C. \[{x_0} = k2\pi ,k \in \mathbb{Z}\].

D. \[{x_0} = k\pi ,k \in \mathbb{Z}\].

Câu 16. Trong mặt phẳng Oxy. Phép đối xứng tâm  biến điểm  thành điểm:

Câu 17.  Bạn muốn mua một cây bút mực và một cây bút chì. Các cây bút mực có 8  màu khác nhau, các cây bút chì có 8 màu khác nhau. Bạn có số cách lựa chọn là:

A. 64 .   

B. 16 . 

C. 32 .   

D. 20 .

Câu 18.Trong mặt phẳng tọa độ \[Oxy\], cho các điểm  và . Phép quay tâm \[I\left( {x;y} \right)\] biến \[A\] thành  và \[B\] thành , ta có \[x + y\] bằng:

A. \[ – 1\].   

B. \[2\]       

C. \[1\]     

D. \[ – 3\]

Câu 19. Giải phương trình \[\frac{{1 + {{\sin }^2}x}}{{1 – {{\sin }^2}x}} – {\tan ^2}x = 4\].

A. \[x =  \pm \frac{\pi }{3} + k2\pi \].

B. \[x =  \pm \frac{\pi }{6} + k2\pi \].      

C. \[x =  \pm \frac{\pi }{3} + k\pi \]   

D. \[x =  \pm \frac{\pi }{6} + k\pi \].

Câu 20: Nghiệm của phương trình  2sin²x – 3sinx + 1 = 0 thỏa điều kiện

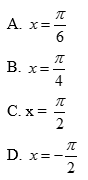
II. Tự luận

Câu 1. Trong một buổi giao lưu, có 5 học sinh trường X và 5 học sinh trường Y ngồi và o2 bàn đối diện nhau. Hỏi có bao nhiêu cách xếp sao cho 2 người ngồi đối diện và ngồi cạnh thì khác trường nhau.

Câu 2.Cho phương trình: . Tìm các nghiệm của phương trình thuộc khoảng 

Câu 3:Trong mặt phẳng tọa độ \[Oxy\], cho hai đường thẳng \(d:x + y – 1 = 0\) và \(d’:x + y – 5 = 0\). Phép tịnh tiến theo vectơ \(\overrightarrow u \) biến đường thẳng d thành d’. Khi đó, độ dài bé nhất của vectơ \(\overrightarrow u \)là bao nhiêu?