Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Bài tập trắc nghiệm tổ hợp và xác suất nâng cao có lời giải chi tiết
Câu 1. Cho 5 điểm đồng phẳng sao cho các đường thẳng đi qua các cặp điểm trong 5 điểm đó không có 2 đường thẳng nào song song, vuông góc hay trùng nhau. Qua mỗi điểm ta vẽ các đường vuông góc với tất cả các đường thẳng nối 2 điểm trong 4 điểm còn lại. Không kể 5 điểm đã cho số giao điểm của các đường thẳng vuông góc đó nhiều nhất là bao nhiêu?
A. 310 .
B. 330 .
C. 360 .
D. 325 .
Lời giải
Chọn A
Gọi 5 điểm đó là A, B, C, D, E
Có \(C_4^2 = 6\) đường thẳng không đi qua A nên từ A kẻ được 6 đường thẳng vuông góc với 6 đường thẳng đó. Tương tự từ B kẻ được 6 đường thẳng vuông góc với 6 đường thẳng không đi qua B. Đáng lẽ ra 2 nhóm đường thẳng này cắt nhau tại
6×6 =36 điểm ( Không kể A, B). Nhưng vì có \[C_3^2 = 3\] đường thẳng không đi qua 2 điểm A, B nên 3 đường thẳng vuông góc vẽ từ A và 3 đường thẳng vuông góc vẽ từ B đôi một song song với nhau nên số giao điểm của 2 nhóm đường thẳng vuông góc này chỉ còn 36 -3 = 33 điểm. Có \(C_5^2 = 10\) cách chọn các cặp điểm như vậy nên có 330 giao điểm của các đường thẳng vuông góc. Thế nhưng cứ mỗi 3 điểm như A, B, C thì 3 đường cao của tam giác này trong số các đường vuông góc đó lại đồng quy tại 1 điểm ( thay vì cắt nhau tại 3 điểm) nên số giao điểm giảm đi 2. Vì \(C_5^3 = 10\) tam giác như tam giác ABC nên số giao điểm giản đi 20. Vậy số giao điểm nhiều nhất của các đường thẳng vuông góc là 330-20=310.
Mở rộng: Bài này có thể tổng quát cho n điểm \((n > 2)\)
Câu 2. Từ các chữ số thuộc tập \(X = \{ 1;2;3;4;5;6;7\} \) có thể lập được bao nhiêu số tự nhiên chẵn gồm 5 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 9 .
A. 96 .
B. 144 .
C. 72 .
D. 120 .
Lời giải
Chọn A
Ta có nhận xét \(1 + 2 + 3 + 4 + 5 + 6 + 7 = 28\) là số khi chia cho 9 có dư là 1 .
Vậy khi đó để chọn ra số tự nhiên có 5 chữ số chia hết cho 9 ta cần loại đi trong tập X hai chữ số có tổng khi chia cho 9 dư là 1 .
Do đó có hai trường hợp loại đi hai số có tổng chia cho 9 dư 1 là \(\{ 3;7\} ;\{ 4;6\} \)
Khi loại đi cặp \(\{ 3;7\} \) ta có:
+ Chọn số cho vị trí hàng đơn vị có 3 cách.
+ Chọn số cho các vị trí còn lại có 4 ! cách.
Trường hợp này có \(3.4! = 72\) số.
Khi loại đi cặp \(\{ 4;6\} \) ta có:
+ Chọn số cho vị trí hàng đơn vị có 1 cách.
+ Chọn số cho các vị trí còn lại có 4 ! cách.
Trường hợp này có \(4! = 24\) số.
Vậy có tất cả \(72 + 24 = 96\) số thỏa mãn yêu cầu.
Câu 3. (THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018) Một khối lập phương có độ dài cạnh là 2cm được chia thành 8 khối lập phương cạnh 1cm. Hỏi có bao nhiêu tam giác được tạo thành từ các đỉnh của khối lập phương cạnh 1cm.
A. 2876 .
B. 2898 .
C. 2915 .
D. 2012 .
Lời giải
Chọn D
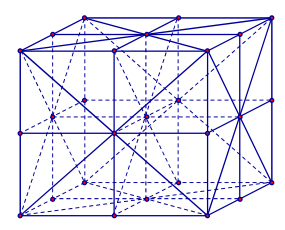
Có tất cả 27 điểm.
Chọn 3 điểm trong 27 có \(C_{27}^3 = 2925\).
Có tất cả \((8.2 + 6.2 + 4.2 + 4 + 3 + 2 + 2 + 2) = 49\) bộ ba điểm thẳng hàng.
Vậy có \(2925 – 49 = 2876\) tam giác.
Câu 4. Cho tập \(A = \{ 0,1,2,3,4,5,6,7,8,9\} \).Từ các phần tử của tập A có thể lập được bao nhiêu số có 6 chữ số đôi một khác nhau mà trong đó hai số chẵn không thể đứng cạnh nhau?
A.26880.
B. 27360 .
C. 34200 .
D. 37800 .
Lời giải
Chọn D
Giả sử số có 6 chữ số thỏa đề bài có dạng \(M = \overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} \).
Nhận xét : Trong các vị trí \({a_1},{a_2},{a_3},{a_4},{a_5},{a_6}\) có tối đa 3 chữ số là số chẵn được lấy từ tập A.
TH1 : Số M chỉ chứa 1 chữ số chã̃n
\( + {a_1}\) chẵn : \({a_1}\) có 4 cách chọn
Các vị trí \({a_2},{a_3},..,{a_5}\) là số lẻ nên có 5 ! cách xếp
H này có : \(4.5! = 480\) cách chọn.
\( + {a_1}\) lẻ : \({a_1}\) có 5 cách chọn
Chọn một chữ số chẵn và 4 chữ số lẻ và xếp chúng ở 5 vị trí \({a_2},{a_3},..,{a_5}\) như sau \(C_5^1 \cdot C_4^4.5\) ! cách
TH này có : \(5 \cdot C_5^1 \cdot C_4^4 \cdot 5! = 3000\) cách chọn.
TH2: Số M có chứa 2 chữ số chẵn .
\( + {a_1}\) chã̃n : \({a_1}\) có 4 cách chọn
Vị trí \({a_2}\) là số lẻ nên \({a_2}\) có 5 cách chọn .
Chọn một chữ số chẵn và 3 số lẻ và xếp chúng vào 4 vị trí còn lại có \(C_4^1 \cdot C_4^3 \cdot 4\) ! cách
TH này có : \(4.5 \cdot C_4^1 \cdot C_4^3 \cdot 4! = 7680\) cách chọn.
\( + {a_1}\) lẻ : \({a_1}\) có 5 cách chọn
Ỏ các vị trí \({a_2},{a_3},..,{a_5}\) có 3 chữ số lẻ, ta tạo được 4 vách ngăn, chọn hai chữ số chẵn và đặt vào 2 trong 4 vách ngăn đó,chọn 3 chữ số lẻ trong 4 số lẻ đặt ở 3 vị trí còn lại có \(C_5^2 \cdot C_4^2 \cdot 2! \cdot C_4^3 \cdot 3\) ! cách.
TH này có \(5 \cdot C_5^2 \cdot C_4^2 \cdot 2! \cdot C_4^3 \cdot 3! = 14400\) cách chọn.
TH3: Số M có chứa 3 chữ số chã̃n .
\( + {a_1}\) chẵn : \({a_1}\) có 4 cách chọn
Vị trí \({a_2}\) lẻ nên \({a_2}\) có 5 cách chọn
Ở các vị trí \({a_3},{a_4},{a_5},{a_6}\) có 2 chữ số lẻ , ta tạo được 3 vách ngăn, chọn hai chữ số chẵn và đặt vào 2 trong 3 vách ngăn đó,chọn 2 chữ số lẻ trong 4 số lẻ đặt ở 2 vị trí còn lại có \(C_4^2 \cdot C_3^2 \cdot 2! \cdot C_4^2 \cdot 2\) ! cách.
TH này có \(4 \cdot 5 \cdot C_4^2 \cdot C_3^2 \cdot 2! \cdot C_4^2 \cdot 2! = 8640\) cách chọn.
\( + {a_1}\) lẻ : \({a_1}\) có 5 cách chọn
Ỏ các vị trí \({a_2},{a_3},..,{a_5}\) có 2 chữ số lẻ, ta tạo được 3 vách ngăn, chọn ba chữ số chẵn và đặt vào 3 vách ngăn đó,chọn 2 chữ số lẻ trong 4 số lẻ đặt ở 2 vị trí còn lại có \(C_5^3 \cdot 3! \cdot C_4^2 \cdot 2\) ! cách.
TH này có \(5 \cdot C_5^3 \cdot 3! \cdot C_4^2 \cdot 2! = 3600\) cách chọn
Vậy có : \(480 + 3000 + 7680 + 14400 + 8640 + 3600 = 37800\) cách chọn thỏa yêu cầu bài toán.
Câu 5. Cho đa giác đều 20 cạnh nội tiếp đường tròn (O). Xác định số hình thang có 4 đỉnh là các đỉnh của đa giác đều.
A. 765
B. 720
C. 810
D. 315
Lời giải
Hình thang luôn có trục đối xứng đi qua tâm nên ta chỉ xét trục đối xứng vuông góc với hai đáy của hình thang trong hai trường hợp
Th1: Trục đối xứng của hình thang đi qua hai đỉnh của đa giác đều .
Chọn một trục đối xứng có 10 cách
Mỗi trục đối xứng như vậy ta có \(C_9^2\) cách chọn các đỉnh của hình thang nhận trục đối xứng đó
Suy ra \(10 \cdot C_9^2 = 360\) hình thang có trục đối xứng đi qua các đỉnh đa diện
Th2: Trục đối xứng không đi qua đỉnh của đa giác đều
Chọn một trục đối xứng như vậy ta có 10 cách
Mỗi trục đối xứng như vậy ta có \(C_{10}^2\) cách chọn các đỉnh của hình thang nhận trục đối xứng đó
Suy ra \(10 \cdot C_{10}^2 = 450\) hình thang có trục đối xứng không qua các đỉnh của đa giác đều
Lại có \(C_{10}^2 = 45\) hình chữ nhật là hình thang có hai trục đối xứng nên số hình thang thỏa mãn yêu cầu bài toán là \(360 + 450 – 45 = 765\)
Câu 6. Hỏi có tất cả bao nhiêu số tự nhiên chia hết cho 9 mà mỗi số 2011 chữ số và trong đó có ít nhất hai chữ số 9 .
A. \({10^{2010}} – {16151.9^{2008}}\).
B. \({10^{2010}} – {16153.9^{2008}}\)
C. \({10^{2010}} – {16148.9^{2008}}\)
D. \({10^{2010}} – {16161.9^{2008}}\).
Lời giải
Chọn D
Đặt \({A_1} = \{ 0;9\} ;{A_2} = \{ 1\} ;{A_3} = \{ 2\} ;{A_4} = \{ 3\} ;{A_5} = \{ 4\} ;{A_6} = \{ 5\} ;{A_7} = \{ 6\} ;{A_8} = \{ 7\} ;{A_9} = \{ 8\} \)
Gọi số cần tìm là \(n = \overline {{a_1}{a_2} \ldots {a_{2010}}{a_{2011}}} \left( {{a_1} \ne 0} \right)\)
+ Xét các số tự nhiên chia hết cho 9 , gồm 2011 chữ số:
Mỗi vị trí từ \({a_2}\) đến \({a_{2011}}\) đều có 10 cách chọn
\({a_1}\) phụ thuộc vào tổng \(\left( {{a_2} + {a_3} + \ldots + {a_{2011}}} \right)\) nên có 1 cách chọn
Vậy có \({10^{2010}}\) số
+ Xét các số tự nhiên chia hết cho 9, gồm 2011 chữ số nhưng không có mặt chữ số 9 :
\({a_1}\) có 8 cách chọn
Từ \({a_2}\) đến \({a_{2010}}\), mỗi vị trí đều có 9 cách chọn
\({a_{2011}}\) có 1 cách chọn
Vậy có \({8.9^{2009}}\) số.
+ Xét các số tự nhiên chia hết cho 9 , gồm 2011 chữ số trong đó có đúng 1 chữ số 9 :
+ Trường hợp \({a_1} = 9\) ta có:
Từ \({a_2}\) đến \({a_{2010}}\), mỗi vị trí đều có 9 cách chọn
\({a_{2011}}\) có 1 cách chọn
Do đó có \({9^{2009}}\) số
+ Trường hợp \({a_1} \ne 9\) ta có:
\({a_1}\) có 8 cách chọn
Có 2010 cách xếp chữ số 9
Ỏ 2008 vị trí còn lại, mỗi vị trí có 9 cách chọn
Vị trí cuối cùng có 1 cách chọn
Do đó có 8.2010.9 \({9^{2008}}\) số.
Vậy số các số tự nhiên thỏa mãn yêu cầu bài toán là:
\({10^{2010}} – \left( {{{8.9}^{2009}} + {9^{2009}} + {{8.2010.9}^{2008}}} \right) = {10^{2010}} – {16161.9^{2008}}\) số
Câu 7. Nhân ngày phụ nữ Việt Nam 20/10, các bạn nam lớp 10A đến cửa hàng hoa để mua hoa tặng các cô giáo dạy lớp mình. Cửa hàng hoa có bán ba loại hoa: hoa hồng, hoa cẩm chướng và hoa đồng tiền ( số hoa mỗi loại đều lớn hơn hoặc bằng 8 ). Nhóm 8 bạn nam vào cửa hàng và chọn 8 bông hoa. Hỏi các bạn nam có bao nhiêu cách chọn số lượng từng loại hoa?
A. 40320 .
B. 6720 .
C. 336 .
D. 45 .
Lời giải
Chọn D
Nhóm 8 bạn nam chọn ra 8 bông hoa gồm x hoa hồng, y hoa cẩm chướng và z hoa đồng tiền. Ta coi mỗi sự lựa chọn là một bộ ba số (x,y,z) sao cho x,y,z là các số nguyên không âm và thỏa mãn x+y+z=8. Mỗi bộ (x,y,z) như vậy ta đặt tương ứng với một dãy nhị phân độ dài 10 gồm 8 kí tự 1 và 2 kí tự 0 như sau:
\(\underbrace {11 \ldots 1}_x0\underbrace {11 \ldots 1}_y0\underbrace {11 \ldots 1}_z\)
Chẳng hạn bộ (3;1;4) ứng với sự lựa chọn 3 hoa hồng, 1 hoa cẩm chướng và 4 hoa đồng tiền được đặt tương ứng với dãy nhị phân 1110101111 .
Vì với mỗi dãy nhị phân độ dài 10 gồm 8 kí tự 1 và 2 kí tự 0 như trên tương ứng với cách chọn 2 vị trí trong 10 vị trí để ghi số 0,8 vị trí còn lại ghi số 1 nên số dãy nhị phân như trên là \(C_{10}^2 = 45\).
Vậy có 45 cách lựa chọn hoa thỏa yêu cầu bài toán.
Câu 8. Cho dãy số \(\left( {{u_n}} \right)\) được xác định như sau: Số hạng thứ n là số các số tự nhiên có n chữ số trong đó chỉ gồm các chữ số 1,2,3 và mỗi số có mặt ít nhất 1 lần. Tìm tổng của 9 số hạng đầu tiên.
A. 26844 .
B. 28464 .
C. 24684 .
D. 26484 .
Lời giải
Chọn D
Ta sẽ tìm số hạng tổng quát của \(\left( {{u_n}} \right)\)
Xét \({\rm{n}} = 1,{\rm{n}} = 2\) thì rõ ràng \({u_1} = {u_2} = 0\).
Bài toán phụ: Ta sẽ xác định xem có bao nhiêu số có n chữ số, trong đó các chữ số chỉ là 1,2,3 sao cho các chữ số xuất hiện trong đó là một hay hai trong ba chữ số đã cho
+ Số các số có n chữ số trong đó có mặt một trong ba chữ số {1,2,3 } là 3(11…1,22…2,33…3)
+ Trong ba số 1,2,3 có \(C_3^2\) tập gồm 2 chữ số.
Xét các số chỉ gồm hai số là 1,2
Mỗi chữ số có 2 cách chọn nên có \({2^n}\) số có n chữ số tạo thành từ {1;2}. Nên có \({2^n} – 2\) số có n chữ số được tạo thành từ {1;2} và mỗi chữ số có mặt ít nhất 1 lần ( trừ 11…1,22…2 )
Từ đó, số các số gồm n chữ số chỉ có mặt hai trong ba chữ số {1,2,3 } là \(C_3^2\left( {{2^n} – 2} \right)\).
Mặt khác có tất cả \({3^n}\) số các số tự nhiên có n chữ số được tạo thành từ các chữ số {1,2,3 } . Do đó có tất cả \({3^n} – C_3^2\left( {{2^n} – 2} \right) – 3 = {3^n} – {3.2^n} + 3\) số các số tự nhiên có n chữ số được tạo thành từ các chữ số {1,2,3 } và mỗi số có mặt ít nhất 1 lần.
Suy ra dãy số \(\left( {{u_n}} \right)\left\{ {\begin{array}{*{20}{c}}{{u_1} = {u_2} = 0}\\{{u_n} = {3^n} – {{3.2}^n} + 3(n \ge 3)}\end{array}} \right.\) hay \(\left( {{u_n}} \right) = {3^n} – {3.2^n} + 3\)
Vậy
\(\begin{array}{l}\sum\limits_{i = 1}^9 {{u_i}} = \sum\limits_{i = 1}^9 {\left( {{3^i} – {{3.2}^i} + 3} \right)} = \sum\limits_{i = 1}^9 {{3^i}} – 3\sum\limits_{i = 1}^9 {{2^i}} + 27\\ = \frac{{{3^{10}} – 3}}{{3 – 1}} – 3 \cdot \frac{{{2^{10}} – 2}}{{2 – 1}} + 27 = 26484\end{array}\).
Câu 9. Có bao nhiêu cách điền các số 1,2,3,4,5,6 (mỗi số một lần) vào các ô tròn ở trên Hình 1 sao cho tổng các số ở mỗi cạnh của tam giác là bằng nhau? (ví dụ ở hình 2 , tổng các số ở mỗi cạnh đều bằng 10).
Xem thêm