Giải SBT Toán lớp 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Giải trang 56 Tập 1
Bài 4.10 trang 56 Tập 1: Khi viết ∆ABC = ∆MNP thì góc nào tương ứng với góc PNM và cạnh nào tương ứng với cạnh NP. Hãy viết các cặp cạnh bằng nhau và các cặp góc bằng nhau của hai tam giác ABC và MNP đã cho.
Hướng dẫn giải
Khi viết ∆ABC = ∆MNP thì góc CBA tương ứng với góc PNM và cạnh BC tương ứng với cạnh NP.
Và ta có các cặp cạnh bằng nhau và các cặp góc bằng nhau là:
.
Bài 4.11 trang 56 Tập 1: Với hai tam giác ABC và MNP bất kì, sao cho ∆ABC = ∆MNP, những câu nào dưới đây đúng?
a) AB = MN, AC = MP, BC = NP.
b)
c) BA = NM, CA = PM, CB = PN.
d)
Hướng dẫn giải
Khi ∆ABC = ∆MNP ta có các cặp cạnh bằng nhau và các cặp góc bằng nhau là:
.
Từ đây ta rút ra được các khẳng định đúng là a, b, c.
Bài 4.12 trang 56 Tập 1: Với hai tam giác ABC và DEF bất kì, sao cho ∆ABC = ∆DEF, những câu nào dưới đây đúng?
a) ∆BCA = ∆FED.
b) ∆CAB = ∆EDF.
c) ∆BAC = ∆EDF.
d) ∆CBA = ∆FDE.
Hướng dẫn giải
Khi ∆ABC = ∆DEF , ta có các cặp đỉnh tương ứng là A và D; B và E; C và F.
Vậy chỉ có đáp án c là đúng.
Giải trang 57 Tập 1
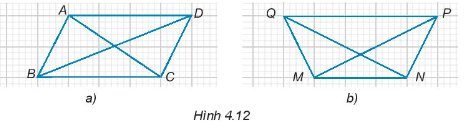
Bài 4.13 trang 57 Tập 1: Trong mỗi hình vẽ trên lưới ô vuông dưới đây, hãy chỉ ra một cặp hai tam giác bằng nhau.
Hướng dẫn giải
*) Ở Hình 4.12a) ta thấy: ∆ABC = ∆CDA vì:
AB = DC (đều bằng đường chéo hình chữ nhật được tạo thành từ hai ô vuông nhỏ)
AC: cạnh chung
BC = AD (bằng độ dài 4 ô vuông nhỏ xếp liền nhau)
Do đó, ∆ABC = ∆CDA (c – c – c).
*) Ở Hình 4.12b) ta thấy: ∆MQN = ∆NPM vì:
MQ = NP (đều bằng đường chéo hình chữ nhật được tạo thành từ hai ô vuông nhỏ)
MN: cạnh chung
PM = NQ (đều bằng độ dài đường chéo hình chữ nhật có chiều dài là 4 ô vuông xếp liền nhau và chiều rộng là hai ô vuông xếp liền nhau).
Do đó, ∆MQN = ∆NPM (c – c – c) .
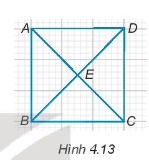
Bài 4.14 trang 57 Tập 1: Cho Hình 4.13, ABCD là hình vuông. E là giao của AC và BD. Hãy chỉ ra các cặp tam giác bằng nhau có chung đỉnh E.
Hướng dẫn giải
Ta có: AB = BC = CD = DA (đều bằng 3 ô vuông) và EA = EB = EC = ED.
Vậy theo trường hợp bằng nhau cạnh – cạnh – cạnh, ta có các cặp tam giác bằng nhau có chung đỉnh E là:
∆EAD = ∆EDC; ∆EAD = ∆ECB; ∆EAD = ∆EBA;
∆EDC = ∆ECB; ∆EDC = ∆EDA; ∆ECB = ∆EBA;
∆EAD = ∆ECD; ∆EAD = ∆EBC; ∆EAD = ∆EAB;
∆EDC = ∆EBC; ∆EDC = ∆EDA; ∆ECB = ∆EAB.
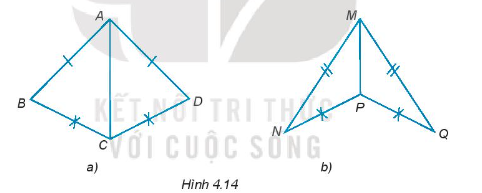
Bài 4.15 trang 57 Tập 1: Cho Hình 4.14, chứng minh rằng ∆ABC = ∆ADC; ∆MNP = ∆MQP.
Hướng dẫn giải
a) Xét ∆ABC và ∆ADC có:
AB = AD (giả thiết)
BC = DC (giả thiết)
AC chung
Do đó, ∆ABC = ∆ADC (c – c – c).
b) Xét ∆MNP và ∆MQP có:
MP chung
NP = PQ (giả thiết)
MN = MQ (giả thiết)
Do đó, ∆MNP = ∆MQP (c – c – c).
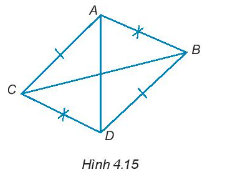
Bài 4.16 trang 57 Tập 1: Cho Hình 4.15, chứng minh rằng ∆ABC = ∆DCB; ∆ADB = ∆DAC.
Hướng dẫn giải
Xét ∆ABC và ∆DCB có:
AB = DC (giả thiết)
AC = BD (giải thiết)
BC chung
Do đó, ∆ABC = ∆DCB (c – c – c).
Xét hai tam giác ∆ADB và ∆DAC có:
AB = DC (giả thiết)
BD = AC (giải thiết)
AD chung
Do đó, ∆ADB = ∆DAC (c – c – c).
Bài 4.17 trang 58 Tập 1: Cho Hình 4.16, biết rằng , , hãy tính số đo các góc của tam giác ABC.
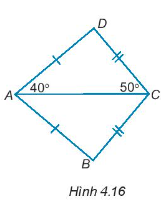
Hướng dẫn giải
Xét tam giác ADC có:
(định lí tổng ba góc trong tam giác)
40° + 50° + = 180°
= 180° – 40° – 50°
= 90°
Xét ∆ADC và ∆ABC có:
AD = AB (giả thiết)
DC = BC (giả thiết)
AC chung
Do đó, ∆ADC = ∆ABC (c – c – c)
Suy ra, ; ; (các góc tương ứng).
Do đó, = 40°; = 50°; = 90°.
Vậy tam giác ABC có = 40°; = 50°; = 90°.
Giải trang 58 Tập 1
Bài 4.18 trang 58 Tập 1: Cho Hình 4.17, biết rằng AD = BC, AC = BD và , hãy tính số đo của góc DEC.
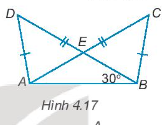
Hướng dẫn giải
Xét ∆ADB và ∆BCA có:
AD = BC (giả thiết)
BD = CA (giả thiết)
AB chung
Do đó, ∆ADB = ∆BCA (c – c – c).
Suy ra,
Mà = 30° nên = 30° hay .
Ta có: .
Xét tam giác AEB có:
+ + = 180° (định lí tổng ba góc trong tam giác)
30° + 30° + = 180°
= 180° – 30° – 30°
= 120o
Mà và đối đỉnh nên = 120°.
Vậy = 120°.
Bài 4.19 trang 58 Tập 1: Cho các điểm A, B, C, D, E như Hình 4.18, biết rằng AB = AC, AD = AE, BD = CE. Chứng minh rằng .
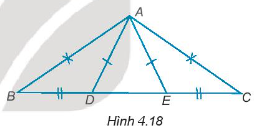
Hướng dẫn giải
Ta có:
BE = BD + DE
DC = CE + DE
Mà BD = CE nên BE = DC.
Xét hai tam giác ∆ABE và ∆ACD có:
AB = AC (giả thiết)
AE = AD (giả thiết)
BE = DC (chứng minh trên)
Do đó, ∆ABE = ∆ACD (c – c – c)
Suy ra, (hai góc tương ứng).
Bài 4.20 trang 58 Tập 1: Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau (H.4.19).
a) Chứng minh: ∆ABD = ∆DCA; ∆ADC = ∆BCD.
b) Bằng cách tính số đo góc ADC, hãy cho biết ABCD có phải hình chữ nhật không.
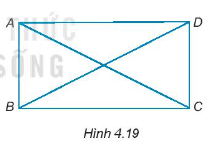
Hướng dẫn giải
a) Xét ∆ABD và ∆DCA có:
AB = CD (do ABCD là hình bình hành)
AD chung
BD = AC (giả thiết hai đường chéo bằng nhau)
Do đó, ∆ABD = ∆DCA (c – c – c).
Xét ∆ADC và ∆BCD có:
AD = BC (do ABCD là hình bình hành)
DC chung
AC = BD (giả thiết hai đường chéo bằng nhau)
Do đó, ∆ADC = ∆BCD (c – c – c).
b) Do ∆ABD = ∆DCA nên .
Mặt khác vì ABCD là hình bình hành nên AB // CD, do đó (hai góc trong cùng phía).
Do vậy .
Hình bình hành ABCD có một góc vuông nên ta suy ra các góc còn lại cũng là góc vuông. Vậy ABCD là hình chữ nhật.
Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 12: Tổng các góc trong một tam giác
Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Bài 15: Các trường hợp bằng nhau của tam giác vuông
Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
====== ****&**** =====