Giải SBT Toán 11 Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian
Bài 46 trang 116 SBT Toán 11: Cho hình hộp ABCD.A’B’C’D’.
a) Hình chiếu song song của điểm B’ trên mặt phẳng (ABCD) theo phương chiếu A’D là:
A. Điểm D.
B. Điểm C.
C. Điểm B.
D. Điểm A.
b) Hình chiếu song song của đoạn thẳng A’B trên mặt phẳng (CDD’C’) theo phương chiếu BC là:
A. Đoạn thẳng D’C.
B. Đoạn thẳng A’D’.
C. Đoạn thẳng AB’.
D. Đoạn thẳng A’B.
Lời giải:
a) Đáp án đúng là: B
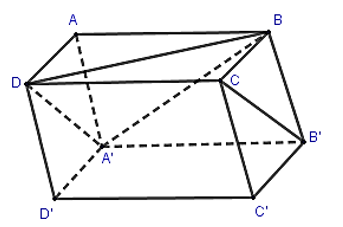
Vì ABCD và ABB’A’ là các hình bình hành nên ta suy ra được A’B’ // CD và A’B’ = CD (do cùng song song và bằng AB).
Suy ra A’B’CD là hình bình hành. Do đó, B’C // A’D.
Vậy hình chiếu song song của điểm B’ trên mặt phẳng (ABCD) theo phương chiếu A’D là điểm C.
b) Đáp án đúng là: A
Ta có hình chiếu song song của điểm B trên mặt phẳng (CDD’C’) theo phương chiếu BC là điểm C. (1)
Vì ABCD là hình bình hành nên BC // AD.
Vì ADD’A’ là hình bình hành nên A’D’ // AD.
Suy ra A’D’ // BC.
Do đó, hình chiếu song song của điểm A’ trên mặt phẳng (CDD’C’) theo phương chiếu BC là điểm D’. (2)
Từ (1) và (2) suy ra hình chiếu song song của đoạn thẳng A’B trên mặt phẳng (CDD’C’) theo phương chiếu BC là đoạn thẳng D’C.
Bài 47 trang 117 SBT Toán 11: Trong các Hình 44a, b, c, có bao nhiêu hình có thể là hình biểu diễn cho hình chóp tứ giác?
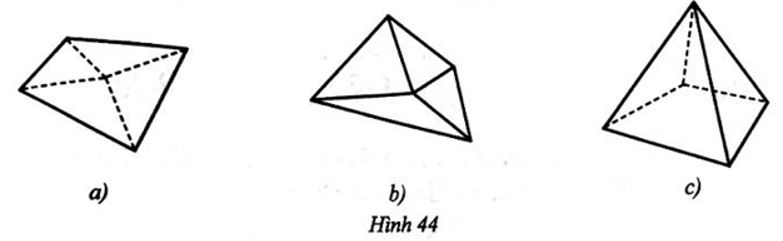
A. 3.
B. 2.
C. 1.
D. 0.
Lời giải:
Đáp án đúng là: A
Các hình đã cho đều có thể là hình biểu diễn cho hình chóp tứ giác.
Bài 48 trang 117 SBT Toán 11: Hình biểu diễn của hai đường thẳng cắt nhau có thể là hai đường thẳng song song được không? Vì sao?
Lời giải:
Giả sử hai đường thẳng a, b cắt nhau tại O và hình chiếu song song của a, b, O lần lượt là a’, b’, O’. Như vậy, O′ thuộc a’, O’ thuộc b’. Do đó a, b’ không thể song song vì có ít nhất một điểm chung O’.
Bài 49 trang 117 SBT Toán 11: Hình biểu diễn của hai đường thẳng chéo nhau có thể là hai đường thẳng song song được không? Vì sao?
Lời giải:
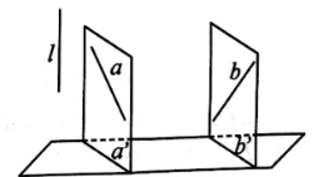
Giả sử a và b là hai đường thẳng chéo nhau có hình chiếu song song lần lượt là a’ và b’ lên một mặt phẳng.
Nếu mặt phẳng (a, a’) và mặt phẳng (b, b’) song song với nhau thì a’ // b’.
Vậy hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau.
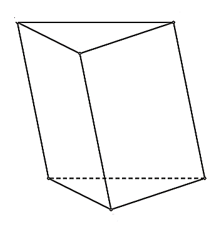
Bài 50 trang 117 SBT Toán 11: Vẽ hình biểu diễn của hình lăng trụ có đáy là tam giác đều.
Lời giải:
Vì tam giác bất kì có thể xem là hình biểu diễn của tam giác đều, do đó, hình biểu diễn của hình lăng trụ có đáy là tam giác đều có thể biểu diễn như hình vẽ dưới đây:
Bài 51* trang 117 SBT Toán 11: Cho tứ diện ABCD có M, N lần lượt là trung điểm của các cạnh AB, CD. Xác định ảnh của tứ diện ABCD qua phép chiếu song song có phương chiếu là đường thẳng MN, mặt phẳng chiếu là mặt phẳng (Q) bất kì cắt đường thẳng MN.
Lời giải:
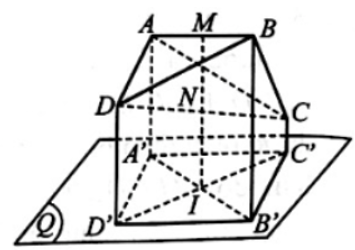
Gọi f là phép chiếu song song có phương chiếu là đường thẳng MN, mặt phẳng chiếu là mặt phẳng (Q) bất kì cắt đường thẳng MN.
Gọi A’, B’, C’, D’ là ảnh của A, B, C, D; I là ảnh của M, N qua phép chiếu f.
Vì M là trung điểm của AB nên I là trung điểm của A’B’; N là trung điểm của CD nên I là trung điểm của C’D’. Do đó tứ giác A’C’B’D’ là hình bình hành.
Vậy ảnh của tứ diện ABCD qua phép chiếu song song f là hình bình hành A’C’B’D’ cùng với hai đường chéo A’B’, C’D’ của nó.