Giải SBT Toán 11 Bài 1: Đường thẳng và mặt phằng trong không gian
Bài 1 trang 94 SBT Toán 11: Cho hình chóp tứ giác S.ABCD có ABCD là hình bình hành. Điểm M thuộc cạnh SC. Trong các mặt phẳng sau, điểm M nằm trên mặt phẳng nào?
A. (ABCD)
B. (SAC)
C. (SAB)
D. (SAD)
Lời giải:
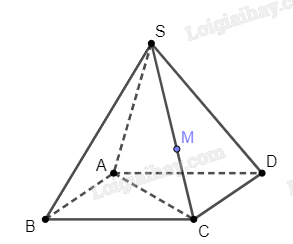
Theo hình vẽ, ta thấy SC nằm trong mặt (SAC).
Do nên M nằm trên mặt phẳng (SAC).
Đáp án đúng là B.
Bài 2 trang 94 SBT Toán 11: Cho hình tứ diện ABCD. Giao tuyến của hai mặt phẳng (ABC) và (CDA) là đường thẳng:
A. AB
B. BD
C. CD
D. AC
Lời giải:
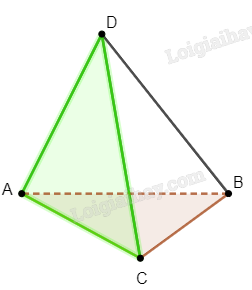
Xét hai mặt phẳng (ABC) và (CDA), ta nhận thấy hai mặt phẳng này có hai điểm chung là A và C, do đó giao tuyến của hai mặt phẳng này là AC.
Đáp án đúng là D.
Bài 3 trang 94 SBT Toán 11: Một đồ vật trang trí có bốn mặt phân biệt là các tam giác (xem hình dưới đây). Vẽ hình hiểu diễn của đồ vật đó.
Lời giải:
Do đồ vật trang trí có 4 mặt là các tam giác, nên nó có hình dạng một tứ diện.
Hình biểu diễn của nó như sau:
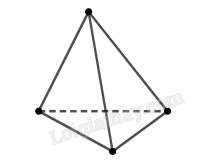
Bài 4 trang 94 SBT Toán 11: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng bốn điểm M, N, C, D không cùng nằm trong một mặt phẳng.
Lời giải:
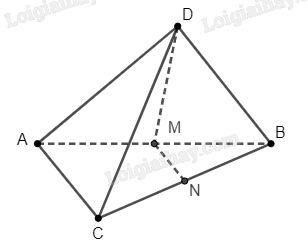
Do là trung điểm của , nên 4 điểm , , , cùng nằm trong mặt phẳng.
Giả sử 4 điểm , , , cùng nằm trong một mặt phẳng.
Điều này có nghĩa là .
Do bốn điểm , , , cùng nằm trong mặt phẳng, ta suy ra .
Điểm và điểm cùng nằm trong mặt phẳng , nên .
Mặt khác, do là trung điểm của , nên .
Suy ra . Điều này là vô lí do là tứ diện nên bốn điểm , , , không cùng nằm trong một mặt phẳng.
Bài 5 trang 95 SBT Toán 11: Cho hai mặt phẳng (P), (Q) cắt nhau theo giao tuyến d và hai đường thẳng a, b lần lượt nằm trong (P), (Q). Chứng minh rằng nếu hai đường thẳng a, b cắt nhau thì giao điểm của chúng thuộc đường thẳng d.
Lời giải:
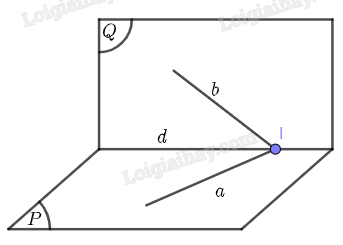
Gọi là giao điểm của hai đường thẳng và . Suy ra
Vì và , ta suy ra , tức là thuộc giao tuyến của hai mặt phẳng và . Mà , suy ra .
Bài toán được chứng minh.
Bài 6 trang 95 SBT Toán 11: Cho tứ diện . Trên các cạnh lần lượt lấy các điểm sao cho .
a) Xác định giao tuyến của mặt phẳng với các mặt phẳng , , .
b) Xác định giao điểm của đường thẳng với mặt phẳng .
c) Xác định giao tuyến của hai mặt phẳng và .
Lời giải:
a)
Giao tuyến của và :
Ta có .
Mặt khác, ta có .
Như vậy giao tuyển của và là đường thẳng .
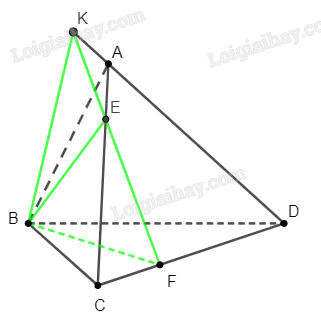
Giao tuyến của và :
Ta có .
Mặt khác, .
Như vậy giao tuyển của và là đường thẳng .
Giao tuyến của và :
Ta có
Mặt khác,
Như vậy giao tuyển của và là đường thẳng .
b) Trên mặt phẳng , lấy là giao điểm của và .
Ta có , mà .
Suy ra , tức là giao điểm của và .
c) Ta có .
Theo câu b, ta có
Mà nên ta suy ra .
Vậy giao tuyến của hai mặt phẳng và là đường thẳng .
Bài 7 trang 95 SBT Toán 11: Cho hình chóp có đáy là hình bình hành. Gọi lần lượt là trung điểm của các cạnh .
a) Xác định giao điểm của đường thẳng với mặt phẳng .
b) Xác định giao tuyến của mặt phẳng với các mặt phẳng .
Lời giải:
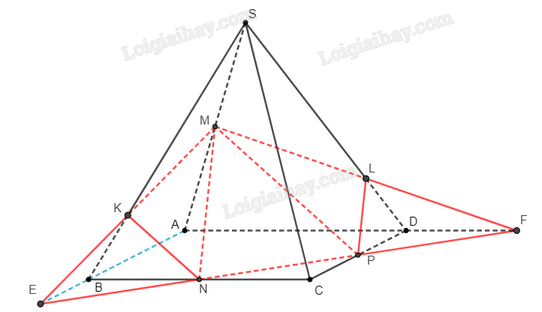
a) Xét mặt phẳng , gọi là giao điểm của và .
Ta có , mà nên .
b)
Giao tuyến của và :
Ta có .
Mặt khác, theo câu a, ta có .
Từ đó, giao tuyến của hai mặt phẳng và là đường thẳng .
Giao tuyến của và :
Trên mặt phẳng , gọi là giao điểm của và .
Vì là giao điểm của và , ta suy ra .
Do , nên ta có .
Hơn nữa, ta cũng có .
Vậy giao tuyến của hai mặt phẳng và là đường thẳng .
Giao tuyến của và :
Ta có là giao tuyến của hai mặt phẳng và .
Trên mặt phẳng , gọi .
Suy ra .
Hơn nữa, ta có .
Vậy giao tuyến của hai mặt phẳng và là đường thẳng .
Giao tuyến của và :
Ta có là giao tuyến của hai mặt phẳng và .
Trên mặt phẳng , gọi .
Suy ra .
Hơn nữa, ta có .
Vậy giao tuyến của hai mặt phẳng và là đường thẳng .
Bài 8 trang 95 SBT Toán 11: Cho hình chóp có đáy là hình bình hành. Gọi lần lượt là trung điểm của các cạnh .
a) Xác định giao điểm của đường thẳng với mặt phẳng .
b) Xác định giao điểm của đường thẳng với mặt phẳng .
Lời giải:
a) Trên mặt phẳng , gọi .
Trên mặt phẳng , gọi .
Do , ta suy ra .
Vậy là giao điểm của và .
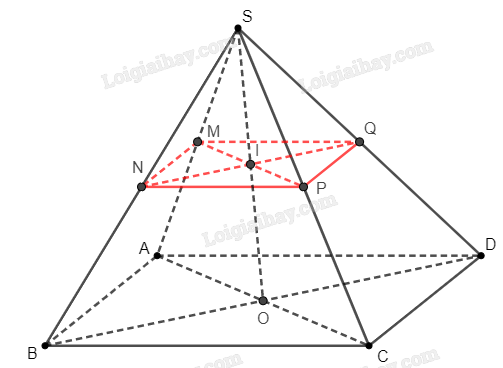
b) Trên mặt phẳng , gọi .
Do , ta suy ra .
Vậy là giao điểm của và .
Bài 9 trang 95 SBT Toán 11: Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi O là giao điểm của AC và BD. Trên SO lấy điểm I sao cho SI = 2IO.
a) Xác định các giao điểm M, N lần lượt của SA, SD với mặt phẳng (IBC).
b*) Chứng minh rằng các đường thẳng AD, BC và MN đồng quy.
Lời giải:
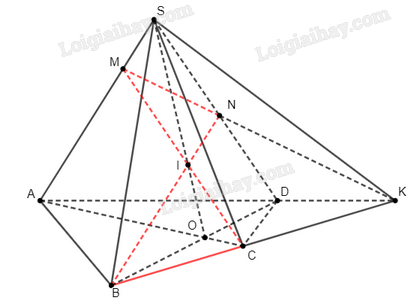
a)
Giao điểm của và :
Ta nhận xét rằng .
Trên mặt phẳng , gọi .
Do , nên .
Vậy là giao điểm của và .
Giao điểm của và :
Ta nhận xét rằng .
Trên mặt phẳng , gọi .
Do , nên .
Vậy là giao điểm của và .
b) Trên mặt phẳng , gọi là giao điểm của và .
Ta có .
Mặt khác, .
Vậy giao tuyến của và là đường thẳng .
Do , , , ta suy ra nằm trên giao tuyến của và , tức là .
Vậy ba đường thẳng , , cắt nhau tại .