Giải SBT Toán lớp 6 Bài 9: Dấu hiệu chia hết cho 3, cho 9
Bài 77 trang 27 sách bài tập Toán lớp 6 Tập 1: Cho các số 27; 45; 881; 916; 2 100; 2 439; 13 118; 35 550; 5 223 411. Trong các số đó:
a) Số nào chia hết cho 3?
b) Số nào lớn hơn 2 000 không chia hết cho 3?
c) Số nào chia hết cho 9?
d) Số nào nhỏ hơn 3 000 không chia hết cho 9?
Lời giải:
a) Ta có: 2 + 7 = 9 chia hết cho 3 nên 27 chia hết cho 3;
Ta có: 4 + 5 = 9 chia hết cho 3 nên 45 chia hết cho 3;
Ta có: 8 + 8 + 1 = 17 không chia hết cho 3 nên 881 không chia hết cho 3;
Ta có: 9 + 1 + 6 = 16 không chia hết cho 3 nên 916 không chia hết cho 3;
Ta có: 2 + 1 + 0 + 0 = 3 chia hết cho 3 nên 2 100 chia hết cho 3;
Ta có: 2 + 4 + 3 + 9 = 18 chia hết cho 3 nên 2 439 chia hết cho 3;
Ta có: 1 + 3 + 1 + 1 + 8 = 14 không chia hết cho 3 nên 13 118 không chia hết cho 3;
Ta có: 3 + 5 + 5 + 5 + 0 = 18 chia hết cho 3 nên 35 550 chia hết cho 3;
Ta có: 5 + 2 + 2 + 3 + 4 + 1 + 1 = 18 chia hết cho 3 nên 5 223 411 chia hết cho 3;
Vậy các số chia hết cho 3 là: 27; 45; 2 100; 2 439; 35 550; 5 223 411.
b) Các số còn lại là các số không chia hết cho 3 là: 881; 916; 13 118.
Trong các số này số lớn hơn 2 000 và không chia hết cho 3 là: 13 118.
Vậy số lớn hơn 2 000 và không chia hết cho 3 là: 13 118.
c) Ta có: 2 + 7 = 9 chia hết cho 9 nên 27 chia hết cho 9;
Ta có: 4 + 5 = 9 chia hết cho 9 nên 45 chia hết cho 9;
Ta có: 8 + 8 + 1 = 17 không chia hết cho 9 nên 881 không chia hết cho 9;
Ta có: 9 + 1 + 6 = 16 không chia hết cho 9 nên 916 không chia hết cho 9;
Ta có: 2 + 1 + 0 + 0 = 3 không chia hết cho 9 nên 2 100 không chia hết cho 9;
Ta có: 2 + 4 + 3 + 9 = 18 chia hết cho 9 nên 2 439 chia hết cho 9;
Ta có: 1 + 3 + 1 + 1 + 8 = 14 không chia hết cho 9 nên 13 118 không chia hết cho 9;
Ta có: 3 + 5 + 5 + 5 + 0 = 18 chia hết cho 9 nên 35 550 chia hết cho 9;
Ta có: 5 + 2 + 2 + 3 + 4 + 1 + 1 = 18 chia hết cho 9 nên 5 223 411 chia hết cho 9;
Vậy các số chia hết cho 9 là: 27; 45; 2 439; 35 550; 5 223 411.
d) Các số không chia hết cho 9 mà nhỏ hơn 3 000 là: 881; 916; 2 100.
Bài 78 trang 27 sách bài tập Toán lớp 6 Tập 1: Tìm chữ số x để số 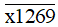 thỏa mãn mỗi điều kiện sau:
thỏa mãn mỗi điều kiện sau:
a) Chia hết cho 3;
b) Chia hết cho 9;
c) Chia hết cho 3, nhưng không chia hết cho 9.
Lời giải:
Ta có x + 1 + 2 + 6 + 9 = x + 18.
a) Để số đã cho chia hết cho 3 thì x + 18 chia hết cho 3.
Khi đó x ∈ {0;3;6;9;12…}.
Mà x là chữ số và x khác 0 nên x ∈ {3;6;9}.
Vậy x ∈ {3;6;9}.
b) Để số đã cho chia hết cho 9 thì x + 18 chia hết cho 9.
Khi đó x ∈ {0;9;18;…}.
Mà x là chữ số và x khác 0 nên x = 9.
Vậy x = 9.
c) Để số đã cho chia hết cho 3, nhưng không chia hết cho 9 thì x + 18 chia hết cho 3, nhưng không chia hết cho 9.
Khi đó x ∈ {3;6;12;15…}.
Mà x là chữ số nên x ∈ {3;6}.
Vậy x ∈ {3;6}.
Bài 79 trang 27 sách bài tập Toán lớp 6 Tập 1: Có bao nhiêu số có dạng 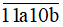 chia cho 5 dư 1 và chia hết cho 9?
chia cho 5 dư 1 và chia hết cho 9?
Lời giải:
Để số 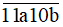 chia cho 5 dư 1 thì b ∈ {1;6}.
chia cho 5 dư 1 thì b ∈ {1;6}.
TH1: b = 1
Ta có: 1 + 1 + a + 1 + 0 + 1 = a + 4
Để số 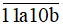 chia hết cho 9 thì a + 4 chia hết cho 9 mà a là chữ số nên a = 5.
chia hết cho 9 thì a + 4 chia hết cho 9 mà a là chữ số nên a = 5.
Suy ra 115 101 thỏa mãn chia 5 dư 1 và chia hết cho 9.
TH2: b = 6
Ta có: 1 + 1 + a + 1 + 0 + 6 = a + 9
Để số 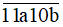 chia hết cho 9 thì a + 9 chia hết cho 9 mà a là chữ số nên a = 0 hoặc a = 9.
chia hết cho 9 thì a + 9 chia hết cho 9 mà a là chữ số nên a = 0 hoặc a = 9.
Suy ra 110 106 và 119 106 thỏa mãn chia cho 5 dư 1 và chia hết cho 9.
Vậy có ba số chia hết cho 9, chia 5 dư 1.
Bài 80 trang 27 sách bài tập Toán lớp 6 Tập 1: Không tính giá trị biểu thức, hãy giải thích tại sao mỗi biểu thức sau chia hết cho 3:
a) A = 1 233 + 42 312 + 72 036;
b) B = 111 + 222 + 333 + … + 999.
Lời giải:
a) Ta có: 1 + 2 + 3 + 3 = 9 chia hết cho 3 nên 1 223 chia hết cho 3;
Ta có: 4 + 2 + 3 + 1 + 2 = 12 chia hết cho 3 nên 42 312 chia hết cho 3;
Ta có: 7 + 2 + 0 + 3 + 6 = 18 chia hết cho 3 nên 72 036 chia hết cho 3;
Do đó: 1 233 + 42 312 + 72 036 chia hết cho 3.
Vậy A = 1 233 + 42 312 + 72 036 chia hết cho 3.
b) B = 111 + 222 + 333 + … + 999
= 111 + 2.111 + 3.111 + … + 9.111
= 111.(1 + 2 + 3 + … + 9)
Ta có: 1 + 1 + 1 = 3 chia hết cho 3 nên 111 chia hết cho 3.
Do đó 111.(1 + 2 + 3 + … + 9) chia hết cho 3.
Vậy B = 111 + 222 + 333 + … + 999 chia hết cho 3.
Bài 81 trang 27 sách bài tập Toán lớp 6 Tập 1: Không tính giá trị biểu thức, hãy giải thích tại sao mỗi biểu thức sau chia hết cho 9:
a) P = 81 + 108 + 918;
b) M = 12.585 + 13.63 333 + 14. 378 225 + 18.5 142 312;
c) N = 11 + 22 + 33 + … + 99 + 2 021.60 021.
Lời giải:
a) Ta có: 8 + 1 = 9 chia hết cho 9 nên 81 chia hết cho 9;
Ta có: 1 + 0 + 8 = 9 chia hết cho 9 nên 108 chia hết cho 9;
Ta có: 9 + 1 + 8 = 18 chia hết cho 9 nên 918 chia hết cho 9;
Do đó: 81 + 108 + 918 chia hết cho 9.
Vậy P = 81 + 108 + 918 chia hết cho 9.
b) Ta có: 5 + 8 + 5 =18 chia hết cho 9 nên 585 chia hết cho 9. Do đó 12.585 chia hết cho 9.
Ta có: 6 + 3 + 3 + 3 + 3 = 18 chia hết cho 9 nên 63 333 chia hết cho 9. Do đó 13.63 333 chia hết cho 9.
Ta có: 3 + 7 + 8 + 2 + 2 + 5 = 27 chia hết cho 9 nên 378 225 chia hết cho 9. Do đó 14. 378 225 chia hết cho 9
Ta có: 5 + 1 + 4 + 2 + 3 + 1 + 2 = 18 chia hết cho 9 nên 5 142 312 chia hết cho 9. Do đó 18.5 142 312 chia hết cho 9.
Vậy M = 12.585 + 13.63 333 + 14. 378 225 + 18.5 142 312 chia hết cho 9.
c) N = 11 + 22 + 33 + … + 99 + 2 021.60 021
= (11 + 88) + (22 + 77) + (33 + 66) + (44 + 55) + 99 + 2 021.60 021
= 99 + 99 + 99 + 99 + 99 + 2 021.60 021.
Ta có: 9 + 9 = 18 chia hết cho 9 nên 99 chia hết cho 9;
6 + 0 + 0 + 2 + 1 = 9 chia hết cho 9 nên 60 021 chia hết cho 9. Do đó 2 021.60 021 chia hết cho 9.
Suy ra 99 + 99 + 99 + 99 + 99 + 2 021.60 021 chia hết cho 9.
Vậy N = 11 + 22 + 33 + … + 99 + 2 021.60 021 chia hết cho 9.
Bài 82 trang 27 sách bài tập Toán lớp 6 Tập 1: Tìm các số tự nhiên a, b sao cho:
a) 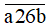 chia hết cho cả 2, 3, 5 và 9;
chia hết cho cả 2, 3, 5 và 9;
b) 123.a + 9 873.b = 2 227 691.
Lời giải:
a) Để số chia hết cho 2, 5 thì b = 0;
Khi đó số cần tìm là: 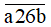
Ta có: a + 2 + 6 + 0 = a + 8;
Để số 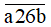 chia hết cho 3 và 9 thì a + 8 chia hết cho 3 và 9.
chia hết cho 3 và 9 thì a + 8 chia hết cho 3 và 9.
Mà a là chữ số và a khác 0 nên a = 1.
Vậy a = 1, b = 0 thì số 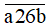 chia hết cho cả 2, 3, 5 và 9.
chia hết cho cả 2, 3, 5 và 9.
b) Ta có 1 + 2 + 3 = 6 chia hết cho 3 nên 123 chia hết cho 3. Do đó 123.a chia hết cho 3.
Ta có: 9 + 8 + 7 + 3 = 27 chia hết cho 3 nên 9 873 chia hết cho 3. Do đó 9 873.b chia hết cho 3.
Vì vậy 123.a + 9 873.b chia hết cho 3.
Ta lại có: 2 + 2 + 2 + 7 + 6 + 9 + 1 = 29 không chia hết cho 3.
Do đó không tồn tại a và b thỏa mãn yêu cầu bài toán.
Bài 83 trang 27 sách bài tập Toán lớp 6 Tập 1:
a) Có bao nhiêu số tự nhiên có hai chữ số chia cho 3 dư 1?
b) Có bao nhiêu số tự nhiên có ba chữ số chia cho 9 dư 2?
c) Có bao nhiêu số tự nhiên có hai chữ số 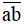 sao cho
sao cho 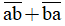 chia hết cho 9?
chia hết cho 9?
Lời giải:
a) Các số tự nhiên có hai chữ số chia cho 3 dư 1 là: 10; 13; …; 97.
Số các số tự nhiên có hai chữ số chia cho 3 dư 1 là: (97 – 10):3 + 1 = 30 số.
Vậy có 30 số tự nhiên có hai chữ số chia cho 3 dư 1.
b) Các số tự nhiên có ba chữ số chia cho 9 dư 2 là: 101; 110; 119; 128; 237; …; 992.
Số các số tự nhiên có ba chữ số chia cho 9 dư 2 là: (992 – 101): 9 + 1 = 100.
Vậy có 100 số tự nhiên có ba chữ số chia cho 9 dư 2.
c) Ta có: 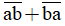 = 10a + b + 10b + a = 11a + 11b = 11.(a + b)
= 10a + b + 10b + a = 11a + 11b = 11.(a + b)
Vì 11 không chia hết cho 9 nên a + b chia hết cho 9.
Mà a, b là các chữ số nên a, b ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}
Các cặp số (a; b) là: (1; 8), (8; 1), (7; 2), (2; 7), (6; 3) (3; 6), (4; 5), (5; 4), (9; 9), (9; 0) thỏa mãn tổng chia hết cho 9.
Do đó 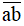 ∈ {18;81,72;27;63;36;45;54;99;90}.
∈ {18;81,72;27;63;36;45;54;99;90}.
Vậy có tất cả 10 số tự nhiên 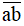 thỏa mãn bài toán.
thỏa mãn bài toán.
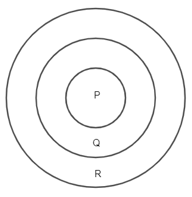
Bài 84 trang 28 sách bài tập Toán lớp 6 Tập 1: Bạn Minh có chơi trò phi tiêu với ba cái tiêu. Lần thứ nhất, bạn Minh phi 2 tiêu vào vùng Q và 1 tiêu vào vùng R thì được 12 điểm. Lần thứ hai, bạn Minh phi 2 tiêu vào vùng P và 1 tiêu vào cùng R thì được 18 điểm. Lần thứ ba, bạn Minh phi trúng mỗi vùng một tiêu. Hỏi số điểm lần thứ ba của bạn Minh có chia hết cho cả 3 và 5 không? Tại sao?
Lời giải:
Tổng số điểm của bạn Minh ở hai lần đầu là: 12 + 18 (điểm).
Vì bạn Minh đã phi 2 tiêu vào vùng Q và 1 tiêu vào vùng R và phi 2 tiêu vào vùng P và 1 tiêu vào cùng R.
Như vậy sau lần thứ nhất và lần thứ hai bạn Minh phi được 2 tiêu vào vùng Q, 2 tiêu R và 2 tiêu vào vùng P.
Suy ra tổng số điểm ba vùng là: 30:2 = 15 (điểm).
Do lần thứ ba, bạn Minh phi trúng mỗi vùng một tiêu nên số điểm lần thứ ba là 15 điểm.
Ta thấy 15 có chữ số tận cùng là 5 nên chia hết cho 5, 1 + 5 = 6 chia hết cho 3 nên 15 chia hết cho 3.
Vậy số điểm lần thứ ba của bạn Minh chia hết cho cả 3 và 5.
Bài 85 trang 28 sách bài tập Toán lớp 6 Tập 1: Cho a là số tự nhiên có 2 004 chữ số và chia hết cho 9. Gọi b là tổng các chữ số của a; c là tổng các chữ số của b và d là tổng các chữ số của c. Tính d.
Lời giải:
Do a chia hết cho 9 nên tổng các chữ số của a chia hết cho 9. Mặt khác b là tổng các chữ số của a nên b chia hết cho 9.
Do b chia hết cho 9 nên tổng các chữ số của b chia hết cho 9. Mặt khác c là tổng các chữ số của b nên c chia hết cho 9.
Do c chia hết cho 9 nên tổng các chữ số của c chia hết cho 9. Mặt khác d là tổng các chữ số của c nên d chia hết cho 9.
Vì a là số tự nhiên có 2 004 chữ số, mỗi chữ số của a đều không vượt quá 9 nên b ≤ 2 004.9 = 18 036. Nghĩa là b có 5 chữ số.
Suy ra c < 9 + 9 + 9 + 9 = 9.5 = 45. Mặt khác c ≠ 0 và c chia hết cho 9 nên suy ra c ∈ {9; 18; 27; 36}.
Ta có d là tổng các chữ số của c nên d = 9 = 1 + 8 = 2 + 7 = 3 + 6.
Vậy d = 9.
Bài 86 trang 28 sách bài tập Toán lớp 6 Tập 1: Viết liên tiếp các số tự nhiên từ 10 đến 99 liền nhau ta được một số tự nhiên. Hỏi số đó chia hết cho 9 hay không? Vì sao?
Lời giải:
Gọi A là số được viết bởi 90 số từ 10 đến 99.
Tổng các chữ số hàng đơn vị của số này là: (0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9). 9 = 405.
Tổng các chữ số hàng chục của số này là: (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9).10 = 450.
Vậy tổng các chữ số của số A là: 405 + 450 = 855.
Vì 8 + 5 + 5 =18 chia hết cho 9 nên 855 chia hết cho 9.
Vậy số A chia hết cho 9.
Bài 87 trang 28 sách bài tập Toán lớp 6 Tập 1: Không thực hiện phép tính, hãy giải thích tại sao phép nhân là sai: 7 654.658 = 5 136 332.
Lời giải:
Ta có: 7 + 6 + 5 + 4 = 22 chia cho 9 dư 4 nên 7 654 chia cho 9 dư 4.
Ta lại có: 6 + 5 + 8 = 19 chia cho 9 dư 1 nên 658 chia cho 9 dư 1.
Do đó 7 654.658 chia 9 dư 4.
Ta có: 5 + 1 + 3 + 6 + 3 + 3 + 2 = 23 chia cho 9 dư 3 nên 5 136 332 chia cho 9 dư 3.
Vậy phép tính 7 654.658 = 5 136 332 là sai.
Bài 88 trang 28 sách bài tập Toán lớp 6 Tập 1: Một công ty có 9 contenơ hàng với khối lượng hàng mỗi contenơ là: 193 tạ, 239 tạ, 277 tạ, 297 tạ, 316 tạ, 321 tạ, 329 tạ, 346 tạ, 355 tạ. Trong sáu tháng đầu năm công ty đó đã xuất khẩu 8 contenơ hàng, trong đó lượng hàng xuất khẩu của Quý II gấp 8 lần Quý I. Contenơ hàng còn lại có khối lượng bằng bao nhiêu?
Lời giải:
Tổng khối lượng hàng của 9 contenơ hàng là:
193 + 239 + 277 + 297 + 316 + 321 + 329 + 346 + 355 = 2 673 (tạ).
Ta có: 2 + 6 + 7 + 3 = 18 chia hết cho 9 nên 2 673 chia hết cho 9.
Vì lượng hàng xuất khẩu của Quý II gấp 8 lần Quý I nên số lượng hàng trong 6 tháng đầu năm phải chia hết cho 9.
Do đó khối lượng hàng của contenơ còn lại phải chia hết cho 9.
Trong số 9 contenơ trên chỉ có contenơ có khối lượng 297 tạ là thỏa mãn chia hết cho 9.
Vậy contenơ hàng còn lại có khối lượng là 297 tạ.
====== ****&**** =====