Lý thuyết Toán lớp 6 Bài 8: Dấu hiệu chia hết cho 2, cho 5
Video giải Toán 6 Bài 8: Dấu hiệu chia hết cho 2, cho 5 – Cánh diều
A. Lý thuyết Dấu hiệu chia hết cho 2, cho 5
I. Dấu hiệu chia hết cho 2
Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
Ví dụ:
+ Các số 234, 356,… lần lượt có chữ số tận cùng là 4 và 6 nên chúng chia hết cho 2.
+ Các số 1 230, 2 548,… lần lượt có chữ số tận cùng là 0 và 8 nên chúng chia hết cho 2.
II. Dấu hiệu chia hết cho 5
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Ví dụ:
+ Các số 120, 355,… lần lượt có chữ số tận cùng là 0 và 5 nên chúng chia hết cho 5.
+ Các số 1 120, 5 345,… lần lượt có chữ số tận cùng là 0 và 5 nên chúng chia hết cho 5.
Nhận xét: Từ dấu hiệu chia hết cho 2 và 5 ở trên, ta thấy những số chia hết cho cả 2 và 5 là những số có chữ số tận cùng là 0.
Ví dụ: Các số 100, 1 290, … đều chia hết cho cả 2 và 5 và chúng đều có chữ số tận cùng là 0.
B. Bài tập tự luyện
Bài 1. Cho các số 82, 980, 5 975, 49 173, 756 598. Trong các số đó:
a) Số nào chia hết cho 5, nhưng không chia hết cho 2?
b) Số nào chia hết cho 2, nhưng không chia hết cho 5?
c) Số nào không chia hết cho 2 và không chia hết cho 5?
Lời giải:
a) Số chia hết cho 5 nhưng không chia hết cho 2 có chữ số tận cùng là 5.
Nên trong các số đã cho, số chia hết cho 5 nhưng không chia hết cho 2 là: 5 975.
b) Số chia hết cho 2 nhưng không chia hết cho 5 có chữ số tận cùng là 2; 4; 6; 8.
Nên trong các số đã cho, các số chia hết cho 2 nhưng không chia hết cho 5 là: 82; 756 598.
c) Số không chia hết cho 2 và không chia hết cho 5 thì không có tận cùng là 0; 2; 4; 5; 6; 8, hay nói cách khác là các số có chữ số tận cùng là 1; 3; 7; 9 thì không chia hết cho cả 2 và 5.
Do đó, trong các số đã cho số không chia hết cho 2 và không chia hết cho 5 là: 49 173.
Bài 2. Cho số N =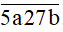 
Có bao nhiêu số N sao cho N là số có 5 chữ số khác nhau và N chia cho 5 dư 1 và N chia hết cho 2.
Lời giải:
Điều kiện: a, b ∈ {0; 1; 2; 3; ….; 9}
N =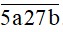 
chia cho 5 dư 1 nên b ∈ {1; 6}
Mà N chia hết cho 2 nên b = 6, ta được số N =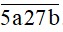 
Lại có N là số có 5 chữ số khác nhau nên a ∈ {0; 1; 3; 4; 8; 9}
Vậy có 6 số N thỏa mãn yêu cầu bài là 50 276; 51 276; 53 276; 54 276; 58 276; 59 276.
Xem thêm các bài tóm tắt lý thuyết Toán 6 Cánh diều hay, chi tiết khác:
Bài 7: Quan hệ chia hết. Tính chất chia hết
Bài 9: Dấu hiệu chia hết cho 3, cho 9
Bài 10: Số nguyên tố. Hợp số
Bài 11: Phân tích một số ra thừa số nguyên tố
Bài 12: Ước chung và ước chung lớn nhất
====== ****&**** =====