Tìm khoảng đồng biến, nghịch biến của các hàm số sau: \(f\left( x \right) = \frac{1}{{ – x – 5}}\);

Câu hỏi:

Tìm khoảng đồng biến, nghịch biến của các hàm số sau:
\(f\left( x \right) = \frac{1}{{ – x – 5}}\);

Trả lời:

Hướng dẫn giải
Tập xác định của hàm số là: D = ℝ \ {– 5}.
+ Xét khoảng (– ∞; – 5):
Lấy hai số x₁, x₂ tùy ý thuộc (– ∞; – 5) sao cho x₁ < x₂.
Ta có: \(f\left( {{x_1}} \right) – f\left( {{x_2}} \right) = \frac{1}{{ – {x_1} – 5}} – \frac{1}{{ – {x_2} – 5}}\)\( = \frac{{ – {x_2} – 5 – \left( { – {x_1} – 5} \right)}}{{\left( { – {x_1} – 5} \right)\left( { – {x_2} – 5} \right)}}\)\( = \frac{{{x_1} – {x_2}}}{{\left( {{x_1} + 5} \right)\left( {{x_2} + 5} \right)}}\).
Vì x₁, x₂ ∈ (– ∞; – 5) nên x₁ + 5 < 0 và x₂ + 5 < 0.
Lại có: x₁ < x₂ nên x₁ – x₂ < 0.
Do đó, f(x₁) – f(x₂) \( = \frac{{{x_1} – {x_2}}}{{\left( {{x_1} + 5} \right)\left( {{x_2} + 5} \right)}}\) < 0 hay f(x₁) < f(x₂).
Vậy hàm số đồng biến trên khoảng (– ∞; – 5). (1)
+ Xét khoảng (– 5; + ∞):
Lấy hai số x₃, x₄ tùy ý thuộc (– 5; + ∞) sao cho x₃ < x₄.
Ta có: \(f\left( {{x_3}} \right) – f\left( {{x_4}} \right) = \frac{1}{{ – {x_3} – 5}} – \frac{1}{{ – {x_4} – 5}}\)\( = \frac{{ – {x_4} – 5 – \left( { – {x_3} – 5} \right)}}{{\left( { – {x_3} – 5} \right)\left( { – {x_4} – 5} \right)}}\)\( = \frac{{{x_3} – {x_4}}}{{\left( {{x_3} + 5} \right)\left( {{x_4} + 5} \right)}}\).
Vì x₃, x₄ ∈ (– 5; + ∞) nên x₃ + 5 > 0 và x₄ + 5 > 0.
Lại có: x₃ < x₄ nên x₃ – x₄ < 0.
Do đó, f(x₃) – f(x₄) \( = \frac{{{x_3} – {x_4}}}{{\left( {{x_3} + 5} \right)\left( {{x_4} + 5} \right)}}\) < 0 hay f(x₁) < f(x₂).
Vậy hàm số đồng biến trên khoảng (– 5; + ∞). (2)
Từ (1) và (2) suy ra hàm số đã cho đồng biến trên các khoảng (– ∞; – 5) và (– 5; + ∞).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tập xác định của các hàm số sau: f(x) = \(\frac{{4x – 1}}{{\sqrt {2x – 5} }}\);
   
   

   Câu hỏi:
   

   Tập xác định của các hàm số sau:
   f(x) = \(\frac{{4x – 1}}{{\sqrt {2x – 5} }}\);

   Trả lời:

   Hướng dẫn giải
   Biểu thức \(\frac{{4x – 1}}{{\sqrt {2x – 5} }}\) có nghĩa khi 2x – 5 > 0 hay x > \(\frac{5}{2}\).
   Vậy tập xác định của hàm số là D = \(\left( {\frac{5}{2};\,\, + \infty } \right)\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. f(x) = \(\frac{{2 – x}}{{\left( {x + 3} \right)\left( {x – 7} \right)}}\);
   
   

   Câu hỏi:
   

   f(x) = \(\frac{{2 – x}}{{\left( {x + 3} \right)\left( {x – 7} \right)}}\);

   Trả lời:

   Hướng dẫn giải

   Biểu thức \(\frac{{2 – x}}{{\left( {x + 3} \right)\left( {x – 7} \right)}}\) có nghĩa khi (x + 3)(x – 7) ≠ 0 ⇒ x ≠ – 3 và x ≠ 7.
   Vậy tập xác định của hàm số là D = ℝ \ {– 3; 7}.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. f⁢(x)={1x-3   ⁢k⁢h⁢i⁢x≥0⁢ 1   k⁢h⁢i⁢x
   
   

   Câu hỏi:
   

   $f\left(x\right)=\{\begin{array}{c}\frac{1}{x–3} khix\ge 0\hspace{1em}\\ 1 \hspace{1em}\hspace{0.5em}khix<0\end{array}.$

   Trả lời:

   Hướng dẫn giải
   Hàm số lấy giá trị bằng 1 khi x < 0 nên hàm số xác định với mọi x < 0.
   Khi x ≥ 0, hàm số xác định khi và chỉ khi x – 3 ≠ 0 ⇒ x ≠ 3.
   Vậy tập xác định của hàm số là D = ℝ \ {3}.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Vẽ đồ thị các hàm số sau: \(f\left( x \right) = \left\{ \begin{array}{l}{x^2}\,\,\,\,\,\,\,\,\,khi\,\,x \le 2\\x + 2\,\,\,khi\,\,x > 2;\end{array} \right.\)
   
   

   Câu hỏi:
   

   Vẽ đồ thị các hàm số sau:
   \(f\left( x \right) = \left\{ \begin{array}{l}{x^2}\,\,\,\,\,\,\,\,\,khi\,\,x \le 2\\x + 2\,\,\,khi\,\,x > 2;\end{array} \right.\)

   Trả lời:

   Hướng dẫn giải
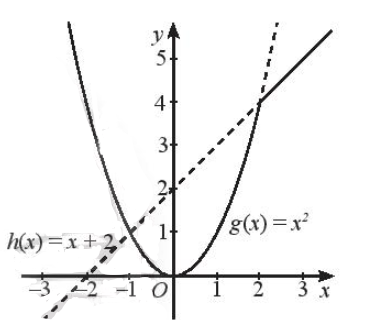
   + Vẽ đồ thị hàm số g(x) = x² và giữ lại phần đồ thị ứng với x ≤ 2:
   Đồ thị hàm số g(x) = x² là một parabol có đỉnh là gốc tọa độ O, trục đối xứng là trục Oy, đồ thị có bề lõm hướng lên trên, đi qua các điểm (1; 1), (– 1; 1), (2; 4), (– 2; 4).
   Ta giữ lại phần đồ thị nằm bên trái đường thẳng x = 2:
   + Vẽ đồ thị hàm số h(x) = x + 2 và giữ lại phần đồ thị ứng với x > 2.
   Đồ thị hàm số h(x) = x + 2 là một đường thẳng đi qua hai điểm (0; 2) và (– 2; 0).
   Ta giữ lại phần đường thẳng nằm bên phải đường thẳng x = 2.
   Ta được đồ thị cần vẽ như hình sau:
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. f(x) = |x + 3| – 2.
   
   

   Câu hỏi:
   

   f(x) = |x + 3| – 2.

   Trả lời:

   Hướng dẫn giải
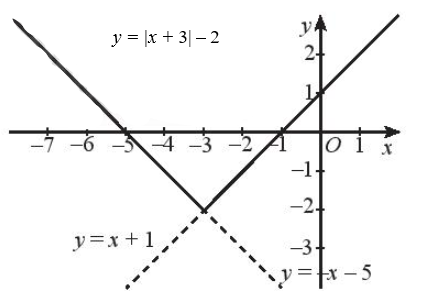
   Với x + 3 ≥ 0 ⇔ x ≥ – 3, ta có: |x + 3| – 2 = x + 3 – 2 = x + 1.
   Với x + 3 < 0 ⇔ x < – 3, ta có: |x + 3| – 2 = – (x + 3) – 2 = – x – 3 – 2 = – x – 5.
   Khi đó ta có: \(f\left( x \right) = \left\{ \begin{array}{l}x + 1\,\,\,\,\,\,\,khi\,\,x \ge – 3\\ – x – 5\,\,\,\,khi\,\,x < – 3\end{array} \right.\).
   Ta vẽ đồ thị hàm số g(x) = x + 1 và giữ lại phần đồ thị ứng với x ≥ – 3: Đồ thị hàm số g(x) = x + 1 là đường thẳng đi qua hai điểm (0; 1) và (– 1; 0).
   Ta vẽ đồ thị hàm số h(x) = – x – 5 và giữ lại phần đồ thị ứng với x < – 3: Đồ thị hàm số h(x) = – x – 5 là đường thẳng đi qua hai điểm (– 5; 0) và (– 3; – 2).
   Ta được đồ thị của hàm số cần vẽ như hình sau:
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====