Câu hỏi:
Cho một chiếc thang dựa vào tường. Biết độ nghiêng của chiếc thang đó so với mặt đất là 68°, khi đó độ nghiêng của chiếc thang đó so với bức tường là:
A. 55°;
B. 44°;
C. 33°;
D. 22°.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
Ta vẽ tam giác ABC vuông tại A có \(\widehat B = 68^\circ \) để mô tả hình ảnh chiếc thang dựa vào tường như đề bài.
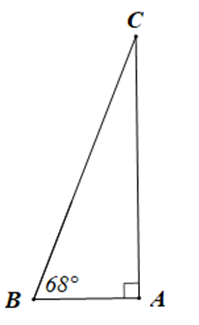
Trong tam giác ABC vuông tại A ta có: \(\widehat B + \widehat C = 90^\circ \) (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra \(\widehat C = 90^\circ – \widehat B = 90^\circ – 68^\circ = 22^\circ \)
Vậy độ nghiêng của chiếc thang so với bức tường là 22°.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có A^=96°,B^=35°. Số đo góc C là:
Câu hỏi:
Cho tam giác ABC có Số đo góc C là:
A. 131°;
B. 61°;
C. 49°;
Đáp án chính xác
D. 41°.
Trả lời:
Đáp án đúng là: C
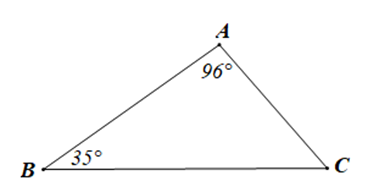
Xét tam giác ABC có (định lí tổng ba góc trong một tam giác)
Suy ra
Mà
Do đó
Vậy số đo góc C là 49°.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình vẽ sau:
Số đo x là:
Câu hỏi:
Cho hình vẽ sau:
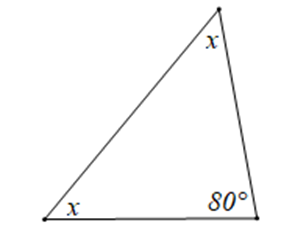
Số đo x là:
A. 40°;
B. 50°;
Đáp án chính xác
C. 60°;
D. 70°.
Trả lời:
Đáp án đúng là: B
Xét tam giác có trong hình vẽ, ta có: x + x + 80° = 180° (tổng ba góc trong một tam giác)
Suy ra 2x = 180° ‒ 80°
Hay 2x = 100°
Do đó x = 100° : 2 = 50°
Vậy x = 50°.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có ba cạnh bằng nhau. Số đo góc A là:
Câu hỏi:
Cho tam giác ABC có ba cạnh bằng nhau. Số đo góc A là:
A. 40°;
B. 50°;
C. 60°;
Đáp án chính xác
D. 70°.
Trả lời:
Đáp án đúng là: C
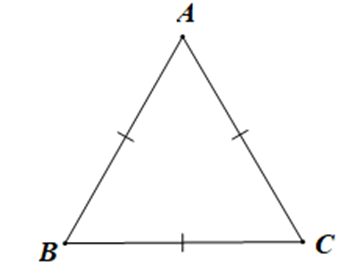
Tam giác ABC có ba cạnh bằng nhau nên là tam giác đều.
Do đó \(\widehat A = \widehat B = \widehat C\)
Mà \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc trong một tam giác)
Suy ra \(\widehat A + \widehat A + \widehat A = 180^\circ \)
Hay \(3\widehat {.A} = 180^\circ \)
Do đó \(\widehat A = 180^\circ :3 = 60^\circ \)
Vậy số đo góc A bằng 60°.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có \(\widehat A = 88^\circ ,\widehat B – \widehat C = 36^\circ .\) Số đo góc B và C lần lượt là:
Câu hỏi:
Cho tam giác ABC có \(\widehat A = 88^\circ ,\widehat B – \widehat C = 36^\circ .\) Số đo góc B và C lần lượt là:
A. 64° và 28°;
Đáp án chính xác
B. 28° và 64°;
C. 62° và 26°;
D. 26° và 62°.
Trả lời:
Đáp án đúng là: A
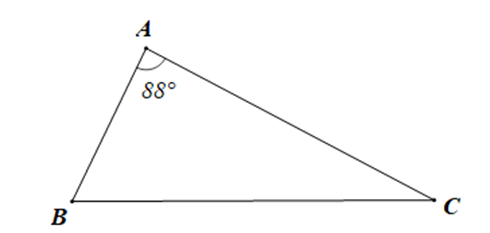
Xét tam giác ABC có (định lí tổng ba góc trong m\(\widehat B + \widehat C = 180^\circ – \widehat A\)ột tam giác)
Suy ra
Hay \(\widehat B + \widehat C = 180^\circ – 88^\circ = 92^\circ \)
Mặt khác \(\widehat B – \widehat C = 36^\circ \)
Suy ra \(\widehat B = \frac{{92^\circ + 36^\circ }}{2} = 64^\circ ,\widehat C = 92^\circ – \widehat B = 92^\circ – 64^\circ = 28^\circ \)
Vậy số đo góc B và C lần lượt là 64° và 28°.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có \(\widehat B = 35^\circ ,\widehat C = 65^\circ .\) Tia phân giác góc A cắt cạnh BC tại D. Số đo góc ADC là:
Câu hỏi:
Cho tam giác ABC có \(\widehat B = 35^\circ ,\widehat C = 65^\circ .\) Tia phân giác góc A cắt cạnh BC tại D. Số đo góc ADC là:
A. 40°;
B. 55°;
C. 60°;
D. 75°.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
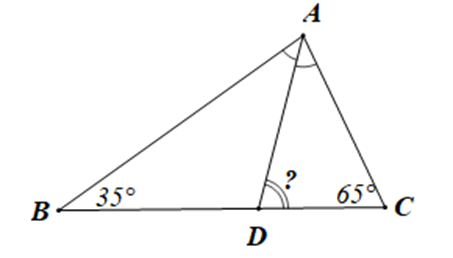
Xét tam giác ABC có \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc trong một tam giác)
Suy ra
Hay \(\widehat A = 180^\circ – 35^\circ – 65^\circ = 80^\circ \)
Mà tia AD là tia phân giác của \(\widehat {BAC}\)
Nên \(\widehat {BAD} = \widehat {CAD} = \frac{1}{2}\widehat {BAC}\) (tính chất tia phân giác của một góc)
Suy ra \(\widehat {BAD} = \widehat {CAD} = \frac{1}{2}.80^\circ = 40^\circ \)
Mặt khác: \(\widehat {ADC}\) là góc ngoài của tam giác ABD tại đỉnh D
Nên \(\widehat {ADC} = \widehat {BAD} + \widehat B\) (tính chất góc ngoài của một tam giác)
Hay \(\widehat {ADC} = 40^\circ + 35^\circ = 75^\circ \)
Vậy số đo góc ADC là 75°.====== **** mời các bạn xem câu tiếp bên dưới **** =====