Câu hỏi:
Cho tam giác ABC có AB = AC = BC, phân giác BD và CE cắt nhau tại O. Chọn phát biểu sai:
A. CE ^ AB;
B. BD ^ CE;
Đáp án chính xác
C. BD ^ AC;
D. \(\widehat {CBD} = \widehat {BCE}.\)
Trả lời:
Đáp án đúng là: B
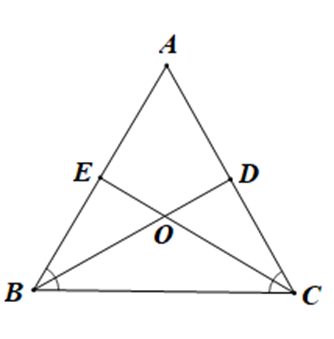
Tam giác ABC có AB = AC = BC (giả thiết) nên là tam giác đều
Do đó \(\widehat A = \widehat {ABC} = \widehat {ACB}\)
CE là tia phân giác của \(\widehat {ACB}\) (giả thiết)
Nên \(\widehat {ACE} = \widehat {ECB} = \frac{1}{2}\widehat {ACB}\) (tính chất tia phân giác) (1)
Xét tam giác ACE và tam giác BCE có:
AC = BC (giả thiết),
\(\widehat {ACE} = \widehat {ECB}\) (chứng minh trên),
CE là cạnh chung
Do đó DACE = DBCE (c.g.c)
Suy ra \(\widehat {AEC} = \widehat {BEC}\) (hai góc tương ứng)
Mà \(\widehat {AEC} + \widehat {BEC} = 180^\circ \) (tính chất hai góc kề bù)
Nên \(\widehat {AEC} = \widehat {BEC} = \frac{{180^\circ }}{2} = 90^\circ \)
Do đó CE ^ AB. Nên A là khẳng định đúng.
Mà BD là tia phân giác của \(\widehat {ABC}\) (giả thiết)
Nên \(\widehat {ABD} = \widehat {DBC} = \frac{1}{2}\widehat {ABC}\) (tính chất tia phân giác) (2)
Xét tam giác ABD và tam giác CBD có:
AB = BC (giả thiết),
\(\widehat {ABD} = \widehat {DBC}\) (chứng minh trên),
BD là cạnh chung
Do đó DABD = DCBD (c.g.c)
Suy ra \(\widehat {ADB} = \widehat {CDB}\) (hai góc tương ứng)
Mà \(\widehat {ADB} + \widehat {CDB} = 180^\circ \) (tính chất hai góc kề bù)
Nên \(\widehat {ADB} = \widehat {CDB} = \frac{{180^\circ }}{2} = 90^\circ \)
Do đó BD ^ AC. Nên B là khẳng định sai và C là khẳng định đúng.
Từ (1) và (2) suy ra \(\widehat {ABD} = \widehat {DBC} = \widehat {ACE} = \widehat {ECB}\). Nên D là khẳng định đúng.
Vậy ta chọn phương án B.
====== **** mời các bạn xem câu tiếp bên dưới **** =====