Câu hỏi:
Cho hình vuông ABCD, trên cạnh AB lấy điểm M, trên cạnh BC lấy điểm N và trên cạnh DC lấy điểm P sao cho AM = BN = CP. Số đo góc MNP là:
A. 60°;
B. 90°;
Đáp án chính xác
C. 100°;
D. 120°.
Trả lời:
Đáp án đúng là: B
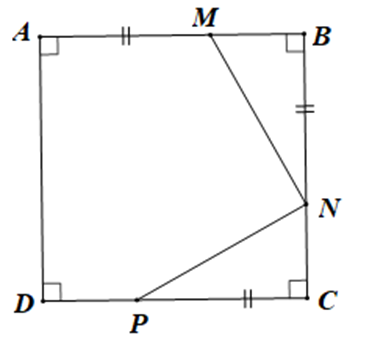
Vì ABCD là hình vuông (giả thiết) nên AB = BC (tính chất hình vuông)
Do đó AM + MB = BN + NC
Mà AM = BN (giả thiết) nên MB = NC.
Xét tam giác MBN và tam giác NCP có:
BN = CP (giả thiết),
\(\widehat B = \widehat C\) (\( = 90^\circ ,\) tính chất hình vuông),
MB = NC (chứng minh trên)
Do đó DMBN = DNCP (c.g.c)
Suy ra \(\widehat {BMN} = \widehat {CNP}\) (hai góc tương ứng)
Mà \(\widehat {BMN} + \widehat {BNM} = 90^\circ \) (trong tam giác BMN vuông tại B, hai góc nhọn phụ nhau)
Do đó \(\widehat {BNM} + \widehat {CNP} = 90^\circ \)
Mặt khác \(\widehat {BNM} + \widehat {MNP} + \widehat {CNP} = 180^\circ \)
Suy ra \(\widehat {MNP} = 180^\circ – \left( {\widehat {BNM} + \widehat {CNP}} \right) = 180^\circ – 90^\circ = 90^\circ \)
Vậy \(\widehat {MNP} = 90^\circ .\)
====== **** mời các bạn xem câu tiếp bên dưới **** =====