b) Lập phương trình tham số của đường trung tuyến AM.

Câu hỏi:

b) Lập phương trình tham số của đường trung tuyến AM.

Trả lời:

b) Ta có M là trung điểm của BC nên toạ độ của M là: M(2; 2).
Đường thẳng AM có vectơ chỉ phương là vectơ $\overrightarrow{u}=\overrightarrow{AM}$ = (1; – 2) nên phương trình tham số của đường thẳng AM là: $\left\{\begin{array}{l}x=1+t\\ y=4-2t\end{array}\right.$ 

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tìm các giá trị của tham số a, b, c để phương trình ax + by + c = 0 có thể biểu diễn được các đường thẳng trong hình đưới đây.
   
   

   Câu hỏi:
   

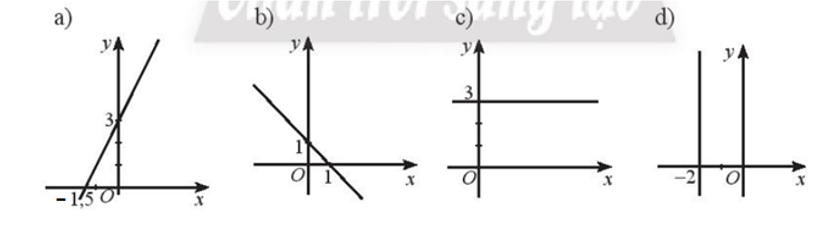
   Tìm các giá trị của tham số a, b, c để phương trình ax + by + c = 0 có thể biểu diễn được các đường thẳng trong hình đưới đây.
   

   Trả lời:

   a) Giả sử đường thẳng cần tìm có dạng y = a’x + b’
   Đường thẳng đi qua điểm $A\left(-\frac{3}{2};0\right)$ ; B(0; 3)
   Ta có hệ $\left\{\begin{array}{l}-\frac{3}{2}a‘+b‘=0\\ 0.a‘+b‘=3\end{array}\right.\iff \left\{\begin{array}{l}a‘=2\\ b‘=3\end{array}\right.$ 
   Suy ra đường thẳng có dạng y = 2x + 3 $\iff$ 2x – y + 3 = 0
   Vì vậy a = 2; b = – 1; c = 3.
   b) Giả sử đường thẳng cần tìm có dạng y = a’x + b’
   Đường thẳng đi qua điểm A(1; 0) ; B(0; 1)
   Ta có hệ $\left\{\begin{array}{l}a‘+b‘=0\\ 0.a‘+b‘=1\end{array}\right.\iff \left\{\begin{array}{l}a‘=-1\\ b‘=1\end{array}\right.$ 
   Suy ra đường thẳng có dạng y = – x + 1 $\iff$ x + y – 1 = 0
   Vì vậy a = 1; b = 1; c = – 1.
   c) Giả sử đường thẳng cần tìm có dạng y = a’x + b’
   Đường thẳng đi qua điểm A(0; 3) và song song với trục hoành nên đường thẳng có dạng y c 3 = 0
   Vì vậy a = 0; b = 1; c = – 3.
   d) Giả sử đường thẳng cần tìm có dạng y = a’x + b’
   Đường thẳng đi qua điểm A(– 2; 0) và song song với trục Oy nên đường thẳng có dạng x + 2 = 0.
   Vì vậy a = 1; b = 0; c = 2.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Lập phương trình tổng quát và phương trình tham số của đường thẳng d trong mỗi trường hợp sau: a) d đi qua điểm M(2; 2) và có vectơ chỉ phương u→ = (4; 7);
   
   

   Câu hỏi:
   

   Lập phương trình tổng quát và phương trình tham số của đường thẳng d trong mỗi trường hợp sau:
   a) d đi qua điểm M(2; 2) và có vectơ chỉ phương $\overrightarrow{u}$ = (4; 7);

   Trả lời:

   a) Đường thẳng d đi qua điểm M(2; 2) và có vectơ chỉ phương $\overrightarrow{u}$ = (4; 7) nên ta có phương trình tham số của đường thẳng d là: 
   $\left\{\begin{array}{l}x=2+4t\\ y=2+7t\end{array}\right.$
   Đường thẳng d đi qua điểm M(2; 2) và có vectơ chỉ phương $\overrightarrow{u}$ = (4; 7) nên vectơ pháp tuyến của đường thẳng d là $\overrightarrow{n}$ (7; –4) phương trình tổng quát của đường thẳng d là: 7(x – 2) – 4(y – 2) = 0 $\iff$ 7x – 4y – 6 = 0

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. b) d đi qua điểm N(0; 1) và có vectơ pháp tuyến là n→= (-5; 3);
   
   

   Câu hỏi:
   

   b) d đi qua điểm N(0; 1) và có vectơ pháp tuyến là $\overrightarrow{n}$= (-5; 3);

   Trả lời:

   b) Đường thẳng d đi qua điểm N(0; 1) và có vectơ pháp tuyến là $\overrightarrow{n}$= (– 5; 3) nên ta có phương trình tổng quát của đường thẳng d là: – 5(x – 0) + 3(y – 1) = 0 ⇔ – 5x + 3y – 3 = 0.
   Đường thẳng d đi qua điểm N(0; 1) và có vectơ pháp tuyến là $\overrightarrow{n}$= (–5 ; 3) nên ta có vectơ chỉ của đường thẳng d là $\overrightarrow{u}$(3; 5) phương trình tham số của đường thẳng d là: $\left\{\begin{array}{l}x=3t\\ y=1+5t\end{array}\right.$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. c) d đi qua A(-2; -3) và có hệ số góc k = 3,
   
   

   Câu hỏi:
   

   c) d đi qua A(-2; -3) và có hệ số góc k = 3,

   Trả lời:

   c) Đường thẳng d đi qua A(–2; –3) và có hệ số góc k = 3 nên phương trình tổng quát của đường thẳng d là: y = 3(x + 2) – 3 ⇔ 3x – y + 3 = 0.
   Khi đó vectơ pháp tuyến của đường thẳng d là $\overrightarrow{n}\left(3;-1\right)$ suy ra vectơ chỉ phương $\overrightarrow{u}(1;3)$. Vì vậy phương trình tham số của đường thẳng d là: $\left\{\begin{array}{l}x=-2+t\\ y=-3+3t\end{array}\right.$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. d) d đi qua hai điểm P(1; 1) và Q(3; 4).
   
   

   Câu hỏi:
   

   d) d đi qua hai điểm P(1; 1) và Q(3; 4).

   Trả lời:

   d) Đường thẳng d đi qua hai điểm P(1; 1) và Q(3; 4) nên vectơ chỉ phương $\overrightarrow{u}=\overrightarrow{PQ}$ = (2; 3) và có vectơ pháp tuyến là vectơ $\overrightarrow{n}$ (3; – 2).
   Phương trình tham số của đường thẳng d là: $\left\{\begin{array}{l}x=1+2t\\ y=1+3t\end{array}\right.$.
   Phương trình tổng quát của đường thẳng d là: 3(x – 1) – 2(y – 1) = 0 $\iff$ 3x – 2y – 1 = 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====