b) Tính khoảng cách thẳng đứng từ một điểm cách chân khung 20 cm lên đến khung thép.

Câu hỏi:

b) Tính khoảng cách thẳng đứng từ một điểm cách chân khung 20 cm lên đến khung thép.

Trả lời:

b)

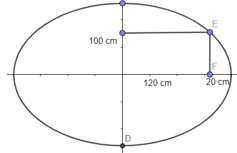
Giả sử thang có hình Elip như hình vẽ
Gọi F là điểm cách chân khung 20 cm.
⇒ OF = 120 – 20 = 100 cm
Suy ra độ dài đoạn FE là khoảng cách cần tìm
Vậy toạ độ của E(100; y); (y > 0)
Vì E thuộc Elip nên ta có $\frac{{100}^2}{14400}+\frac{y^2}{10000}=1\iff$ y² = $\frac{27500}{9}$
$\Rightarrow y=\frac{50\sqrt{11}}{3}$
Vậy $E\left(100;\frac{50\sqrt{11}}{3}\right)$ 
Ta có khoảng cách thẳng đứng từ điểm cách chân khung 20 cm đến khung thép là $\frac{50\sqrt{11}}{3}\approx$  55 cm.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Viết phương trình chính tắc của: a) Elip có trục lớn bằng 12 và trục nhỏ bằng 8;
   
   

   Câu hỏi:
   

   Viết phương trình chính tắc của:
   a) Elip có trục lớn bằng 12 và trục nhỏ bằng 8;

   Trả lời:

   a) Ta có:
   Trục lớn 2a = 12 ⇒ a = 6;
   Trục bé 2b = 8 ⇒ b = 4.
   Vậy phương trình chính tắc của Elip là: $\frac{x^2}{36}+\frac{y^2}{16}=1$ 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. b) Hypebol có tiêu cự 2c = 18 và độ dài trục thực 2a = 14;
   
   

   Câu hỏi:
   

   b) Hypebol có tiêu cự 2c = 18 và độ dài trục thực 2a = 14;

   Trả lời:

   b) Ta có:
   Tiêu cự 2c = 18 ⇒ c = 9
   Trục thực 2a = 14 ⇒ a = 7
   Mặt khác, ta có: b² = c² – a² = 9² – 7² = 32.
   Vậy phương trình chính tắc của Hypebol là: $\frac{x^2}{49}-\frac{y^2}{32}=1$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. c) Parabol có tiêu điểm F(5; 0).
   
   

   Câu hỏi:
   

   c) Parabol có tiêu điểm F(5; 0).

   Trả lời:

   c) Parabol có tiêu điểm F(5; 0) nên ta có $\frac{p}{2}=5$ suy ra p = 10.
   Vậy Parabol có phương trình y² = 20x.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Viết phương trình chính tắc của các đường conic dưới đây. Gọi tên và tìm toạ độ các tiêu điểm của chúng. a) C1:7×2+13y2=1;
   
   

   Câu hỏi:
   

   Viết phương trình chính tắc của các đường conic dưới đây. Gọi tên và tìm toạ độ các tiêu điểm của chúng.
   a) $\left(C_1\right):7x^2+13y^2=1$;

   Trả lời:

   a) $\left(C_1\right):7x^2+13y^2=1$
   $\iff \frac{x^2}{\frac{1}{7}}+\frac{y^2}{\frac{1}{13}}=1$
   Đây là phương trình chính tắc của Elip
   Ta có $a=\frac{\sqrt{7}}{7};b=\frac{\sqrt{13}}{13}$  và c = $\sqrt{a^2-b^2}=\sqrt{\frac{1}{7}-\frac{1}{13}}=\frac{\sqrt{546}}{91}$ 
   Các tiêu điểm $F_1\left(-\frac{\sqrt{546}}{91};0\right);F_2\left(\frac{\sqrt{546}}{91};0\right)$ 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. b) C2:25×2−9y2=225
   
   

   Câu hỏi:
   

   b) $\left(C_2\right):25x^2-9y^2=225$

   Trả lời:

   b) (C₂): 25x² – 9y² = 225
   $\iff \frac{x^2}{9}-\frac{y^2}{25}=1$ 
   $\iff \frac{x^2}{3^2}-\frac{y^2}{5^2}=1$
   Đây là phương trình chính tắc của Hypebol
   Ta có a = 3; b = 5 và c² = a² + b² = 3² + 5² = 34.
   Các tiêu điểm $F_1=\left(-\sqrt{34};0\right),F_2\left(\sqrt{34};0\right)$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====