Khi sử dụng phương pháp quy nạp để chứng minh mệnh đề chứa biến A(n) đúng với mọi giá trị nguyên n≥p với p là số nguyên dương ta sẽ tiến hành 2 bước Bước 1 (bước cơ sở). Chứng minh rằng A(n) đúng khi n=1 Bước 2 (bước quy nạp). Với số nguyên dương tùy ý k, ta giả sử A(n) đúng khi n=k (theo giả thiết quy nạp). Ta sẽ chứng minh rằng A(n) đúng khi n=k+1 Hãy chọn câu trả lời đúng tương ứng với lí luận trên.

Câu hỏi:

Khi sử dụng phương pháp quy nạp để chứng minh mệnh đề chứa biến A(n) đúng với mọi giá trị nguyên $\mathrm{n}\ge \mathrm{p}$ với p là số nguyên dương ta sẽ tiến hành 2 bước
Bước 1 (bước cơ sở). Chứng minh rằng A(n) đúng khi n=1
Bước 2 (bước quy nạp). Với số nguyên dương tùy ý k, ta giả sử A(n) đúng khi n=k (theo giả thiết quy nạp). Ta sẽ chứng minh rằng A(n) đúng khi n=k+1
Hãy chọn câu trả lời đúng tương ứng với lí luận trên.

A. Chỉ có bước 2 đúng.

B. Cả hai bước đều đúng.

C. Cả hai bước đều sai.

Đáp án chính xác

D. Chỉ có bước 1 đúng.

Trả lời:

Chọn C
Bước 1 sai, vì theo bài toán $\mathrm{n}\ge \mathrm{p}$ nên ta phải chứng minh rằng A(n) đúng khi n=p.
Bước 2 sai, không thể “Với số nguyên dương tùy ý k” mà phải là “Với số nguyên dương $\mathrm{k}\ge \mathrm{p}$”.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Chứng minh rằng với mọi số tự nhiên n≥2, ta luôn có 2n+1>2n+3        (*)
   
   

   Câu hỏi:
   

   Chứng minh rằng với mọi số tự nhiên $\mathrm{n}\ge 2$, ta luôn có $2^{n+1}>2n+3(*)$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Chứng minh rằng với mọi số nguyên dương n, ta có 1.4+2.7+…+n(3n+1)=nn+12        (1)
   
   

   Câu hỏi:
   

   Chứng minh rằng với mọi số nguyên dương n, ta có $1.4+2.7+\mathrm{\dots }+n(3n+1)=n{\left(n+1\right)}^2\left(1\right)$

   Trả lời:

   
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Chứng minh rằng với mọi số nguyên dương n≥2 , ta có 1.22+2.33+3.44+…+n−1n2=nn2−13n+212      (1)
   
   

   Câu hỏi:
   

   Chứng minh rằng với mọi số nguyên dương $\mathrm{n}\ge 2$ , ta có ${1.2}^2+{2.3}^3+{3.4}^4+\mathrm{\dots }+\left(n-1\right)n^2=\frac{n\left(n^2-1\right)\left(3n+2\right)}{12}\left(1\right)$

   Trả lời:

   
   

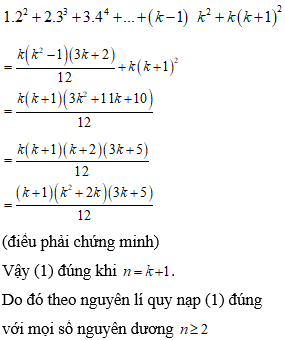
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Chứng minh rằng với mọi số nguyên dương n, ta có 11.2.3+12.3.4+…+1nn+1n+2=nn+34n+1n+2     (1)
   
   

   Câu hỏi:
   

   Chứng minh rằng với mọi số nguyên dương n, ta có $\frac{1}{\mathrm{1.2.3}}+\frac{1}{\mathrm{2.3.4}}+\mathrm{\dots }+\frac{1}{n\left(n+1\right)\left(n+2\right)}=\frac{n\left(n+3\right)}{4\left(n+1\right)\left(n+2\right)}\left(1\right)$

   Trả lời:

   
   

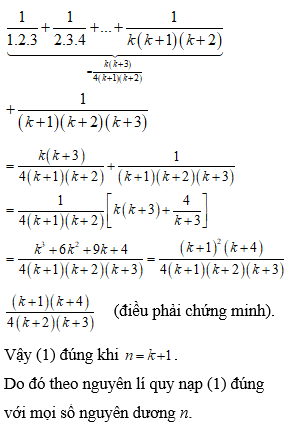
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Chứng minh rằng với mọi số nguyên dương n≥2  ta có 1n+1+1n+2+…+1n+n>1324     (1)
   
   

   Câu hỏi:
   

   Chứng minh rằng với mọi số nguyên dương $\mathrm{n}\ge 2$  ta có $\frac{1}{n+1}+\frac{1}{n+2}+\mathrm{\dots }+\frac{1}{n+n}>\frac{13}{24}\left(1\right)$

   Trả lời:

   
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====