b) x−2y≤33x+2y≥9x+y≤6x≥1

Câu hỏi:

b) $\left\{\begin{array}{l}x-2y\le 3\\ 3x+2y\ge 9\\ x+y\le 6\\ x\ge 1\end{array}\right.$

Trả lời:

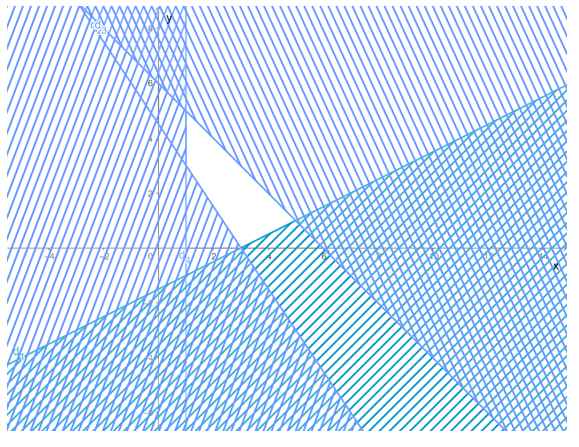
 b) Vẽ các đường thẳng:
d₁: x – 2y = 3 là đường thẳng đi qua hai điểm có tọa độ là (3; 0) và (1; – 1).
d₂: 3x + 2y = 9 là đường thẳng đi qua hai điểm (3; 0) và (1; 3).
d₃: x + y = 6 là đường thẳng đi qua hai điểm (6; 0) và (0; 6).
d₄: x + y = 6 là đường thẳng song song với trục tung Oy và đi qua điểm (1; 0).
Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình trong hệ ta được miền nghiệm của hệ bất phương trình là miền không bị gạch chéo trong hình dưới đây:

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cặp số nào sau đây không là nghiệm của bất phương trình x – 2y ≥ 5?
   
   

   Câu hỏi:
   

   Cặp số nào sau đây không là nghiệm của bất phương trình x – 2y ≥ 5?

   A. (3; – 1);

   B. (– 1; 4);

   Đáp án chính xác

   C. (2; – 3);

   D. (1; – 2).

   Trả lời:

   Đáp án đúng là B
   +) Thay x = 3, y = – 1 vào bất phương trình x – 2y ≥ 5, ta được:
   3 – 2.(– 1) ≥ 5 ⇔ 5 ≥ 5 (luôn đúng)
   Do đó cặp số (3; – 1) là nghiệm của bất phương trình đã cho.
   +) Thay x = – 1, y = 4 vào bất phương trình x – 2y ≥ 5, ta được:
   3.(– 1) – 2.4 ≥ 5 ⇔ – 11 ≥ 5 (vô lí)
   Do đó cặp số (– 1; 4) không là nghiệm của bất phương trình đã cho.
   +) Thay x = 2, y = – 3 vào bất phương trình x – 2y ≥ 5, ta được:
   3.2 – 2.(– 3) ≥ 5 ⇔ 15 ≥ 5 (luôn đúng)
   Do đó cặp số (2; – 3) là nghiệm của bất phương trình đã cho.
   +) Thay x = 1, y = – 2 vào bất phương trình x – 2y ≥ 5, ta được:
   3.1 – 2.(– 2) ≥ 5 ⇔ 7 ≥ 5 (luôn đúng)
   Do đó cặp số (1; – 2) là nghiệm của bất phương trình đã cho.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cặp số nào sau đây không là nghiệm của hệ bất phương trình x−2y>42x+y>6.
   
   

   Câu hỏi:
   

   Cặp số nào sau đây không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x-2y>4\\ 2x+y>6\end{array}\right.$.

   A. (2; – 1);

   Đáp án chính xác

   B. (7; 1);

   C. (5; – 1);

   D. (6; – 2).

   Trả lời:

   Đáp án đúng là A
   Ta xét hệ bất phương trình: $\left\{\begin{array}{l}x-2y>4\left(1\right)\\ 2x+y>6\left(2\right)\end{array}\right.$
   +) Thay x = 2 và y = – 1 vào từng bất phương trình của hệ ta được:
   (1) ⇔ 2 – 2(– 1) > 4 ⇔ 4 > 4 (vô lí);
   (2) ⇔ 2.2 + (– 1) > 6 ⇔ 3 > 6 (vô lí).
   Do đó cặp số (2; – 1) không là nghiệm của hệ bất phương trình đã cho.
   +) Thay x = 7 và y = 1 vào từng bất phương trình của hệ ta được:
   (1) ⇔ 7 – 2.1 > 4 ⇔ 5 > 4 (luôn đúng);
   (2) ⇔ 2.7 + 1 > 6 ⇔ 15 > 6 (luôn đúng).
   Do đó cặp số (7; 1) là nghiệm của hệ bất phương trình đã cho.
   +) Thay x = 5 và y = – 1 vào từng bất phương trình của hệ ta được:
   (1) ⇔ 5 – 2(– 1) > 4 ⇔ 7 > 4 (luôn đúng);
   (2) ⇔ 2.5 + (– 1) > 6 ⇔ 9 > 6 (luôn đúng).
   Do đó cặp số (5; – 1) là nghiệm của hệ bất phương trình đã cho.
   +) Thay x = 6 và y = – 2 vào từng bất phương trình của hệ ta được:
   (1) ⇔ 6 – 2(– 2) > 4 ⇔ 10 > 4 (luôn đúng);
   (2) ⇔ 2.6 + (– 2) > 6 ⇔ 10 > 6 (luôn đúng).
   Do đó cặp số (6; – 2) là nghiệm của hệ bất phương trình đã cho.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Phần không bị gạch (kể cả d) ở Hình 11 là miền nghiệm của bất phương trình:
   
   

   Câu hỏi:
   

   Phần không bị gạch (kể cả d) ở Hình 11 là miền nghiệm của bất phương trình:
   

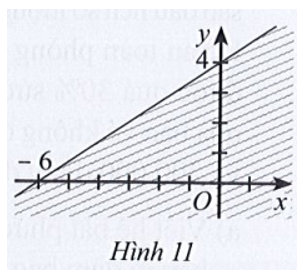
   A. 2x – 3y ≤ – 12;

   Đáp án chính xác

   B. 2x – 3y ≥ – 12;

   C. 3x – 2y ≤ 12;

   D. 3x – 2y ≥ 12.

   Trả lời:

   Đáp án đúng là A
   Gọi đường thẳng d có dạng: y = ax + b (a
   Đường thẳng này cắt hai trục Ox và Oy lần lượt tại các điểm có tọa độ ( – 6; 0) và (0; 4) nên ta có phương trình là: $\frac{x}{-6}+\frac{y}{4}=1\iff 2x-3y=-12$.
   Lấy điểm O(0; 0) có 2.0 – 3.0 = 0 > – 12, mà điểm O không thuộc miền nghiệm của hệ bất phương trình đã cho và miền nghiệm kể cả d do đó bất phương trình cần tìm là 2x – 3y ≤ – 12.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Phần không bị gạch (kể cả tia AB, AC) ở Hình 12 là miền nghiệm của hệ bất phương trình:
   
   

   Câu hỏi:
   

   Phần không bị gạch (kể cả tia AB, AC) ở Hình 12 là miền nghiệm của hệ bất phương trình:
   

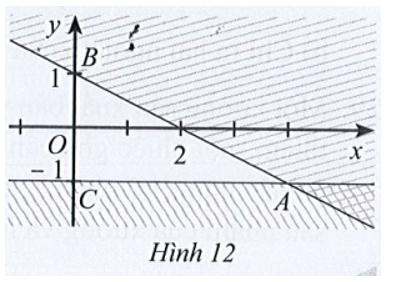
   A. $\left\{\begin{array}{l}x+2y\ge 2\\ y\ge -1.\end{array}\right.$

   B. $\left\{\begin{array}{l}x+2y\le 2\\ y\ge -1.\end{array}\right.$

   Đáp án chính xác

   C. $\left\{\begin{array}{l}x+2y<2\\ y>-1.\end{array}\right.$

   D. $\left\{\begin{array}{l}x+2y>2\\ y>-1.\end{array}\right.$

   Trả lời:

   Đáp án đúng là B
   Gọi d là đường thẳng đi qua hai điểm A và B, vì đường thẳng này cắt hai trục tọa độ Ox, Oy lần lượt tại các điểm có tọa độ là (2; 0) và (0; 1) nên có phương trình là: $\frac{x}{2}+\frac{y}{1}=1\iff x+2y=2$.
   Lấy O(0; 0) có 0 + 2.0 = 0 < 2 và điểm O thuộc miền nghiệm của hệ bất phương trình và miền nghiệm kể cả đường thẳng d nên ta có bất phương trình x + 2y ≤ 2 (1).
   Gọi d’ là đường thẳng đi qua hai điểm A và C và song song với trục hoành Ox nên có phương trình y = – 1.
   Lấy điểm O(0; 0) có 0 > – 1 và điểm O thuộc miền nghiệm của hệ bất phương trình và miền nghiệm kể cả đường thẳng d nên ta có bất phương trình y ≥ – 1 (2).
   Từ (1) và (2) ta có hệ bất phương trình $\left\{\begin{array}{l}x+2y\le 2\\ y\ge -1\end{array}\right.$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Giá trị nhỏ nhất của biểu thức F = – 2x + y trên miền nghiệm của hệ bất phương trình x−y≥−2x+y≤4x−5y≤−2là:
   
   

   Câu hỏi:
   

   Giá trị nhỏ nhất của biểu thức F = – 2x + y trên miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x-y\ge -2\\ x+y\le 4\\ x-5y\le -2\end{array}\right.$là:

   A. – 5.

   B. – 7.

   C. 1

   D. 4

   Trả lời:

   Đáp án đúng là A
   Xác định miền nghiệm của hệ bất phương trình như sau:
   – Vẽ ba đường thẳng:
   Đường thẳng d₁: x – y = – 2 cắt trục Ox, Oy lần lượt tại các điểm có tọa độ (– 2; 0) và (0; 2).
   Đường thẳng d₂: x + y = 4 cắt trục Ox, Oy lần lượt tại các điểm có tọa độ (4; 0) và (0; 4).
   Đường thẳng d₃: x – 5y = – 2 lần lượt đi qua các điểm có tọa độ (– 2; 0) và (3; 1).
   – Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình. Miền nghiệm của hệ bất phương trình là miền trong tam giác ABC với A( – 2; 0), B(1; 3) và C(3; 1) như hình vẽ sau:
   

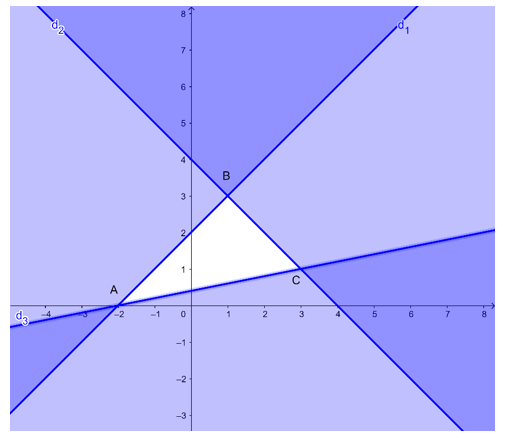
   Ta có biểu thức F = – 2x + y có giá trị nhỏ nhất tại một trong các đỉnh của tam giác ABC.
   Tính giá trị biểu thức T tại các đỉnh của tứ giác:
   Tại A(– 2; 0), với x = – 2 và y = 0 thì F = – 2.(– 2) + 0 = 4;
   Tại B(1; 3), với x = 1 và y = 3 thì F = – 2.1 + 3 = 1;
   Tại C(3; 1), với x = 3 và y = 1 thì F = – 2.3 + 1 = – 5 ;
   Ta được F đạt giá trị nhỏ nhất bằng – 5 khi x = 3, y = 1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====