Trong bài toán ứng dụng, khi chơi trên sân cầu lông đơn, các lần phát cầu với thông tin như sau có được cho là hợp lệ không? (Các thông tin không được đề cập thì vẫn giữ như trong giả thiết bài toán trên). a) Vận tốc xuất phát của cầu là 12m/s. b) Vị trí phát cầu cách mặt đất là 1,3m. Lưu ý: Các thông số về sân cầu lông được cho trong Hình 11.

Câu hỏi:

Trong bài toán ứng dụng, khi chơi trên sân cầu lông đơn, các lần phát cầu với thông tin như sau có được cho là hợp lệ không? (Các thông tin không được đề cập thì vẫn giữ như trong giả thiết bài toán trên).
a) Vận tốc xuất phát của cầu là 12m/s.
b) Vị trí phát cầu cách mặt đất là 1,3m.
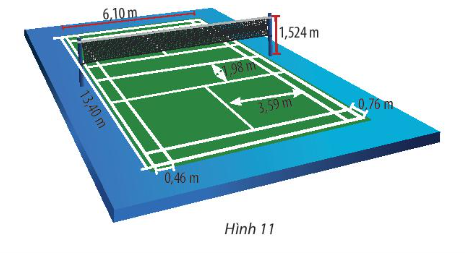
Lưu ý: Các thông số về sân cầu lông được cho trong Hình 11.

Trả lời:

Ta có hình vẽ sau

a) Theo đề bài, ta có:
g ≈ 9,8 m/s², α = 30°, v₀ = 12m/s, y₀ = 0,7 m.
Khi đó, ta có hàm số: y = $\frac{-49}{1080}{x}^2+\frac{\sqrt{3}}{3}x+0,7$.
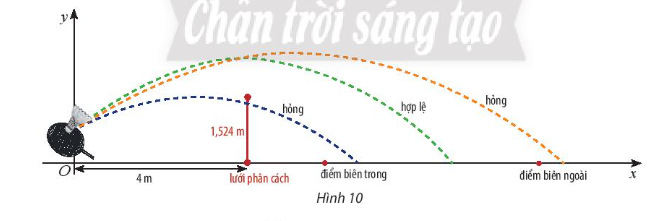
Khi cầu bay tới vị trí lưới phân cách, nếu nó ở bên trên mặt lưới và điểm rơi không ra khỏi đường biên phía bên sân đối phương thì lần phát cầu mới được xem là hợp lệ.
Ta cần so sánh tung độ của điểm quỹ đạo (có hoành độ bằng khoảng cách từ gốc tọa độ đến chân lưới phân cách) với chiều cao mép lưới.
Khi x = 4 (do người đứng cách lưới 4m) ta có:
y =$\frac{-49}{1080}{.4}^2+\frac{\sqrt{3}}{3}.4+0,7\approx 2,28>1,524$.
Như vậy lần phát cầu này thỏa mãn qua lưới.
Vị trí cầu rơi chạm đất là giao điểm của Parabol với trục hoành nên giải phương trình:
$\frac{-49}{1080}{x}^2+\frac{\sqrt{3}}{3}x+0,7=0$ ta được x₁ ≈ 13,84 và x₂ ≈ -1,11.
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 13,84m.
Ta có:
Điểm bên trong sẽ cách vị trí phát: 4 + 1,98 = 5, 98m.
Điểm bên ngoài sẽ cách vị trí phát: 4 + 6,7 = 10,7 m.
Do vị trí điểm rơi nằm ngoài khoảng giữa điểm trong và điểm ngoài nên lần phát cầu này hỏng.
Vậy với vận tốc xuất phát của cầu là 12m/s thì lần phát này hỏng (không hợp lệ).
b) Theo đề bài, ta có:
g ≈ 9,8 m/s², α = 30°, v₀ = 8m/s, y₀ = 1,3 m.
Khi đó, ta có hàm số: y = $\frac{-49}{480}{x}^2+\frac{\sqrt{3}}{3}x+1,3$.
Khi cầu bay tới vị trí lưới phân cách, nếu nó ở bên trên mặt lưới và điểm rơi không ra khỏi đường biên phía bên sân đối phương thì lần phát cầu mới được xem là hợp lệ.
Ta cần so sánh tung độ của điểm quỹ đạo (có hoành độ bằng khoảng cách từ gốc tọa độ đến chân lưới phân cách) với chiều cao mép lưới.
Khi x = 4 (do người đứng cách lưới 4m) ta có:
y =$\frac{-49}{480}{.4}^2+\frac{\sqrt{3}}{3}.4+1,3\approx 1,98>1,524$.
Như vậy lần phát cầu này thỏa mãn qua lưới.
Vị trí cầu rơi chạm đất là giao điểm của Parabol với trục hoành nên giải phương trình:
$\frac{-49}{480}{x}^2+\frac{\sqrt{3}}{3}x+1,3=0$ ta được x₁ ≈ 7,38 và x₂ ≈ -1,73.
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 7,38m.
Ta có:
Điểm bên trong sẽ cách vị trí phát: 4 + 1,98 = 5, 98m.
Điểm bên ngoài sẽ cách vị trí phát: 4 + 6,7 = 10,7 m.
Do vị trí điểm rơi nằm trong khoảng giữa điểm trong và điểm ngoài nên lần phát cầu này hợp lệ.
Vậy với vị trí phát cầu cách mặt đất 1,3m thì lần phát cầu này hợp lệ.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Các hàm số này có chung đặc điểm gì? y = ax2; y = a(x – m)(x – n); y = ax2 + bx; y = a(x – h)2 + k; y = ax2 + bx + c.
   
   

   Câu hỏi:
   

   Các hàm số này có chung đặc điểm gì?
   y = ax²;
   y = a(x – m)(x – n);
   y = ax² + bx;
   y = a(x – h)² + k;
   y = ax² + bx + c.

   Trả lời:

   Ta có:
   y = a(x – m)(x – n) = ax² – a(m + n)x + a.m.n.
   y = a(x – h)² + k = ax² – 2ahx + ah² + k.
   Các hàm số đã cho đều là các hàm số bậc hai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Khai triển biểu thức của các hàm số sau và sắp xếp theo thứ tự lũy thừa của x giảm dần (nếu có thể). Hàm số nào có lũy thừa bậc cao nhất của x là bậc hai? a) y = 2x(x – 3); b) y = x(x2 + 2) – 5; c) y = -5(x + 1)(x – 4).
   
   

   Câu hỏi:
   

   Khai triển biểu thức của các hàm số sau và sắp xếp theo thứ tự lũy thừa của x giảm dần (nếu có thể). Hàm số nào có lũy thừa bậc cao nhất của x là bậc hai?
   a) y = 2x(x – 3);
   b) y = x(x² + 2) – 5;
   c) y = -5(x + 1)(x – 4).

   Trả lời:

   a) Xét hàm số: y = 2x(x – 3) = 2x² – 6x.
   Bậc cao nhất của hàm số là bậc hai.
   b) Xét hàm số: y = x(x² + 2) – 5 = x³ + 2x – 5.
   Bậc cao nhất của hàm số là bậc ba.
   c) y = -5(x + 1)(x – 4) = – 5x²  + 15x + 20.
   Bậc cao nhất của hàm số là bậc hai.
   Vậy hàm số ở ý a) và c) là các số có lũy thừa bậc cao nhất của x là bậc hai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Hàm số nào trong các hàm số đã cho ở hoạt động khám phá 1 là hàm số bậc hai?
   
   

   Câu hỏi:
   

   Hàm số nào trong các hàm số đã cho ở hoạt động khám phá 1 là hàm số bậc hai?

   Trả lời:

   Các hàm số ở hoạt động khám phá 1:
   a) y = 2x(x – 3) = 2x² – 6x là hàm số bậc hai với a = 2, b = – 6, c = 0.
   b) y = x(x² + 2) – 5 = x³ + 2x – 5 không là hàm số bậc hai
   c) y = -5(x + 1)(x – 4) = – 5x²  + 15x + 20 là hàm số bậc hai với a = -5, b = 15, c = 20.
   Vậy hàm số ở ý a) và c) là các hàm số bậc hai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
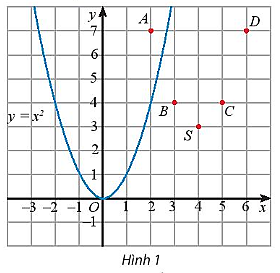
4. a) Xét hàm số: y = f(x) = x2 – 8x + 19 = (x – 4)2 + 3 có bảng giá trị: x 2 3 4 5 6 f(x) 7 4 3 4 7 Trên mặt phẳng tọa độ, ta có các điểm (x; f(x)) với x thuộc bảng giá trị đã cho (Hình 1). Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị của hàm số y = x2 trên Hình 1. 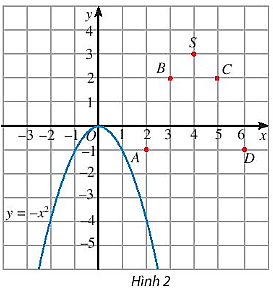b) Tương tự, xét hàm số: y = g(x) = – x2 + 8x – 13 = – (x – 4)2 + 3 có bảng giá trị: x 2 3 4 5 6 g(x) -1 2 3 2 -1 Trên mặt phẳng tọa độ, ta có các điểm (x; g(x)) với x thuộc bảng giá trị đã cho (Hình 2). Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số y = – x2 trên Hình 2.
   
   

   Câu hỏi:
   

   a) Xét hàm số: y = f(x) = x² – 8x + 19 = (x – 4)² + 3 có bảng giá trị:

   x

   2

   3

   4

   5

   6

   f(x)

   7

   4

   3

   4

   7

   Trên mặt phẳng tọa độ, ta có các điểm (x; f(x)) với x thuộc bảng giá trị đã cho (Hình 1).
   Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị của hàm số y = x² trên Hình 1.
   

   b) Tương tự, xét hàm số: y = g(x) = – x² + 8x – 13 = – (x – 4)² + 3 có bảng giá trị:

   x

   2

   3

   4

   5

   6

   g(x)

   -1

   2

   3

   2

   -1

   Trên mặt phẳng tọa độ, ta có các điểm (x; g(x)) với x thuộc bảng giá trị đã cho (Hình 2).
   Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số y = – x² trên Hình 2.
   

   Trả lời:

   a) Đường cong đi qua các điểm A, B, S, C, D là đường cong màu đỏ trên hình vẽ:
   

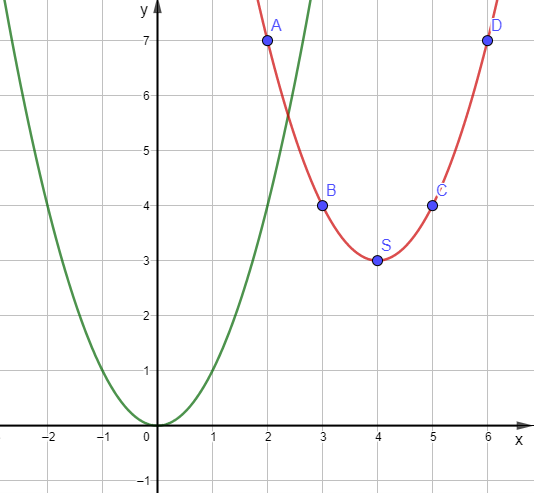
   Nhận xét:
   Về hình dáng của đường cong màu đỏ giống với hình dáng của đường cong màu xanh là một đường cong parabol.
   – Có đỉnh là điểm S với hoành độ là 4 và tung độ là 3.
   – Có trục đối xứng là đường thẳng x = 4 (đường thẳng này đi qua đỉnh S và song song với trục Oy).
   – Bề lõm của đồ thị hướng lên trên.
   b) ) Đường cong đi qua các điểm A, B, S, C, D là đường cong màu cam trên hình vẽ:
   

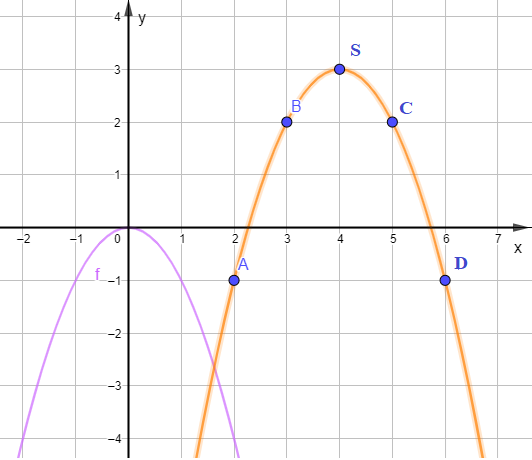
   Nhận xét:
   Về hình dáng của đường cong màu cam giống với hình dáng của đường cong màu tím là một đường cong parabol.
   – Có đỉnh là điểm S với hoành độ là 4 và tung độ là 3.
   – Có trục đối xứng là đường thẳng x = 4 (đường thẳng này đi qua đỉnh S và song song với trục Oy).
   – Bề lõm của đồ thị hướng xuống dưới.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Vẽ đồ thị hàm số y = x2 – 4x + 3 rồi so sánh đồ thị hàm số này với đồ thị hàm số ở ví dụ 2a. Nếu nhận xét về hai đồ thị này.
   
   

   Câu hỏi:
   

   Vẽ đồ thị hàm số y = x² – 4x + 3 rồi so sánh đồ thị hàm số này với đồ thị hàm số ở ví dụ 2a. Nếu nhận xét về hai đồ thị này.

   Trả lời:

   Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = x² – 4x + 3 là một parabol (P):
   – Có đỉnh S với hoàng độ x_S = 2, tung độ y_S = -1;
   – Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
   – Bề lõm quay lên trên vì a = 1 > 0;
   – Cắt trục tung tại điểm có tung độ y = 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
   

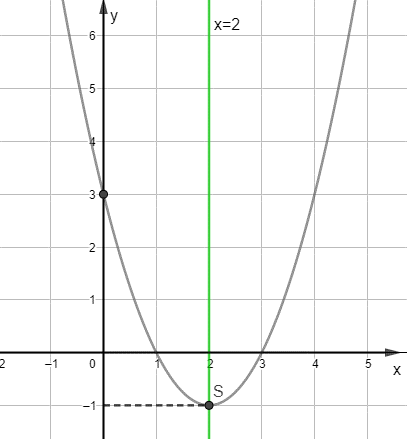
   So với đồ thị của hàm số ở ví dụ 2 a) ta thấy:
   – Hai đồ thị đều là đường cong parabol.
   – Hai đồ thị có cùng trục đối xứng x = 2.
   – Đồ thị ở ví dụ 2a) có bề lõm hướng xuống dưới, còn đồ thị hàm số này có bề lõm hướng lên trên.
   – Hai tọa độ đỉnh của hai đồ thị hàm số đối xứng qua trục Ox.
   – Giao điểm của đồ thị hàm số ở ví dụ 2a) với trục tung đối xứng với giao điểm của đồ thị hàm số này với trục tung.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====