Chứng minh rằng với mọi góc α (0° ≤ α  ≤ 180°), ta đều có: a) cos2α  + sin2α  = 1; b) tanα  . cotα  = 1 (0° < α  < 180°, α  ≠ 90°). c) 1 + tan2α  = 1cos2α  (α  ≠ 90°); d) 1 + cot2 α  = 1sin2α  (0° < α  < 180°).

Câu hỏi:

Chứng minh rằng với mọi góc α (0° ≤ α  ≤ 180°), ta đều có:
a) cos²α  + sin²α  = 1;
b) tanα  . cotα  = 1 (0° < α  < 180°, α  ≠ 90°).
c) 1 + tan²α  = $\frac{1}{{\cos }^2\alpha }$  (α  ≠ 90°);
d) 1 + cot² α  = $\frac{1}{{\sin }^2\alpha }$  (0° < α  < 180°).

Trả lời:

a) Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x₀; y₀) là điểm trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=\alpha$ .

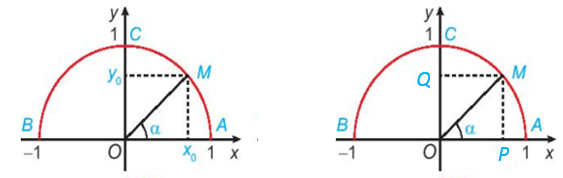
Gọi P, Q tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Áp dụng định lý Pythagore cho tam giác OPM vuông tại P có cạnh huyền OM = 1.
Ta có: OP² + MP² = OM²
Mà OP = |x₀| ; MP = OQ = y₀ và OM = 1
Suy ra : |x₀|² + y₀² = 1 tức là x₀² + y₀² = 1 (vì |x₀|² = x₀²)
Mặt khác, theo định nghĩa giá trị lượng giác của một góc ta có:

sinα = y₀
cosα = x₀
Suy ra cos² α + sin ² α  = x₀² + y₀² = 1
Vậy sin ² α + cos² α = 1.
b) Với mỗi góc α (0° < α  < 180°, α  ≠ 90°), gọi M(x₀; y₀) là điểm trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=\alpha$ .
Khi đó tanα  = $\frac{y_0}{x_0}$  ; cotα = $\frac{x_0}{y_0}$ ;
Suy ra tanα  . cotα  = $\frac{y_0}{x_0}$. $\frac{x_0}{y_0}$ = 1.
Vậy tanα  . cotα  = 1 (0° < α  < 180°, α  ≠ 90°).
c) Với α  ≠ 90° ; tanα =  và x₀² + y₀² = sin ²α + cos²α = 1 ; cosα = x₀ ⇒ cos²α = x₀².
Ta có: 1 + tan²α  =
$1+{\left(\frac{y_0}{x_0}\right)}^2=1+\frac{{y_0}^2}{x20}=\frac{{x_0}^2+{y_0}^2}{x20}=\frac{1}{x20}=\frac{1}{{\cos }^2\alpha }$ .
Vậy 1 + tan²α  = $\frac{1}{{\cos }^2\alpha }$  (α  ≠ 90°).
d) Với 0° < α  < 180° ta có cotα = $\frac{x_0}{y_0}$ và sinα = y₀ ⇒ sin² α = y₀².
Ta có : 1 + cot²α =
$1+{\left(\frac{x_0}{y_0}\right)}^2=1+\frac{{x_0}^2}{{y_0}^2}=\frac{{x_0}^2+{y_0}^2}{{y_0}^2}=\frac{1}{{y_0}^2}=\frac{1}{{\sin }^2\alpha }$ .
Vậy 1 + cot² α  = $\frac{1}{{\sin }^2\alpha }$  (0^o < α  < 180°).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Làm thế nào để mở rộng khái niệm tỉ số lượng giác của góc nhọn cho các góc từ 0° đến 180°?
   
   

   Câu hỏi:
   

   Làm thế nào để mở rộng khái niệm tỉ số lượng giác của góc nhọn cho các góc từ 0° đến 180°?

   Trả lời:

   Để mở rộng khái niệm tỉ số lượng giác của góc nhọn cho góc từ 0° đến 180° ta thực hiện như sau:
   Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho . Gọi (x₀; y₀) là tọa độ của điểm M, ta có:
   + sin của góc α là tung độ y₀ của điểm M, được kí hiệu là sinα;
   + côsin của góc α là hoành độ x₀ của điểm M, được kí hiệu là cosα;
   + tang của α là tỉ số  (x₀ ≠ 0), được kí hiệu là tanα = $\frac{y_0}{x_0}$ ;
   + côtang của α là tỉ số (y₀ ≠ 0), được kí hiệu là cotα = $\frac{x_0}{y_0}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn α, lấy điểm M trên nửa đường tròn đơn vị sao cho . Giả sử điểm M có tọa độ (x0; y0). Áp dụng cách tính tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng: sinα = y0; cosα = x0 ; tanα = y0x0  ; cotα =x0y0 .
   
   

   Câu hỏi:
   

   Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn α, lấy điểm M trên nửa đường tròn đơn vị sao cho . Giả sử điểm M có tọa độ (x₀; y₀). Áp dụng cách tính tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:
   sinα = y₀; cosα = x₀ ; tanα = $\frac{y_0}{x_0}$  ; cotα =$\frac{x_0}{y_0}$ .
   

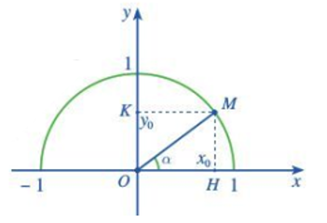
   Trả lời:

   Trong tam giác HOM vuông tại H có cạnh huyền OM = 1:
   Ta có, sinα = sin$\widehat{HOM}$ = $\frac{MH}{OM}$  = $\frac{y_0}{1}=y_0$ ;
   cosα = cos$\widehat{HOM}$  =$\frac{OH}{OM}$ = $\frac{x_0}{1}=x_0$ ;
   tanα = $\frac{MH}{OH}$  = $\frac{y_0}{x_0}$ ;
   cotα  = $\frac{OH}{MH}$  = $\frac{x_0}{y_0}$.
   Vậy sinα  = y₀; cosα  = x₀ ; tanα  = $\frac{y_0}{x_0}$  ; cotα =$\frac{x_0}{y_0}$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tìm các giá trị lượng giác của góc 135°.
   
   

   Câu hỏi:
   

   Tìm các giá trị lượng giác của góc 135°.

   Trả lời:

   

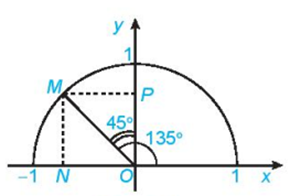
   Gọi M là điểm trên nửa đường tròn đơn vị sao cho$\widehat{xOM}={135}^o$ . Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
   Vì  $\widehat{xOM}={135}^o$nên $\widehat{MOP}={45}^o$ , $\widehat{MON}={45}^o$ .
   Tam giác MOP là tam giác vuông cân với cạnh huyền OM = 1.
   cos $\widehat{MOP}$ = cos45° = $\frac{OP}{OM}$ =$\frac{OP}{1}=OP$
   Mà cos45° = $\frac{\sqrt{2}}{2}$ .
   Do đó: OP = $\frac{\sqrt{2}}{2}$ .
   Tam giác MON vuông tại N có góc $\widehat{MON}={45}^o$  và cạnh huyền OM = 1
   cos $\widehat{MON}$ = cos 45° = $\frac{ON}{OM}$ =$\frac{ON}{1}=ON$
   Mà cos45° = $\frac{\sqrt{2}}{2}$ . Do đó: ON = $\frac{\sqrt{2}}{2}$ .
   Mặt khác, do điểm M nằm bên trái trục tung nên $M\left(-\frac{\sqrt{2}}{2};\frac{\sqrt{2}}{2}\right)$ .
   Vậy theo định nghĩa ta có:
   sin135° = $\frac{\sqrt{2}}{2}$  ;
   cos135° = $-\frac{\sqrt{2}}{2}$ ;
   tan135° =  – 1;
   cot135° =  – 1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4). Tính tổng số đo của hai góc xOM^  và xON^ . 
   
   

   Câu hỏi:
   

   Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4). Tính tổng số đo của hai góc $\widehat{xOM}$  và $\widehat{xON}$ .
    
   

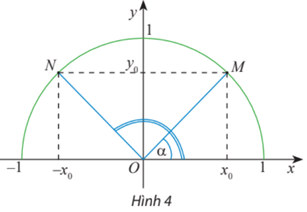
   Trả lời:

   Gọi đường kính của nửa đường tròn đơn vị là AB như hình dưới.
   

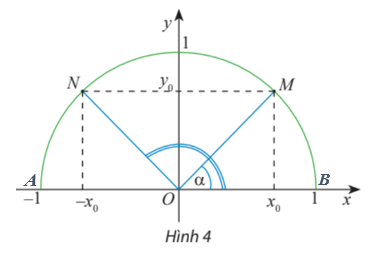
   Do NM // Ox nên hai cung bị chắn giữa dây cung NM và đường kính AB bằng nhau, tức là $\stackrel{⏜}{AN}=\stackrel{⏜}{MB}$
   ⇒ $\widehat{NOA}=\widehat{xOM}=\alpha$  (hai góc ở tâm bằng nhau).
   Mặt khác  $\widehat{xON}$+ $\widehat{NOA}$  = 180° (hai góc kề bù).
   ⇒ $\widehat{xON}$  + $\widehat{xOM}$  = 180°.
   Vậy $\widehat{xON}$  + $\widehat{xOM}$  = 180°.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tính các giá trị lượng giác: sin120°; cos150°; cot135°.
   
   

   Câu hỏi:
   

   Tính các giá trị lượng giác: sin120°; cos150°; cot135°.

   Trả lời:

   Ta có sin120° = sin(180° – 60°) = sin60° = $\frac{\sqrt{3}}{2}$ ;
   cos150° = cos(180° – 30°) = – cos30° = $-\frac{\sqrt{3}}{2}$  ;
   cot135° = cot(180° – 45°) = – cot45° = –1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====