Cho hình thang ABCD có hai đáy là AB và DC (Hình 15). Điểm M nằm trên đoạn DC. a) Gọi tên các vectơ cùng hướng với vectơ AB→. b) Gọi tên các vectơ ngược hướng với vectơ DM→.

Câu hỏi:

Cho hình thang ABCD có hai đáy là AB và DC (Hình 15). Điểm M nằm trên đoạn DC.

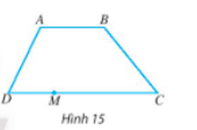
a) Gọi tên các vectơ cùng hướng với vectơ $\overrightarrow{AB}$.
b) Gọi tên các vectơ ngược hướng với vectơ $\overrightarrow{DM}$.

Trả lời:

Do ABCD là hình thang có hai đáy là AB và DC nên AB // DC.
Lại có M nằm trên đoạn DC nên DM // AB, MC // AB.
a) Các vectơ $\overrightarrow{DM},\overrightarrow{MC},\overrightarrow{DC}$ đều có giá song song với giá của vectơ $\overrightarrow{AB}$ nên chúng cùng phương, hơn nữa chúng đều có hướng đi từ trái qua phải.
Do đó các vectơ cùng hướng với vectơ $\overrightarrow{AB}$ là: $\overrightarrow{DM},\overrightarrow{MC},\overrightarrow{DC}$.
b) Vectơ $\overrightarrow{DM}$ và $\overrightarrow{BA}$ có giá song song với nhau nên chúng cùng phương, mà chúng có hướng ngược nhau nên hai vectơ này ngược hướng.
Các vectơ $\overrightarrow{CM},\overrightarrow{CD}$, $\overrightarrow{MD}$ có giá trùng với giá của vectơ $\overrightarrow{DM}$ (đều là đường thẳng DC) nên chúng cùng phương.
Lại có các vectơ $\overrightarrow{CM},\overrightarrow{CD}$, $\overrightarrow{MD}$ có hướng ngược với vectơ $\overrightarrow{DM}$.
Do đó các vectơ ngược hướng với vectơ $\overrightarrow{DM}$ là: $\overrightarrow{CM},\overrightarrow{CD}$, $\overrightarrow{MD}$ và $\overrightarrow{BA}$.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

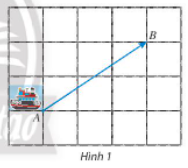
1. Trong thông báo: Có một con tàu chở 500 tấn hàng từ cảng A đến cảng B cách nhau 500 km. Bạn hãy tìm sự khác biệt giữa hai đại lượng sau: – Khối lượng của hàng: 500 tấn. – Độ dịch chuyển của tàu: 500 km từ A đến B.
   
   

   Câu hỏi:
   

   Trong thông báo: Có một con tàu chở 500 tấn hàng từ cảng A đến cảng B cách nhau 500 km.
   Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:
   – Khối lượng của hàng: 500 tấn.
   – Độ dịch chuyển của tàu: 500 km từ A đến B.
   

   Trả lời:

   Sự khác biệt giữa hai đại lượng đã cho là:
   – Khối lượng của hàng là đại lượng chỉ có độ lớn vì hàng trên tàu có khối lượng 500 tấn. Ta gọi đại lượng dạng này là đại lượng vô hướng.
   – Độ dịch chuyển của tàu là đại lượng bao gồm cả độ lớn và hướng vì con tàu có độ dịch chuyển dài 500 km theo hướng từ A đến B.
   Ta gọi đại lượng dạng này là đại lượng có hướng.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
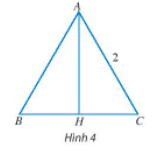
2. Tìm điểm đầu, điểm cuối, giá và độ dài của các vectơ CH→,  CB→,  HA→ trong Ví dụ 1.
   
   

   Câu hỏi:
   

   Tìm điểm đầu, điểm cuối, giá và độ dài của các vectơ $\overrightarrow{CH},\overrightarrow{CB},\overrightarrow{HA}$ trong Ví dụ 1.
   

   Trả lời:

   Vectơ $\overrightarrow{CH}$ có điểm đầu là C, điểm cuối là H và có giá là đường thẳng CH (hay chính là đường thẳng BC).
   Vectơ $\overrightarrow{CB}$ có điểm đầu là C, điểm cuối là B và có giá là đường thẳng BC.
   Vectơ $\overrightarrow{HA}$ có điểm đầu là H, điểm cuối là A và có giá là đường thẳng AH.
   Do H là trung điểm của BC nên CH = $\frac{1}{2}BC$= $\frac{1}{2}.2=1$.
   Theo Ví dụ 1, ta có AH = $\sqrt{3}$.
   Suy ra $\left|\overrightarrow{CH}\right|=CH=1,\left|\overrightarrow{CB}\right|=CB=2,\left|\overrightarrow{HA}\right|=HA=AH=\sqrt{3}$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
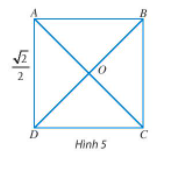
3. Cho hình vuông ABCD có cạnh bằng 22, hai đường chéo cắt nhau tại O (Hình 5). Tìm độ dài của các vectơ  AC→, BD→, OA→, AO→.
   
   

   Câu hỏi:
   

   Cho hình vuông ABCD có cạnh bằng $\frac{\sqrt{2}}{2}$, hai đường chéo cắt nhau tại O (Hình 5). Tìm độ dài của các vectơ  $\overrightarrow{AC},\overrightarrow{BD},\overrightarrow{OA},\overrightarrow{AO}$.
   

   Trả lời:

   Do ABCD là hình vuông nên góc ADC là góc vuông.
   Xét tam giác ADC vuông tại D, theo định lí Pythagore ta có:
   AC² = AD² + DC²₂²
   Suy ra $AC=\sqrt{A{D}^2+D{C}^2}=\sqrt{{\left(\frac{\sqrt{2}}{2}\right)}^2+{\left(\frac{\sqrt{2}}{2}\right)}^2}=1$.
   Do ABCD là hình vuông nên hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm của mỗi đường.
   Nên AC = BD và O là trung điểm của AC và BD.
   Khi đó: BD = AC = 1 và OA = AO = $\frac{1}{2}AC$ = $\frac{1}{2}.1=\frac{1}{2}$.
   Suy ra: $\left|\overrightarrow{AC}\right|=1,\left|\overrightarrow{BD}\right|=1,\left|\overrightarrow{OA}\right|=\frac{1}{2},\left|\overrightarrow{AO}\right|=\frac{1}{2}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
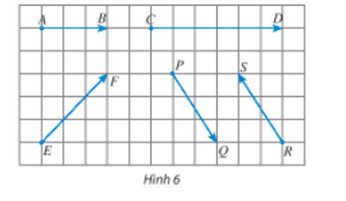
4. Bạn có nhận xét gì về giá của các cặp vectơ AB→ và CD→, PQ→ và RS→ trong Hình 6?  
   
   

   Câu hỏi:
   

   Bạn có nhận xét gì về giá của các cặp vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$, $\overrightarrow{PQ}$ và $\overrightarrow{RS}$ trong Hình 6?
   
    

   Trả lời:

   + Giá của vectơ $\overrightarrow{AB}$ là đường thẳng AB, giá của vectơ $\overrightarrow{CD}$ là đường thẳng CD.
   Quan sát Hình 6 ta thấy hai đường thẳng AB, CD là trùng nhau.
   Do đó giá của hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$ là trùng nhau.
   + Giá của vectơ $\overrightarrow{PQ}$ là đường thẳng PQ, giá của vectơ $\overrightarrow{RS}$ là đường thẳng RS.
   Quan sát Hình 6 ta thất hai đường thẳng PQ và RS song song với nhau.
   Do đó giá của hai vectơ $\overrightarrow{PQ}$ và $\overrightarrow{RS}$ là song song với nhau.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
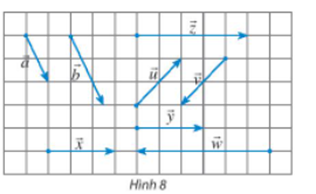
5. Quan sát Hình 8 và gọi tên các vectơ: a) Cùng phương với vectơ x→; b) Cùng hướng với vectơ a→; c) Ngược hướng với vectơ u→.
   
   

   Câu hỏi:
   

   Quan sát Hình 8 và gọi tên các vectơ:
   a) Cùng phương với vectơ $\overrightarrow{x}$;
   b) Cùng hướng với vectơ $\overrightarrow{a}$;
   c) Ngược hướng với vectơ $\overrightarrow{u}$.
   

   Trả lời:

   Quan sát Hình 8 ta thấy:
   a) Vectơ $\overrightarrow{\text{w}}$ có giá trùng với giá của vectơ $\overrightarrow{x}$, vectơ $\overrightarrow{y}$ có giá song song với giá của vectơ $\overrightarrow{x}$, vectơ $\overrightarrow{z}$ có giá song song với giá của vectơ $\overrightarrow{x}$.
   Vậy các vectơ cùng phương với vectơ $\overrightarrow{x}$ là vectơ $\overrightarrow{y},\overrightarrow{\text{w}},\overrightarrow{z}$.
   b) Hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ có giá song song với nhau nên chúng cùng phương.
   Lại có hai vectơ này có cùng hướng đi từ trên chéo xuống dưới.
   Vậy vectơ cùng hướng với vectơ $\overrightarrow{a}$ là vectơ $\overrightarrow{b}$.
   c) Hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ có giá song song với nhau nên chúng cùng phương.
   Lại có hai vectơ này có hướng ngược nhau.
   Vậy vectơ ngược hướng với vectơ $\overrightarrow{u}$ là vectơ $\overrightarrow{v}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====