Câu hỏi:
Một lớp học có 16 học sinh học giỏi môn Toán; 12 học sinh học giỏi môn Văn; 8 học sinh vừa học giỏi môn Toán và Văn; 19 học sinh không học giỏi cả hai môn Toán và Văn. Hỏi lớp học có bao nhiêu học sinh?
A. 31;
B. 54;
C. 39;
Đáp án chính xác
D. 47.
Trả lời:
Đáp án đúng là: C
Gọi A là tập hợp gồm các học sinh trong lớp; B là tập số học sinh giỏi Toán; C là tập số học sinh giỏi Văn; D là tập số học sinh không giỏi cả 2 môn Toán và Văn.
Khi đó n(B) = 16, n(C) = 12, n(B∩C) = 8, n(D) = 19.
Số học sinh trong lớp giỏi ít nhất một trong hai môn Toán hoặc Văn là:
n(B∪C) = n(B) + n(C) – n(B∩C) = 16 + 12 – 8 = 20.
Ta có A = \((B \cup C) \cup D\)
Số học sinh trong lớp là: n(A) = n(B∪C) + n(D) = 20 + 19 = 39 (học sinh).
Được thể hiện trong biểu đồ Ven như sau:
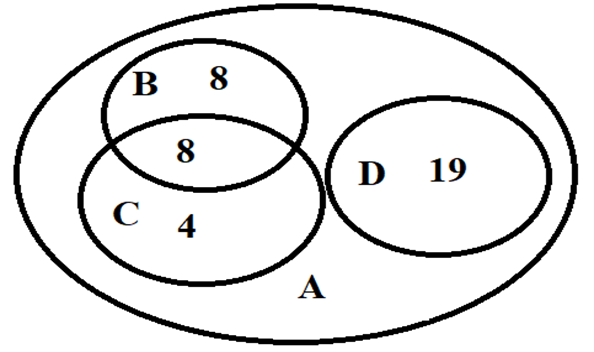
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số tập con của tập A = {1; 2; 3} là
Câu hỏi:
Số tập con của tập A = {1; 2; 3} là
A. 8;
Đáp án chính xác
B. 6;
C. 5;
D. 7.
Trả lời:
Đáp án đúng là: A
Các tập con gồm {1}; {2}; {3}; {1; 2}; {1;3}; {2; 3}; {1; 2; 3}; \(\emptyset \).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hãy liệt kê các phần tử của tập hợp \(X = \,{\rm{\{ }}x \in \mathbb{R},\,{x^2} + x + 1 = 0\} \)
Câu hỏi:
Hãy liệt kê các phần tử của tập hợp \(X = \,{\rm{\{ }}x \in \mathbb{R},\,{x^2} + x + 1 = 0\} \)
A. X = \(\emptyset \);
Đáp án chính xác
B. X = {0};
C. X = 0;
D. X = {\(\emptyset \)}.
Trả lời:
Đáp án đúng là: A
Phương trình x2 + x + 1 = 0 vô nghiệm nên tập X không có phần tử nào.
Vậy tập X = \(\emptyset \).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số tập con có 2 phần tử của tập M = {1; 2; 3; 4; 5; 6}
Câu hỏi:
Số tập con có 2 phần tử của tập M = {1; 2; 3; 4; 5; 6}
A. 15;
Đáp án chính xác
B. 16;
C. 18;
D. 22.
Trả lời:
Đáp án đúng là: A
Tập con có 2 phần tử của tập M gồm: {1; 2}; {1; 3}; {1; 4}; {1; 5}; {1;6}; {2; 3}; {2; 4}; {2; 5}; {2; 6}; {3; 4}; {3; 5}; {3; 6}; {4; 5}; {4; 6}; {5; 6}.
Vậy tập M có 15 tập con có 2 phần tử.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hai tập hợp A = {0; 2; 3; 5} và B = {2; 7}. Khi đó \({\rm{A}} \cap {\rm{B}}\)
Câu hỏi:
Cho hai tập hợp A = {0; 2; 3; 5} và B = {2; 7}. Khi đó \({\rm{A}} \cap {\rm{B}}\)
A. {2; 5};
B. {2};
Đáp án chính xác
C. \(\emptyset \);
D. {0; 2; 3; 5; 7}.
Trả lời:
Đáp án đúng là: B
Vì phần tử 2 vừa thuộc A vừa thuộc B nên \({\rm{A}} \cap {\rm{B}} = \left\{ 2 \right\}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho A = {0; 1; 2; 3; 4}; B = {2; 3; 4; 5; 6}. Tìm tập \(\left( {{\rm{A}}\backslash {\rm{B}}} \right) \cup \left( {{\rm{B}}\backslash {\rm{A}}} \right)\)
Câu hỏi:
Cho A = {0; 1; 2; 3; 4}; B = {2; 3; 4; 5; 6}. Tìm tập \(\left( {{\rm{A}}\backslash {\rm{B}}} \right) \cup \left( {{\rm{B}}\backslash {\rm{A}}} \right)\)
A. {5; 6};
B. {1; 2};
C. {2; 3; 4};
D. {0; 1; 5; 6}.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
Ta có tập hợp A\B là tập các phần tử thuộc tập A nhưng không thuộc tập B nên \(\left( {{\rm{A}}\backslash {\rm{B}}} \right) = {\rm{\{ 0;}}\,{\rm{1\} }}\).
Tập hợp B\A là tập các phần tử thuộc tập B nhưng không thuộc tập A nên \(\left( {{\rm{B}}\backslash {\rm{A}}} \right) = {\rm{\{ }}5;\,6\} \).
\( \Rightarrow \left( {{\rm{A}}\backslash {\rm{B}}} \right) \cup \left( {{\rm{B}}\backslash {\rm{A}}} \right) = \left\{ {0;\,1;\,5;\,6} \right\}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====