Một công ty dự định sản xuất hai loại sản phẩm I và II. Các sản phẩm này được chế tạo từ hai loại nguyên liệu A, B. Số kilôgam dự trữ từng loại nguyên liệu và số kilôgam từng loại cần dùng để sản xuất 1 kg sản phẩm được cho trong bảng sau : Loại nguyên liệu Số kilôgam nguyên liệu dự trữ Số kilôgam nguyên liệu cần dùng sản xuất 1 kg sản phẩm I II A 8 2 1 B 12 2 2 Công ty đó nên sản xuất bao nhiêu sản phẩm mỗi loại để tiền lãi thu về lớn nhất ? Biết rằng, mỗi kilogam sản phẩm loại I lãi 10 triệu đồng, mỗi sản phẩm loại II lãi 20 triệu đồng.

By 0

Câu hỏi:

Một công ty dự định sản xuất hai loại sản phẩm I và II. Các sản phẩm này được chế tạo từ hai loại nguyên liệu A, B. Số kilôgam dự trữ từng loại nguyên liệu và số kilôgam từng loại cần dùng để sản xuất 1 kg sản phẩm được cho trong bảng sau :

Loại nguyên liệu

Số kilôgam nguyên liệu dự trữ

Số kilôgam nguyên liệu cần dùng sản xuất 1 kg sản phẩm

I

II

A

8

2

1

B

12

2

2

Công ty đó nên sản xuất bao nhiêu sản phẩm mỗi loại để tiền lãi thu về lớn nhất ? Biết rằng, mỗi kilogam sản phẩm loại I lãi 10 triệu đồng, mỗi sản phẩm loại II lãi 20 triệu đồng.

A. 5 kg loại I và 1 kg loại II;

B. 5 kg loại I và 5 kg loại II;

C. 6 kg loại I và 0 kg loại II;

D. 0 kg loại I và 6 kg loại II;

Đáp án chính xác

Trả lời:

Đáp án đúng là: D
Gọi x (kg) là khối lượng sản phẩm I, y (kg) là khối lượng sản phẩm II mà công ty sản xuất. Hiển nhiên x ≥ 0 và y ≥ 0.
Số nguyên liệu A cần dùng để sản xuất ra x kg sản phẩm I là 2x (kg).
Số nguyên liệu A cần dùng để sản xuất ra y kg sản phẩm II là y (kg).
Tổng nguyên liệu loại I cần dùng là 2x + y (kg).
Mặt khác, số nguyên liệu dự trữ loại I là 8 kg, nên ta có bất phương trình : 2x + y ≤ 8.
Tương tự, số nguyên liệu B cần dùng để sản xuất ra x kg sản phẩm I là 2x (kg).
Số nguyên liệu B cần dùng để sản xuất ra y kg sản phẩm II là 2y (kg).
Tổng nguyên liệu loại II cần dùng là 2x + 2y (kg).
Số nguyên liệu dự trữ loại II là 12 kg, nên ta có bất phương trình : 2x + 2y ≤ 12, tức là x + y ≤ 6.
Vậy ta có hệ bất phương trình sau :
\(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{2x{\rm{ }} + {\rm{ }}y \le 8}\\{x{\rm{ }} + {\rm{ }}y \le 6}\end{array}} \right.\)
Biểu diễn miền nghiệm của hệ này trên mặt phẳng tọa độ Oxy ta được hình sau :
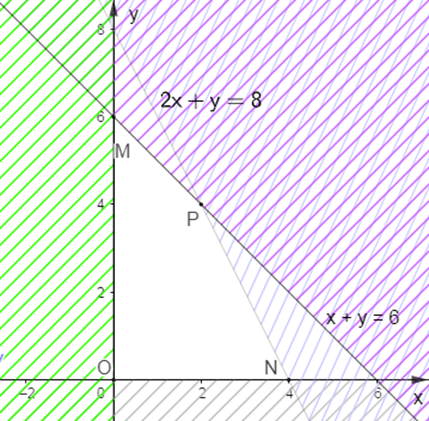
Một công ty dự định sản xuất hai loại sản phẩm I và II. Các sản phẩm này (ảnh 1)

Miền nghiệm của hệ là miền tứ giác OMPN (bao gồm các cạnh) với các đỉnh O(0 ; 0) ; M (0 ; 6) ; P(2 ; 4) ; N(4 ; 0).
Gọi F là số tiền lãi thu được (đơn vị : triệu đồng) , ta có :
Tiền lãi thu được từ x kg sản phẩm loại I là : 10x (triệu đồng) .
Tiền lãi thu được từ y kg sản phẩm loại II là : 20y (triệu đồng).
Khi đó F = 10x + 20y
Tính giá trị của F tại các đỉnh của tứ giác OMPN:
Tại O (0 ; 0) : F = 10.0 +20.0 = 0 ;
Tại M(0 ; 6) : F = 10 . 0 + 20 . 6 = 120 ;
Tại P(2 ; 4) : F = 10 . 2 + 20 . 4= 90;
Tại N(4 ; 0): F = 10 . 4 + 20 . 0 = 40.
F đạt lớn nhất bằng 120 tại M(0 ; 6).
Vậy công ty nên sản xuất 0 kg sản phẩm loại I và 6 kg sản phẩm loại II để thu về tiền lãi lớn nhất.
Ta chọn đáp án D.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

  1. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn ?

    Câu hỏi:

    Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn ?

    A. \(\left\{ \begin{array}{l}x + 3y \ge 0\\2x \le 0\end{array} \right.\)

    Đáp án chính xác

    B. \(\left\{ \begin{array}{l}{x^2} + 3y \ge 2\\2x + y \le – 1\end{array} \right.\)

    C. \(\left\{ \begin{array}{l}4x + 3y – 1 \ge 0\\x + {y^3} > 0\end{array} \right.\)

    D. \(\left\{ \begin{array}{l} – {x^2} + 3y \ge 5\\x + {y^3} \le 1\end{array} \right.\)

    Trả lời:

    Đáp án đúng là: ACác hệ bất phương trình \(\left\{ \begin{array}{l}{x^2} + 3y \ge 2\\2x + y \le – 1\end{array} \right.\); \(\left\{ \begin{array}{l}4x + 3y – 1 \ge 0\\x + {y^3} > 0\end{array} \right.\); \(\left\{ \begin{array}{l} – {x^2} + 3y \ge 5\\x + {y^3} \le 1\end{array} \right.\) đều chứa các bất phương trình bậc hai hoặc bậc ba như : x2 + 3y ≥ 2 ; x + y3 > 0 ; – x2 + 3y ≥ 5.Do đó, các hệ bất phương trình \(\left\{ \begin{array}{l}{x^2} + 3y \ge 2\\2x + y \le – 1\end{array} \right.\); \(\left\{ \begin{array}{l}4x + 3y – 1 \ge 0\\x + {y^3} > 0\end{array} \right.\); \(\left\{ \begin{array}{l} – {x^2} + 3y \ge 5\\x + {y^3} \le 1\end{array} \right.\) không phải là hệ bất phương trình bậc nhất hai ẩn.Hệ \(\left\{ \begin{array}{l}x + 3y \ge 0\\2x \le 0\end{array} \right.\) có hai bất phương trình x + 3y ≥ 0 và 2x ≤ 0 đều là các bất phương trình bậc nhất hai ẩn.Vậy ta chọn đáp án A.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  2. Trong các khẳng định sau, khẳng định nào đúng?

    Câu hỏi:

    Trong các khẳng định sau, khẳng định nào đúng?

    A. Điểm O(0 ; 0) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – x + 3y \ge 0\\2x \le 0\end{array} \right.\)

    Đáp án chính xác

    B. Điểm M(1 ; 0) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – x + 3y \ge 0\\2x \le 0\end{array} \right.\)

    C. Điểm N(0 ; –1) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – x + 3y \ge 0\\2x \le 0\end{array} \right.\)

    D. Điểm P(1 ; 1) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – x + 3y \ge 0\\2x \le 0\end{array} \right.\).

    Trả lời:

    Đáp án đúng là: A+ Vì –0 + 3.0 = 0 và 2.0 = 0 nên cặp số (0; 0) là nghiệm của cả hai bất phương trình –x + 3y ≥ 0 và 2x ≤ 0.Suy ra điểm O(0; 0) thuộc miền nghiệm của hệ \(\left\{ \begin{array}{l} – x + 3y \ge 0\\2x \le 0\end{array} \right.\). Vậy khẳng định A là đúng.+ Vì –1 + 3.0 = –1 < 0 và 2. (–1) = –2 < 0 nên cặp số (1 ; 0) không là nghiệm của bất phương trình –x + 3y ≥ 0.Suy ra điểm M(1 ; 0) không thuộc miền nghiệm của hệ \(\left\{ \begin{array}{l} – x + 3y \ge 0\\2x \le 0\end{array} \right.\). Vậy khẳng định B là sai.+ Vì –0 + 3. (–1) = –3 < 0 và 2. 0 = 0 nên cặp số (0; –1) không là nghiệm của bất phương trình –x + 3y ≥ 0.Suy ra điểm N(0 ; –1) không thuộc miền nghiệm của hệ \(\left\{ \begin{array}{l} – x + 3y \ge 0\\2x \le 0\end{array} \right.\). Vậy khẳng định C là sai.+ Vì –1 + 3. 1 = 2 > 0 và 2. 1 = 2 > 0 nên cặp số (1; 1) không là nghiệm của bất phương trình 2x ≤ 0.Suy ra điểm P(1; 1) không thuộc miền nghiệm của hệ \(\left\{ \begin{array}{l} – x + 3y \ge 0\\2x \le 0\end{array} \right.\). Vậy khẳng định D là sai.Vậy ta chọn đáp án A.>>

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  3. Tìm khẳng định sai trong các khẳng định sau:

    Câu hỏi:

    Tìm khẳng định sai trong các khẳng định sau:

    A. Hệ \(\left\{ \begin{array}{l}x + y \ge – 1\\{y^2} – 1 \le 0\end{array} \right.\) không phải là hệ bất phương trình bậc nhất hai ẩn;

    B. Hệ \(\left\{ \begin{array}{l}x \ge 1 + y\\5x + y < 0\end{array} \right.\) là hệ bất phương trình bậc nhất hai ẩn;>

    C. Hệ \(\left\{ \begin{array}{l}x + 1 + y > 0\\{x^2} + y < 0\end{array} \right.\) là hệ bất phương trình bậc nhất hai ẩn;>

    Đáp án chính xác

    D. Hệ \(\left\{ \begin{array}{l}\frac{1}{2}x + 2y < 7\\x + 3y \le 0\end{array} \right.\) là hệ bất phương trình bậc nhất hai ẩn;>

    Trả lời:

    Đáp án đúng là: C+ Vì \(\left\{ \begin{array}{l}x + y \ge – 1\\{y^2} – 1 \le 0\end{array} \right.\) chứa bất phương trình bậc hai y2 – 1 ≤ 0 nên hệ này không phải là hệ bất phương trình bậc nhất hai ẩn.Do đó khẳng định A đúng.+ Vì \(\left\{ \begin{array}{l}x \ge 1 + y\\5x + y < 0\end{array} \right.\) chứa hai bất phương trình x ≥ 1 + y và 5x + y < 0 đều là các bất phương trình bậc nhất hai ẩn, nên hệ này là hệ bất phương trình bậc nhất hai ẩn.Do đó khẳng định B đúng.+ Vì \(\left\{ \begin{array}{l}x + 1 + y > 0\\{x^2} + y < 0\end{array} \right.\) chứa bất phương trình bậc hai x2>> + y < 0 nên hệ này không phải là hệ bất phương trình bậc nhất hai ẩn.Do đó khẳng định C sai.+ Vì \(\left\{ \begin{array}{l}\frac{1}{2}x + 2y < 7\\x + 3y \le 0\end{array} \right.\)chứa hai bất phương trình \(\frac{1}{2}x + y < 7\) và x + 3y ≤ 0 đều là các bất phương trình bậc nhất hai ẩn nên hệ này là hệ bất phương trình bậc nhất hai ẩn.Do đó khẳng định D đúng.Vậy ta chọn đáp án C.>>

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  4. Cho hệ bất phương trình \(\left\{ \begin{array}{l} – x + 2y \ge 2\\2x + y \le – 1\end{array} \right.\). Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?

    Câu hỏi:

    Cho hệ bất phương trình \(\left\{ \begin{array}{l} – x + 2y \ge 2\\2x + y \le – 1\end{array} \right.\). Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?

    A. M(0; 1);         

    B. N(–1; 1);        

    Đáp án chính xác

    . P(–1; 4);           

    D. Q(1; 3).

    Trả lời:

    Đáp án đúng là: B
    + Ta có : –0 + 2.1 = 2 và 2.0 + 1 = 1 > –1.
    Do đó cặp số (0; 1) không là nghiệm của bất phương trình 2x + y ≤ –1.
    Vậy nên cặp số (0; 1) không là nghiệm của hệ bất phương trình\(\left\{ \begin{array}{l} – x + 2y \ge 2\\2x + y \le – 1\end{array} \right.\).
    Suy ra điểm M(0; 1) không thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – x + 2y \ge 2\\2x + y \le – 1\end{array} \right.\)
    + Ta có : –(–1) +2.1 = 3 > 2 và 2.(–1) + 1 = –1.
    Do đó cặp số (–1; 1) là nghiệm của cả hai bất phương trình –x + 3y ≥2 và 2x + y ≤ –1.
    Vậy nên, cặp số (–1; 1) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – x + 2y \ge 2\\2x + y \le – 1\end{array} \right.\).
    Suy ra điểm N(–1; 1) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – x + 2y \ge 2\\2x + y \le – 1\end{array} \right.\).
    + Ta có : –(–1) + 2.4 = 9 > 2 và 2.(–1) + 4 = 2 > –1.
    Do đó cặp số (–1; 4) không là nghiệm của bất phương trình 2x + y ≤ –1.
    Vậy nên cặp số (–1; 4) không là nghiệm của hệ bất phương trình\(\left\{ \begin{array}{l} – x + 2y \ge 2\\2x + y \le – 1\end{array} \right.\).
    Suy ra điểm P(–1; 4) không thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – x + 2y \ge 2\\2x + y \le – 1\end{array} \right.\)
    + Ta có : –1 + 2.3 = 5 > 2 và 2.1 + 3 = 5 > –1.
    Do đó cặp số (1; 3) không là nghiệm của bất phương trình 2x + y ≤ –1.
    Vậy nên cặp số (1; 3) không là nghiệm của hệ bất phương trình\(\left\{ \begin{array}{l} – x + 2y \ge 2\\2x + y \le – 1\end{array} \right.\).
    Suy ra điểm Q(1; 3) không thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – x + 2y \ge 2\\2x + y \le – 1\end{array} \right.\)
    Vậy điểm N(–1; 1) thuộc miền nghiệm của hệ bất phương trình đã cho nên ta chọn đáp án B.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  5. Cho hệ bất phương trình \(\left\{ \begin{array}{l} – 3x + y > – 2\\x + 2y \le 1\end{array} \right.\). Và các điểm sau: M(–1 ; 2), N(0; –1), O(0; 0). Có mấy điểm thuộc miền nghiệm của hệ bất phương trình đã cho?

    Câu hỏi:

    Cho hệ bất phương trình \(\left\{ \begin{array}{l} – 3x + y > – 2\\x + 2y \le 1\end{array} \right.\). Và các điểm sau: M(–1 ; 2), N(0; –1), O(0; 0). Có mấy điểm thuộc miền nghiệm của hệ bất phương trình đã cho?

    A. 0;

    B. 1;  

    C. 2;

    Đáp án chính xác

    D. 3.

    Trả lời:

    Đáp án đúng là: C
    + Ta có : –3. (–1)  + 2 = 5 > –2 và –1 + 2.2 = 3 > 1.
    Do đó cặp số (–1 ; 2) không là nghiệm của bất phương trình x + 2y ≤ 1.
    Vậy nên cặp số (–1 ; 2) không là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – 3x + y > – 2\\x + 2y \le 1\end{array} \right.\).
    Suy ra điểm M(–1 ; 2) không thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – 3x + y > – 2\\x + 2y \le 1\end{array} \right.\).
    + Ta có : –3. 0 + (–1)= –1 > –2 và 0 + 2. (–1) = –2 < 1.
    Do đó cặp số (0; –1) là nghiệm của cả hai bất phương trình –3x + y > –2 và x + 2y ≤ 1.
    Vậy nên cặp số (0; –1) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – 3x + y > – 2\\x + 2y \le 1\end{array} \right.\).
    Suy ra điểm M(0; –1)  thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – 3x + y > – 2\\x + 2y \le 1\end{array} \right.\).
    + Ta có : –3. 0  + 0 = 0 > –2 và 0 + 2.0 = 0 < 1.
    Do đó cặp số (0 ; 0) là nghiệm của cả hai bất phương trình –3x + y > –2 và x + 2y ≤ 1.
    Vậy nên cặp số (0 ; 0) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – 3x + y > – 2\\x + 2y \le 1\end{array} \right.\).
    Suy ra điểm O(0 ; 0) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} – 3x + y > – 2\\x + 2y \le 1\end{array} \right.\).
    Vậy hai điểm M(0; –1)  và O(0 ; 0) thuộc miền nghiệm của hệ \(\left\{ \begin{array}{l} – 3x + y > – 2\\x + 2y \le 1\end{array} \right.\).
    Do đó ta chọn đáp án C.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

Bài liên quan:

Leave a Comment

Back to Top
Menu