b) Nếu ABCD là hình chữ nhật thì SA→2+SC→2=SB→2+SD→2

Câu hỏi:

b) Nếu ABCD là hình chữ nhật thì ${\overrightarrow{SA}}^2+{\overrightarrow{SC}}^2={\overrightarrow{SB}}^2+{\overrightarrow{SD}}^2$

Trả lời:

b) Ta có ${\overrightarrow{SA}}^2={\left(\overrightarrow{SO}+\overrightarrow{OA}\right)}^2={\overrightarrow{SO}}^2+{\overrightarrow{OA}}^2+2\overrightarrow{SO}.\overrightarrow{OA}$ ,
${\overrightarrow{SC}}^2={\left(\overrightarrow{SO}+\overrightarrow{OC}\right)}^2={\overrightarrow{SO}}^2+{\overrightarrow{OC}}^2+2\overrightarrow{SO}.\overrightarrow{OC}$
Suy ra ${\overrightarrow{SA}}^2+{\overrightarrow{SC}}^2=2{\overrightarrow{SO}}^2+{\overrightarrow{OA}}^2+{\overrightarrow{OC}}^2+2\overrightarrow{SO}\left(\overrightarrow{OA}+\overrightarrow{OC}\right)$
$=2\left({\overrightarrow{SO}}^2+{\overrightarrow{OA}}^2\right)$(vì $\overrightarrow{OA}$  và $\overrightarrow{OC}$  là hai vectơ đối nhau nên $\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}$)
$=2\left(S{O}^2+O{A}^2\right)$

Tương tự ${\overrightarrow{SB}}^2+{\overrightarrow{SD}}^2=2\left(S{O}^2+O{B}^2\right)$
Mà ABCD là hình chữ nhật nên OA = OB
Suy ra ${\overrightarrow{SA}}^2+{\overrightarrow{SC}}^2={\overrightarrow{SB}}^2+{\overrightarrow{SD}}^2$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng AC→+BD→=AD→+BC→=2MN→
   
   

   Câu hỏi:
   

   Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng $\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{BC}=2\overrightarrow{MN}$

   Trả lời:

   
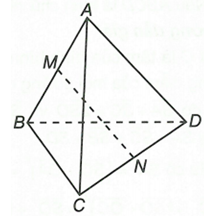
   Ta có $\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{BC}$
   $\iff \overrightarrow{AC}-\overrightarrow{AD}=\overrightarrow{BC}-\overrightarrow{BD}$

   $\iff \overrightarrow{DC}=\overrightarrow{DC}$(đẳng thức này đúng).
   Do M, N lần lượt là trung điểm các cạnh AB và CD
   nên $\left\{\begin{array}{l}\overrightarrow{AM}+\overrightarrow{BM}=0\\ \overrightarrow{NC}+\overrightarrow{ND}=0\end{array}\right.$
   Do đó $\overrightarrow{AD}+\overrightarrow{BC}=\left(\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NB}\right)+\left(\overrightarrow{BM}+\overrightarrow{MN}+\overrightarrow{ND}\right)$
   $=\left(\overrightarrow{AM}+\overrightarrow{BM}\right)+\left(\overrightarrow{NB}+\overrightarrow{ND}\right)+2\overrightarrow{MN}=2\overrightarrow{MN}$

   Vậy $\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{BC}=2\overrightarrow{MN}$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình hộp ABCD.A’B’C’D’. Sử dụng các đỉnh của hình hộp làm điểm đầu và điểm cuối của vectơ. a) Hãy kể tên các vectơ bằng nhau lần lượt bằng các vectơ AB→,AC→,AD→,AA’→
   
   

   Câu hỏi:
   

   Cho hình hộp ABCD.A’B’C’D’. Sử dụng các đỉnh của hình hộp làm điểm đầu và điểm cuối của vectơ.
   a) Hãy kể tên các vectơ bằng nhau lần lượt bằng các vectơ $\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD},\overrightarrow{A{A}^{‘}}$

   Trả lời:

   a) Ta có
   
   +) $\overrightarrow{AB}=\overrightarrow{DC}=\overrightarrow{A^{‘}{B}^{‘}}=\overrightarrow{D^{‘}{C}^{‘}}$

   +) $\overrightarrow{AC}=\overrightarrow{A^{‘}{C}^{‘}}$
   +) $\overrightarrow{AD}=\overrightarrow{BC}=\overrightarrow{A^{‘}{D}^{‘}}=\overrightarrow{B^{‘}{C}^{‘}}$
   +) $\overrightarrow{A{A}^{‘}}=\overrightarrow{B{B}^{‘}}=\overrightarrow{C{C}^{‘}}=\overrightarrow{D{D}^{‘}}$

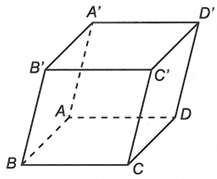
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Hãy kể tên các vectơ luôn có độ dài bằng nhau và bằng độ dài của vectơ BC→ .
   
   

   Câu hỏi:
   

   Hãy kể tên các vectơ luôn có độ dài bằng nhau và bằng độ dài của vectơ $\overrightarrow{BC}$ .

   Trả lời:

   Từ tính chất của hình bình hành, ta suy ra các vectơ luôn có độ dài bằng độ dài của vectơ $\overrightarrow{BC}$ là $\overrightarrow{BC},\overrightarrow{CB},\overrightarrow{AD},\overrightarrow{DA},\overrightarrow{A^{‘}{D}^{‘}},\overrightarrow{D^{‘}{A}^{‘}},\overrightarrow{B^{‘}{C}^{‘}},\overrightarrow{C^{‘}{B}^{‘}}$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. a) Chứng minh SA→+SC→=SB→+SD→
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
   a) Chứng minh $\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}$

   Trả lời:

   
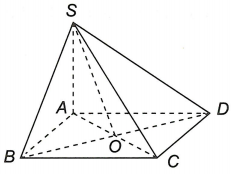
   a) Gọi O là tâm của hình bình hành ABCD thì O là trung điểm của mỗi đường chéo AC và BD.
   Do đó $\overrightarrow{SA}+\overrightarrow{SC}=2\overrightarrow{SO}$  và $\overrightarrow{SB}+\overrightarrow{SD}=2\overrightarrow{SO}$
   Vậy $\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho tứ diện ABCD. Gọi M và N lần lượt là các điểm trên các cạnh AD và BC sao cho AM=2MD,BC=3NC . Chứng minh ba vectơ AB→,CD→,MN→  đồng phẳng.
   
   

   Câu hỏi:
   

   Cho tứ diện ABCD. Gọi M và N lần lượt là các điểm trên các cạnh AD và BC sao cho $AM=2MD,BC=3NC$ . Chứng minh ba vectơ $\overrightarrow{AB},\overrightarrow{CD},\overrightarrow{MN}$  đồng phẳng.

   Trả lời:

   
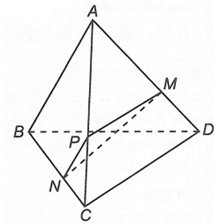
   Ta có $\left\{\begin{array}{l}\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{BN}\\ 2\overrightarrow{MN}=2\left(\overrightarrow{MD}+\overrightarrow{DC}+\overrightarrow{CN}\right)\end{array}\right.$
   Cộng vế theo vế của hai đẳng thức này ta được $3\overrightarrow{MN}=\left(\overrightarrow{MA}+2\overrightarrow{MD}\right)+\left(\overrightarrow{BN}+2\overrightarrow{CN}\right)+\left(\overrightarrow{AB}+2\overrightarrow{DC}\right)$
   Do $\overrightarrow{MA}+2\overrightarrow{MD}=\overrightarrow{0},\overrightarrow{ BN}+2\overrightarrow{CN}=\overrightarrow{0}$ nên $\overrightarrow{MN}=\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{CD}$
   Vậy $\overrightarrow{AB},\overrightarrow{CD},\overrightarrow{MN}$ đồng phẳng.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====