Phương trình của đường thẳng (d) song song với (d’): 6x + 8y – 1 = 0 và cách (d’) một đoạn bằng 2 là:

Câu hỏi:

Phương trình của đường thẳng (d) song song với (d’): 6x + 8y – 1 = 0 và cách (d’) một đoạn bằng 2 là:

A. 6x + 8y + 19 = 0;                  

B. 6x + 8y – 19 = 0; 6x + 8y + 21 = 0;          

C. 6x + 8y + 21 = 0;        

D. 6x + 8y + 19 = 0; 6x + 8y – 21 = 0.

Đáp án chính xác

Trả lời:

Đáp án đúng là: D
(d’) có vectơ pháp tuyến là ${\overrightarrow{n}}^{‘}=(6;8)$
Vì (d) // (d’) nên (d) cũng nhận ${\overrightarrow{n}}^{‘}=(6;8)$  làm vectơ pháp tuyến.
Do đó phương trình (d) có dạng: 6x + 8y + c = 0 (c ≠ –1).
Chọn $A(-\frac{5}{2};2)$  ∈ (d’).
Vì (d) // (d’) nên khoảng cách giữa (d) và (d’) chính là d(A, (d)).
Do đó d(A, (D)) = 2.

⇔ |c + 1| = 20.
⇔ c + 1 = 20 hoặc c + 1 = –20.
⇔ c = 19 (nhận vì 19 ≠ –1) hoặc c = –21 (nhận vì –21 ≠ –1).
Vậy có hai đường thẳng (d) thỏa mãn yêu cầu bài toán có phương trình là:
6x + 8y + 19 = 0 và 6x + 8y – 21 = 0.
Vậy ta chọn phương án D.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Một đường thẳng có bao nhiêu vectơ pháp tuyến?
   
   

   Câu hỏi:
   

   Một đường thẳng có bao nhiêu vectơ pháp tuyến?

   A. 0

   B. 1

   C. 2

   D. Vô số.

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là: D
   Ta có $\overrightarrow{n}$ được gọi là vectơ pháp tuyến của đường thẳng ∆ nếu $\overrightarrow{n}\ne \overrightarrow{0}$và  vuông góc với vectơ chỉ phương của đường thẳng ∆.
   Có vô số vectơ khác $\overrightarrow{0}$và vuông góc với vectơ chỉ phương của đường thẳng ∆.
   Do đó đường thẳng ∆ có vô số vectơ pháp tuyến.
   Vậy ta chọn phương án D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Đường thẳng d có một vectơ chỉ phương là u→=(3;−4). Đường thẳng ∆ vuông góc với d có một vectơ pháp tuyến là:
   
   

   Câu hỏi:
   

   Đường thẳng d có một vectơ chỉ phương là $\overrightarrow{u}=(3;-4)$. Đường thẳng ∆ vuông góc với d có một vectơ pháp tuyến là:

   A. ${\overrightarrow{n}}_1=(4;3)$

   B. ${\overrightarrow{n}}_2=(-4;-3)$

   C. ${\overrightarrow{n}}_3=(3;4)$

   D. ${\overrightarrow{n}}_4=(3;-4)$

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là: D
   

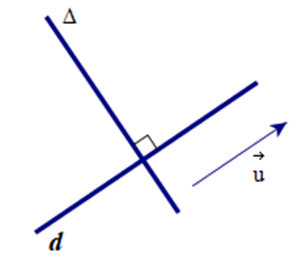
   Vì ∆ ⊥ d nên ∆ nhận vectơ chỉ phương của d là một vectơ pháp tuyến.
   Suy ra ∆ có vectơ pháp tuyến ${\overrightarrow{n}}_{\Delta }=\overrightarrow{u}=(3;-4)$
   Vậy ta chọn phương án

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Vectơ nào sau đây là một vectơ chỉ phương của Δ:{x=5−12ty=−3+3t
   
   

   Câu hỏi:
   

   Vectơ nào sau đây là một vectơ chỉ phương của $\Delta :\{\begin{array}{l}x=5-\frac{1}{2}t\\ y=-3+3t\end{array}$

   A. ${\overrightarrow{u}}_1=(-1;6)$

   Đáp án chính xác

   B. ${\overrightarrow{u}}_2=(\frac{1}{2};3)$

   C. ${\overrightarrow{u}}_3=(5;-3)$

   D. ${\overrightarrow{u}}_4=(-5;3)$

   Trả lời:

   Đáp án đúng là: A
   Đường thẳng ∆ có một vectơ chỉ phương là $\overrightarrow{u}=(-\frac{1}{2};3)$
   Các vectơ chỉ phương còn lại của đường thẳng ∆ sẽ cùng phương với $\overrightarrow{u}$ .
   • Ở phương án A, ta có $\frac{-\frac{1}{2}}{-1}=\frac{3}{6}$  nên ${\overrightarrow{u}}_1$  cùng phương với $\overrightarrow{u}$
   Do đó ${\overrightarrow{u}}_1$  cũng là một vectơ chỉ phương của ∆.
   • Ở phương án B, ta có $\frac{-\frac{1}{2}}{\frac{1}{2}}\ne \frac{3}{6}$nên ${\overrightarrow{u}}_2$  không cùng phương với .
   Do đó ${\overrightarrow{u}}_2$  không là một vectơ chỉ phương của ∆.
   • Tương tự, ta có ${\overrightarrow{u}}_3,{\overrightarrow{u}}_4$  không là vectơ chỉ phương của ∆.
   Vậy ta chọn phương án A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hai điểm A(4; 0), B(0; 5). Phương trình nào sau đây không phải là phương trình của đường thẳng AB?
   
   

   Câu hỏi:
   

   Cho hai điểm A(4; 0), B(0; 5). Phương trình nào sau đây không phải là phương trình của đường thẳng AB?

   A. $y=\frac{-5}{4}x+15$

   Đáp án chính xác

   B. $\frac{x}{4}+\frac{y}{5}=1$

   C. $\frac{x-4}{-4}=\frac{y}{5}$

   D. $\{\begin{array}{l}x=4-4t\\ y=5t\end{array}(t\in ℝ)$

   Trả lời:

   Đáp án đúng là: A
   

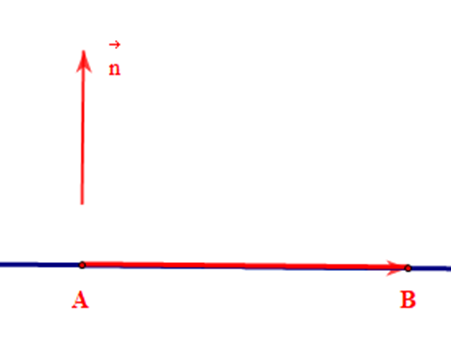
   Với A(4; 0), B(0; 5) ta có: $\overrightarrow{AB}=(-4;5)$
   • Đường thẳng AB là đường thẳng đi qua hai điểm A và B, do đó nhận $\overrightarrow{AB}=(-4;5)$  làm vectơ chỉ phương.
   Khi đó đường thẳng AB nhận $\overrightarrow{n}=(5;4)$  làm vectơ pháp tuyến.
   Đường thẳng AB đi qua điểm A(4; 0), có vectơ pháp tuyến $\overrightarrow{n}=(5;4)$ nên có phương trình tổng quát là: 5(x – 4) + 4(y – 0) = 0
   ⇔ 5x + 4y – 20 = 0 ⇔ 4y = –5x + 20 ⇔ $y=-\frac{5}{4}x+5$
   Do đó phương trình ở phương án A không phải phương trình AB.
   Đến đây ta có thể chọn phương án A.
   • Đường thẳng AB đi qua hai điểm A(4; 0), B(0; 5) nên có phương trình đoạn chắn của là: $\frac{x}{4}+\frac{y}{5}=1$
   Do đó phương án B đúng.
   • Phương trình đường thẳng AB đi qua hai điểm A(4; 0), B(0; 5) là: $\frac{x-4}{0-4}=\frac{y-0}{5-0}\iff \frac{x-5}{-4}=\frac{y}{5}$
   Do đó phương án C đúng.
   • Đường thẳng AB đi qua điểm A(4; 0), có vectơ chỉ phương $\overrightarrow{AB}=(-4;5)$  nên có phương trình tham số là:
   $\{\begin{array}{l}x=4-4t\\ y=5t\end{array}(t\in ℝ)$
   Do đó phương án D đúng.
   Vậy ta chọn phương án A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Giao điểm M của hai đường thẳng (d): {x=1−2ty=−3+5t  và (d’): 3x – 2y – 1 = 0 là:
   
   

   Câu hỏi:
   

   Giao điểm M của hai đường thẳng (d): $\{\begin{array}{l}x=1-2t\\ y=-3+5t\end{array}$  và (d’): 3x – 2y – 1 = 0 là:

   A. $M(0;\frac{1}{2})$

   B. $M(0;-\frac{1}{2})$

   Đáp án chính xác

   C. $M(-\frac{1}{2};0)$

   D. $M(2;-\frac{11}{2})$

   Trả lời:

   Đáp án đúng là: B
   Đường thẳng (d):$\{\begin{array}{l}x=1-2t\\ y=-3+5t\end{array}$
   (d) có vectơ chỉ phương $\overrightarrow{u}=(-2;5)$
   Suy ra (d) có vectơ pháp tuyến $\overrightarrow{n}=(5;2)$
   (d) đi qua A(1; –3), có vectơ pháp tuyến $\overrightarrow{n}=(5;2)$  nên có phương trình tổng quát là:
   5(x – 1) + 2(y + 3) = 0
   ⇔ 5x + 2y + 1 = 0.
   Ta có M là giao điểm của (d) và (d’) nên tọa độ M là nghiệm của hệ phương trình: $\{\begin{array}{l}5x_M+2y_M+1=0\\ 3x_M-2y_M-1=0\end{array}\iff \{\begin{array}{l}{x}_M=0\\ y_M=-\frac{1}{2}\end{array}$

   Khi đó ta có $M(0;-\frac{1}{2})$
   Vậy ta chọn phương án B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====