Trắc nghiệm Toán 7 Bài 1: Hình hộp chữ nhật – Hình lập phương
I. Nhận biết
Câu 1. Có bao nhiêu góc vuông ở đỉnh A của hình hộp chữ nhật ABCD. MNPQ?
A. 1;
B. 2;
C. 3;
D. 4.
Hướng dẫn giải
Đáp án: C
Giải thích:
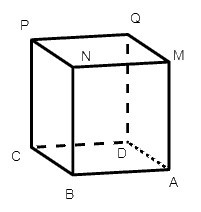
Có 3 góc vuông ở đỉnh A của hình hộp chữ nhật ABCD. MNPQ lần lượt là:
; ; .
Câu 2. Trong các hình hộp dưới đây hình nào là hình lập phương?
A. 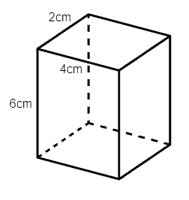
B. 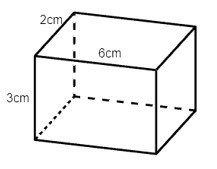
C. 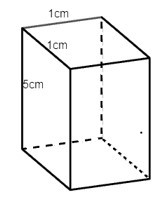
D. 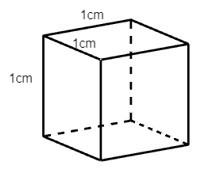
Hướng dẫn giải
Đáp án: D
Giải thích:
Ta thấy hình D là hình hộp có các cạnh bằng nhau nên hình D là hình lập phương.
Câu 3. Mặt nào sau đây không phải là mặt bên của hình hộp chữ nhật ABCD.EFGH?
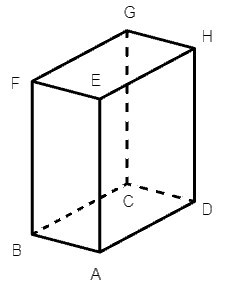
A. ABCD;
B. BFGC;
C. GCDH;
D. BFEA.
Hướng dẫn giải
Đáp án: A
Giải thích:
Hình hộp chữ nhật ABCD.EFGH có 4 mặt bên là: BFEA; EHDA; GCDH; BFGC.
Mặt ABCD là mặt đáy.
Do đó mặt không phải mặt bên của hình chữ nhật là ABCD.
Câu 4. Hãy chọn khẳng định sai.
Hình hộp chữ nhật ABCD.A’B’C’D’ có:
A. 8 đỉnh;
B. 4 mặt bên;
C. 6 cạnh;
D. 6 mặt.
Hướng dẫn giải
Đáp án: C
Giải thích:
Hình hộp chữ nhật này có 12 cạnh: AB; BC; CD; DA; A’B’; C’D’; B’C’; D’A’; AA’; BB’; CC’; DD’.
Do đó phương án C là khẳng định sai.
Câu 5. Số đường chéo của hình hộp chữ nhật ABCD. EFGH:
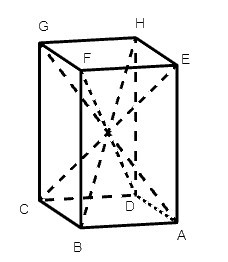
A. 1;
B. 2;
C. 3;
D. 4.
Hướng dẫn giải
Đáp án: D
Giải thích:
Hình hộp chữ nhật ABCD. EFGH có 4 đường chéo lần lượt là: FD, EC, HB, GA.
II. Thông hiểu
Câu 1. Cho hình hộp chữ nhật ABCD. A’B’C’D’. Biết AB = 2 cm. Độ dài cạnh CD và C’D’ là
A. CD = C’D’ = 1 cm;
B. CD = C’D’ = 2 cm;
C. CD = C’D’ = 3 cm;
D. CD = C’D’ = 4 cm.
Hướng dẫn giải
Đáp án: B
Giải thích:
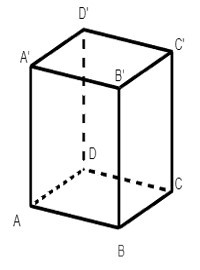
Từ hình hộp chữ nhật ABCD. A’B’C’D’ ta có:
AA’B’B là hình chữ nhật suy ra A’B’ = AB (1)
A’B’C’D’ là hình chữ nhật suy ra C’D’ = A’B’ (2)
ABCD là hình chữ nhật suy ra CD = AB = 2 cm.
Từ (1) và (2) suy ra C’D’ = A’B’ = AB = 2 cm.
Vậy CD = C’D’ = 2 cm.
Câu 2. Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm,
AE = 4 cm. Khẳng định đúng là:
A. HG = 4 cm, HE = 2 cm, GC = 4 cm;
B. HG = 2 cm, HE = 2 cm, GC = 4 cm;
C. HG = 4 cm, HE = 2 cm, GC = 2 cm;
D. HG = 4 cm, HE = 4 cm, GC = 4 cm.
Hướng dẫn giải
Đáp án: A
Giải thích:
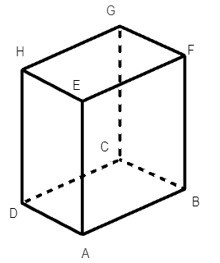
Từ hình hộp chữ nhật ABCD.EFGH ta có các mặt của hình hộp này đều là hình chữ nhật.
Khi đó ta có:
HG = DC = AB = 4 cm;
HE = DA = BC = 2 cm;
GC = HD = AE = 4 cm.
Vậy HG = 4 cm, HE = 2 cm, GC = 4 cm.
Câu 3. Cho hình hộp chữ nhật ABCD. EFGH. Chọn khẳng định đúng:
A. AE và BF cắt nhau;
B. ED và HA cắt nhau;
C. EF và GH cắt nhau;
D. AD và BC cắt nhau.
Hướng dẫn giải
Đáp án: B
Giải thích:
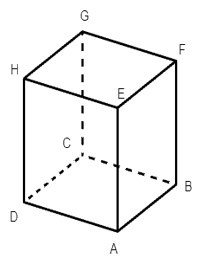
Vì ABCD. EFGH là hình hộp chữ nhật nên ta có:
• AEFB là hình chữ nhật suy ra AE // BF.
Do đó AE và BF không cắt nhau. Vậy A là một khẳng định sai.
• AEHD là hình chữ nhật mà ED và HA là hai đường chéo của hình chữ nhật này nên ED và HA cắt nhau. Vậy B là một khẳng định đúng.
• EFGH là hình chữ nhật suy ra EF // GH.
Do đó EF và GH không cắt nhau. Vậy C là một khẳng định sai.
• ABCD là hình chữ nhật suy ra AD // BC.
Do đó AD và BC không cắt nhau. Vậy D là một khẳng định sai.
Câu 4. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có ba kích thước khác nhau. Cạnh có độ dài bằng cạnh AA’ là:
A. AB;
B. BC;
C. BB’;
D. A’B’.
Hướng dẫn giải
Đáp án: C
Giải thích:
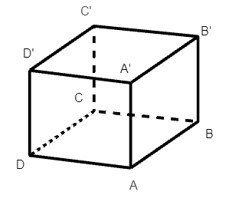
Ta có AA’, BB’, CC’, DD’ là các cạnh bên của hình hộp nên ta có:
AA’ = BB’ = CC’ = DD’.
Câu 5. Cho hình hộp chữ nhật ABCD. EFGH. Số đo góc BFG bằng
A. 30°;
B. 60°;
C. 90°;
D. 150°.
Hướng dẫn giải
Đáp án: C
Giải thích:
Xét hình hộp chữ nhật ABCD. EFGH:
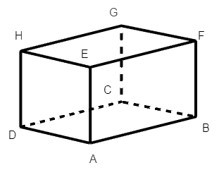
Có ba góc vuông ở đỉnh F là: góc EFG, góc BFE và góc BFG.
Do đó số đo của góc BFG bằng 90°.
Câu 6. Cho hình hộp chữ nhật ABCD. EFGH. Có bao nhiêu cạnh song song với cạnh AE?
A. 1;
B. 2;
C. 3;
D. 4.
Hướng dẫn giải
Đáp án: C
Giải thích:
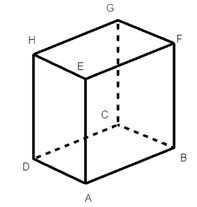
Từ hình hộp chữ nhật ABCD. EFGH ta có:
AEFB là hình chữ nhật suy ra AE // FB.
AEHD là hình chữ nhật suy ra AE // HD.
FBCG là hình chữ nhật suy ra FB // GC.
Mà FB // AE nên GC // AE.
Vậy có ba cạnh song song với AE là FB, HD, GC.
Câu 7. Cho hình hộp chữ nhật EFGH.MNPQ. Khẳng định đúng là:
A. HG = EF = MN = PQ;
B. HE = GF = PN = QM;
C. HQ = GP = FN = EM;
D. Cả A, B, C đều đúng.
Hướng dẫn giải
Đáp án: D
Giải thích:
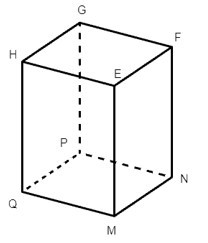
Các nhóm cạnh bằng nhau của hình hộp chữ nhật EFGH. MNPQ là:
HG = EF = MN = PQ; HE = GF = PN = QM; HQ = GP = FN = EM.
Do đó A, B, C đều là những khẳng định đúng.
III. Vận dụng
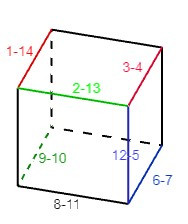
Câu 1. Phải gấp các cạnh nào của hình sau đây với nhau để được một hình lập phương?
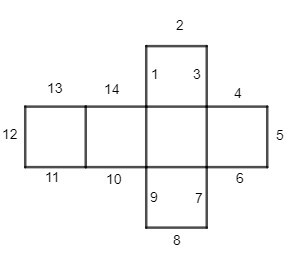
A. 12 và 5, 2 và 13, 1 và 14, 3 và 4, 8 và 11, 9 và 10, 7 và 6;
B. 12 và 5, 2 và 8, 1 và 14, 3 và 4, 13 và 11, 9 và 10, 7 và 6;
C. 12 và 5, 1 và 13, 2 và 14, 3 và 4, 8 và 11, 9 và 10, 7 và 6;
D. 14 và 5, 2 và 13, 1 và 12, 3 và 4, 8 và 11, 9 và 10, 7 và 6.
Hướng dẫn giải
Đáp án: A
Giải thích:
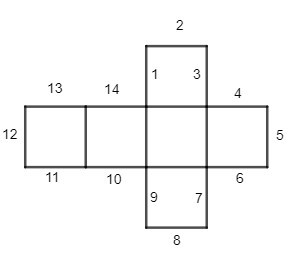
Ta phải gấp các cặp cạnh sau đây với nhau để hình trên trở thành một hình lập phương:
12 và 5, 2 và 13, 1 và 14, 3 và 4, 8 và 11, 9 và 10, 7 và 6.
Khi đó ta được hình vuông sau:
Câu 2. Tấm bìa nào sau đây gấp được hình hộp lập phương?
A. 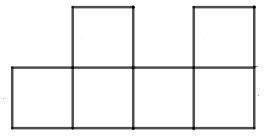
B. 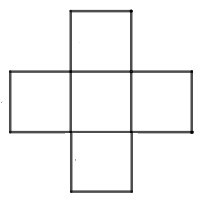
C. 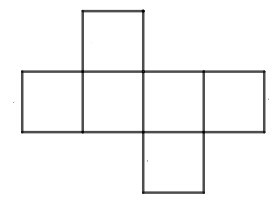
D. 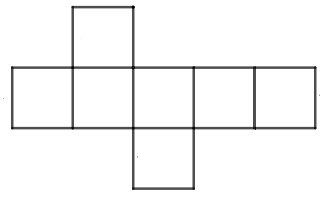
Hướng dẫn giải
Đáp án: C
Giải thích:
Hình lập phương là hình có 6 mặt.
Quan sát các hình ở từng đáp án ta thấy:
Hình B có tất cả 5 mặt nên không gấp được hình lập phương có 6 mặt. Do đó B sai.
Hình D có tất cả 7 mặt nên không gấp được hình lập phương có 6 mặt. Do đó D sai.
Hình A có hai mặt đáy trên nhưng không có mặt đáy dưới nên A sai.
Câu 3. Cho các miếng bìa sau:
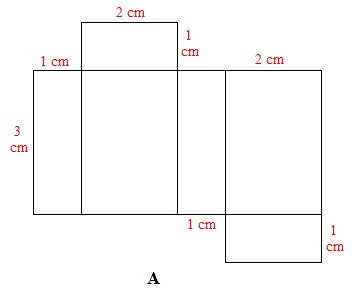
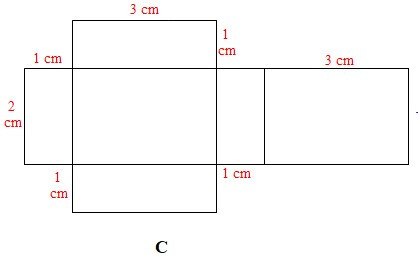
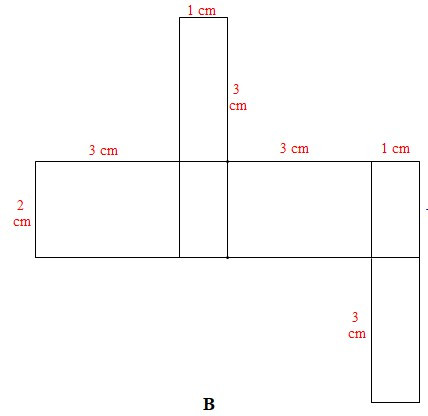
Có mấy tấm bìa gấp được hình hộp chữ nhật có ba kích thước 1 cm, 2 cm, 3 cm?
A. 1;
B. 2;
C. 3;
D. 4.
Hướng dẫn giải
Đáp án: C
Giải thích:
Xét miếng bìa A: Ta gấp được hình hộp chữ nhật sau:
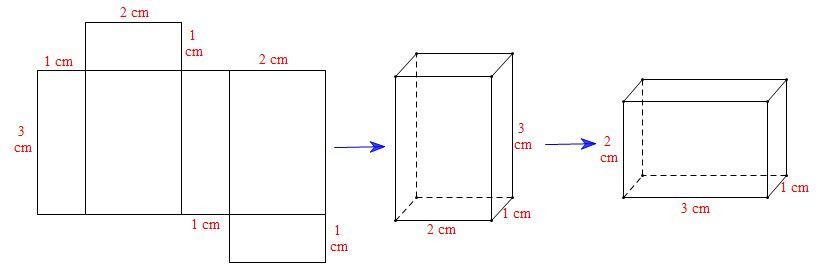
Xét miếng bìa B: Ta gấp được hình hộp chữ nhật sau:
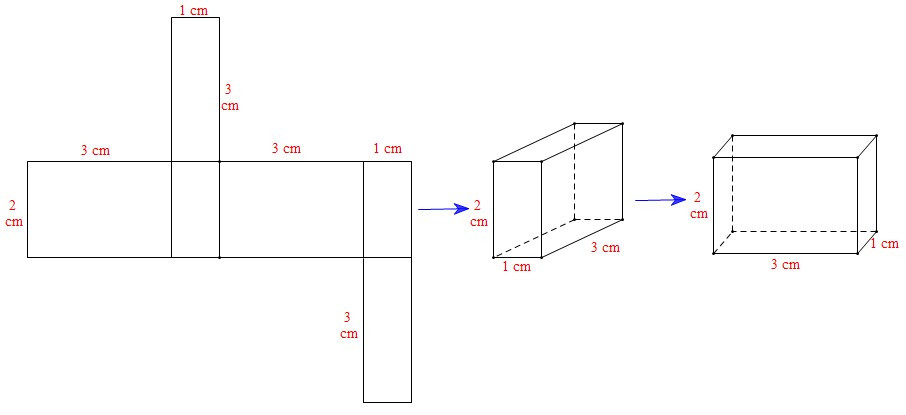
Xét miếng bìa C: Ta gấp được hình hộp chữ nhật sau:
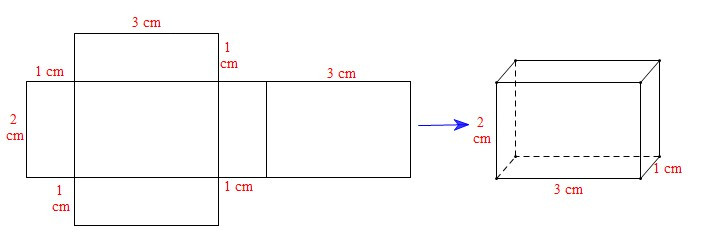
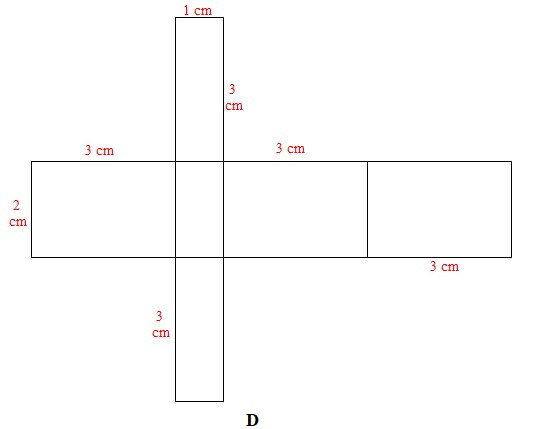
Xét miếng bìa D: Không gấp được hình hộp chữ nhật do chiều dài 3 cm của mặt (1) chưa hợp lí. Để gấp được hình hộp chữ nhật thì kích thước đó của mặt (1) bằng 1 cm.
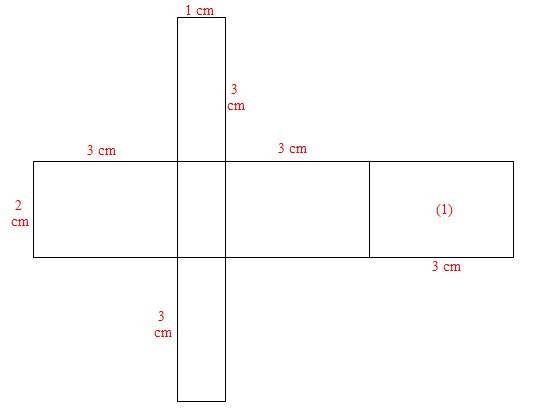
Vậy có 3 tấm bìa gấp được hình hộp chữ nhật có ba kích thước 1 cm, 2 cm, 3 cm.
Xem thêm các bài trắc nghiệm Toán 7 Chân trời sáng tạo hay, chi tiết khác:
Trắc nghiệm Ôn tập chương 2
Trắc nghiệm Bài 1. Hình hộp chữ nhật – Hình lập phương
Trắc nghiệm Bài 2. Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương
Trắc nghiệm Bài 3. Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
Trắc nghiệm Bài 4. Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác