Bộ 20 đề thi học kì 2 Toán 7 Kết nối tri thức có đáp án năm 2024

Chỉ từ 150k mua trọn bộ Đề thi học kì 2 Toán 7 Kết nối tri thức bản word có lời giải chi tiết ( cho 1 đề thi bất kì):

B1: –

B2: – nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Bộ 20 đề thi học kì 2 Toán lớp 7 Kết nối tri thức có đáp án năm 2023 – 2024 – Đề 1

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2 – Kết nối tri thức

Năm học 2023 – 2024

Môn: Toán 7

Thời gian làm bài: 90 phút

(Đề số 1)

I. TRẮC NGHIỆM (2 điểm)

Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Câu 1. Tam giác ABC có $B C = 1 c m, A C = 8 c m .$ Tìm độ dài cạnh AB, biết độ dài này là một số nguyên $(c m)$ .
A. 6cm B. 7cm C. 8cm D. 9cm

Câu 2. Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là B = {1; 2; 3; … ; 29,30}. Tính xác suất để kết quả rút ra là một thẻ có số chia hết cho 3

A. 6 B. 30 C. $\frac{1}{2}$ D. $\frac{1}{3}$

Câu 3. Cho $Δ A B C$ có $A B = 6 c m, B C = 8 c m, A C = 10 c m .$ Số đo góc $∠ A; ∠ B; ∠ C$ theo thứ tự là:
A. $∠ B < ∠ C < ∠ A$ B. $∠ C < ∠ A < ∠ B$

C. $∠ A > ∠ B > ∠ C$ D. $∠ C < ∠ B < ∠ A$

Câu 4. Khẳng định nào sau đây là đúng?

A. Số $0$ không phải là một đa thức.

B. Nếu $Δ A B C$ cân thì trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh cùng nằm trên một đường thẳng.

C. Nếu $Δ A B C$ cân thì trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh cùng nằm trên một đường tròn.

D. Số $0$ được gọi là một đa thức không và có bậc bằng $0$

Câu 5. Nghiệm của đa thức: $P (x) = 15 x - 3$ là:

A. $\frac{- 1}{5}$ B. $\frac{1}{5}$ C. $5$ D. $- 5$

Câu 6. Hình lăng trụ đứng tam giác có đáy là tam giác đều có cạnh bằng $3 c m$ , chiều cao hình lăng trụ bằng $10 c m$ . Diện tích xung quanh của hình lăng trụ đó là:

A. $30 c m^{2}$ B. $90 c m^{2}$ C. $90 c m^{3}$ D. $13 c m^{2}$

Câu 7. Bậc của đa thức $10 x^{7} + x^{8} - 2 x$ là:

A. $7$ B. $8$ C. $15$ D. $10$

Câu 8. Nếu đại lượng $y$ tỉ lệ thuận với đại lượng $x$ theo hệ số tỉ lệ là 2025 thì đại lượng $x$ tỉ lệ thuận với đại lượng $y$ theo hệ số tỉ lệ là:

A. $- \frac{1}{2025}$ B. $2025$ C. $\frac{1}{2025}$ D. $- 2025$

II. PHẦN TỰ LUẬN (8,0 điểm)

Bài 1. (0,75 điểm) Phần bên trong của một cái khuôn làm bánh (không có nắp) có dạng hình hộp chữ nhật với đáy là hình vuông cạnh là $20 c m,$ chiều cao $5 c m .$ Người ta dự định sơn phần bên trong bằng loại sơn không dính. Hỏi với một lượng sơn đủ bao phủ được $100 m^{2}$ thì sơn được bao nhiêu cái khuôn làm bánh?

Bài 2. (1,5 điểm) Hai ô tô khởi hành cùng một lúc $A$ đến $B$ . Xe thứ nhất đi từ $A$ đến $B$ hết $6$ giờ, xe thứ hai đi từ $B$ đến $A$ hết $3$ giờ. Đến chỗ gặp nhau, xe thứ hai đã đi được một quãng đường dài hơn xe thứ nhất đã đi là $54$ km. Tính quãng đường $A B$ .

Bài 3. (2,25 điểm) Cho các đa thức sau:

$P (x) = - 2 x + \frac{1}{2} x^{2} + 3 x^{4} - 3 x^{2} - 3$

$Q (x) = 3 x^{4} + x^{3} - 4 x^{2} + 1, 5 x^{3} - 3 x^{4} + 2 x + 1$

a) Thu gọn và sắp xếp các đa thức trên theo thứ tự số mũ của biến giảm dần. Xác định bậc, hệ số cao nhất và hệ số tự do của các đa thức đã cho.

b) Xác định $P (x) + Q (x)$ , $P (x) - Q (x)$ .

c) Xác định đa thức $R (x)$ thỏa mãn $R (x) + P (x) - Q (x) + x^{2} = 2 x^{3} - \frac{3}{2} x + 1$ .

Bài 4. (3 điểm) Cho tam giác ABC cân tại A.Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho AM + AN = 2AB.

a) Chứng minh rằng: BM = CN

b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN.

c) Đường trung trực của MN và tia phân giác của $\hat{B A C}$ cắt nhau tại K. Chứng minh rằng $Δ B K M = Δ C K N$ từ đó suy ra KC vuông góc với AN.

Bài 5. (0,5 điểm) Cho $a, b, c \neq 0$ và thỏa mãn $\frac{a + b - c}{c} = \frac{c + a - b}{b} = \frac{b + c - a}{a} .$ Tính giá trị của biểu thức $S = \frac{(a + b) (b + c) (c + a)}{a b c} .$

Hướng dẫn giải:

I. Trắc nghiệm

1. C	2. D	3. B	4. B
5. B	6. B	7. B	8. C

Câu 1.

Phương pháp:

Áp dụng bất đẳng thức tam giác để tìm cạnh còn lại.
Cách giải:

Áp dụng bất đẳng thức cho tam giác ABC ta có:

$\begin{array}{l} A C - B C < A B < A C + B C \\ \Rightarrow 8 - 1 < A B < 8 + 1 \\ \Rightarrow 7 < A B < 9 \\ \Rightarrow A B = 8 (c m) \end{array}$

Chọn C.

Câu 2.

Phương pháp:

Tìm các số chia hết cho 3 từ 0 đến 30

Cách giải:

Các số chia hết cho 3 từ tập B = {1; 2; 3; … ; 29,30} là 3,6,9,12,15,18,21,24,27,30

=> Có tất cả 10 số chia hết cho 3.

Vậy xác suất để thẻ rút ra là số chia hết cho 3 là: $\frac{10}{30} = \frac{1}{3}$

Chọn D.

Câu 3.

Phương pháp:

So sánh độ dài các cạnh rồi dựa vào mối quan hệ giữa cạnh và góc trong một tam giác để so sánh các góc với nhau. Trong một tam giác, góc đối diện với cạnh lớn hơn thì góc lớn hơn.
Cách giải:

$Δ A B C$ có $A B = 6 c m, B C = 8 c m, A C = 10 c m .$

Ta có: $A B < B C < A C$ $\Rightarrow ∠ C < ∠ A < ∠ B$

Chọn B.

Câu 4.

Phương pháp:

Áp dụng định nghĩa về đa thức và tính chất tam giác cân.
Cách giải:

Xét từng đáp án:

A. Số $0$ không phải là một đa thức. Sai Vì số 0 là đa thức 0

B. Nếu $Δ A B C$ cân thì trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh cùng nằm trên một đường thẳng. Đúng: (vẽ một tam giác cân và xác định trọng tâm, trực tâm, điểm cách đều 3 đỉnh, điểm nằm trong tam giác và cách đều 3 cạnh ta thấy chúng cùng nằm trên một đường thẳng)

C. Nếu $Δ A B C$ cân thì trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh cùng nằm trên một đường tròn. Sai Vì chúng nằm trên cùng 1 đường thẳng.

D. Số $0$ được gọi là một đa thức không và có bậc bằng 0. Sai Vì số 0 được gọi là đa thức không và nó là đa thức không có bậc.

Chọn B

Câu 5.

Phương pháp:

Tìm nghiệm của đa thức $P (x)$ , ta giải phương trình $P (x) = 0$

Cách giải:

Ta có: $P (x) = 0$

$\begin{array}{l} 15 x - 3 = 0 \\ 15 x = 3 \\ x = \frac{1}{5} \end{array}$

Vậy $x = \frac{1}{5}$ là nghiệm của đa thức $P (x) = 15 x - 3$

Chọn B.

Câu 6.

Phương pháp:

+ Tam giác đều có ba cạnh bằng nhau.

+ Diện tích xung quanh của hình lăng trụ đứng là: $S_{x q} = C$ _đáy $. h$

Cách giải:

Diện tích xung quanh của hình lăng trụ là: $S_{x q} = (3 + 3 + 3) .10 = 9.10 = 90 (c m^{2})$

Chọn B.

Câu 7.

Phương pháp:

Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó

Cách giải:

Ta có: hạng tử $x^{8}$ là có bậc cao nhất

$\Rightarrow$ Bậc của đa thức $10 x^{7} + x^{8} - 2 x$ là: $8$

Câu 8.

Phương pháp:

Nếu đại lượng $y$ tỉ lệ thuận với đại lượng $x$ theo hệ số tỉ lệ $k$ thì ta có công thức: $y = k x$

Cách giải:

Vì đại lượng $y$ tỉ lệ thuận với đại lượng $x$ theo hệ số tỉ lệ là 2025 nên ta có công thức: $y = 2025 x$

Từ đó suy ra $x = \frac{1}{2025} y$

Do đó, đại lượng $x$ tỉ lệ thuận với đại lượng $y$ theo hệ số tỉ lệ $\frac{1}{2025}$ .

Chọn C.

Chú ý: Nếu đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k thì đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ $\frac{1}{k}$ .

II. PHẦN TỰ LUẬN (8,0 điểm)

Bài 1.

Phương pháp:

Sử dụng công thức tính diện tích xung quanh của hình hộp chữ nhật.

Chú ý: Phải đưa về cùng đơn vị đo

Bước 1: Đổi $100 m^{2} = 1000000 c m^{2}$

Bước 2: Tính diện tích xung quanh của khuôn

Bước 3: Tính diện tích cần sơn của một khuôn

Bước 4: Tính số khuôn sơn được

Cách giải:

Đổi $100 m^{2} = 1000000 c m^{2}$

Diện tích xung quanh của chiếc khuôn là: $S_{x q} = 2. (20 + 20) .5 = 400 (c m^{2})$

Diện tích cần được sơn của một chiếc khuôn là: $S^{'} = S_{x q} + S = 400 + (20.20) = 800 (c m^{2})$

Số chiếc khuôn được sơn là: $1000000 : 800 = 1250$ (chiếc)

Bài 2.

Phương pháp:

Tính chất dãy tỉ số bằng nhau: $\frac{a}{b} = \frac{c}{d} = \frac{c - a}{d - b}$

Cách giải:

Gọi quãng đường của xe thứ nhất đi được từ $A$ đến chỗ gặp là $x$ (km) $(x > 0)$

Gọi quãng đường của xe thứ hai đi được từ $B$ đến chỗ gặp là $y$ (km) $(y > 0)$

Ta có: $\frac{x}{3} = \frac{y}{6}$

Quãng đường đi được của xe thứ hai dài hơn xe thứ nhất $54$ km nên $y - x = 54$

Áp dụng tính chất của dãy tỉ số bằng nhau ta có: $\frac{x}{3} = \frac{y}{6} = \frac{y - x}{6 - 3} = \frac{54}{3} = 18$

Do đó $\frac{x}{3} = 18 \Rightarrow x = 54$ (thỏa mãn)

$\frac{y}{6} = 18 \Rightarrow y = 108$ (thỏa mãn)

Quãng đường $A B$ dài là $54 + 108 = 162$ (km)

Vậy quãng đường $A B$ dài là $162$ (km).

Bài 3.

Phương pháp:

+ Để thu gọn đa thức ta thực hiện phép cộng các đơn thức đồng dạng.

+ Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.

+ Ta có thể mở rộng cộng (trừ) các đa thức dựa trên quy tắc “dấu ngoặc” và tính chất của các phép toán trên số.

+ Đối với đa thức một biến đã sắp xếp còn có thể cộng (trừ) bằng cách đặt tính theo cột dọc tương tự cộng (trừ) các số.

Cách giải:

$\begin{array}{l} P (x) = - 2 x + \frac{1}{2} x^{2} + 3 x^{4} - 3 x^{2} - 3 \\ = 3 x^{4} + \frac{1}{2} x^{2} - 3 x^{2} - 2 x - 3 \\ = 3 x^{4} - \frac{5}{2} x^{2} - 2 x - 3 \end{array}$

Vậy: $P$ có bậc là $4$ ; Hệ số cao nhất là $3$ ; Hệ số tự do là $- 3$

$\begin{array}{l} Q (x) = 3 x^{4} + x^{3} - 4 x^{2} + 1, 5 x^{3} - 3 x^{4} + 2 x + 1 \\ = 3 x^{4} - 3 x^{4} + x^{3} + 1, 5 x^{3} - 4 x^{2} + 2 x + 1 \\ = \frac{5}{2} x^{3} - 4 x^{2} + 2 x + 1 \end{array}$

Vậy: $Q$ có bậc là $3$ ; Hệ số cao nhất là $\frac{5}{2}$ ; Hệ số tự do là $1$

$\begin{array}{l} P (x) + Q (x) = (3 x^{4} - \frac{5}{2} x^{2} - 2 x - 3) + (\frac{5}{2} x^{3} - 4 x^{2} + 2 x + 1) \\ = 3 x^{4} + \frac{5}{2} x^{3} - \frac{5}{2} x^{2} - 4 x^{2} - 2 x + 2 x - 3 + 1 \end{array}$

$= 3 x^{4} + \frac{5}{2} x^{3} - \frac{13}{2} x^{2} - 2$

$\begin{array}{l} P (x) - Q (x) = (3 x^{4} - \frac{5}{2} x^{2} - 2 x - 3) - (\frac{5}{2} x^{3} - 4 x^{2} + 2 x + 1) \\ = 3 x^{4} - \frac{5}{2} x^{2} - 2 x - 3 - \frac{5}{2} x^{3} + 4 x^{2} - 2 x - 1 \end{array}$

$\begin{array}{l} = 3 x^{4} - \frac{5}{2} x^{3} - \frac{5}{2} x^{2} + 4 x^{2} - 2 x - 2 x - 3 - 1 \\ = 3 x^{4} - \frac{5}{2} x^{3} + \frac{3}{2} x^{2} - 4 x - 4 \end{array}$

c) $R (x) + P (x) - Q (x) + x^{2} = 2 x^{3} - \frac{3}{2} x + 1$

$\Leftrightarrow R (x) + (3 x^{4} + \frac{5}{2} x^{3} - \frac{13}{2} x^{2} - 2) - (3 x^{4} - \frac{5}{2} x^{3} + \frac{3}{2} x^{2} - 4 x - 4) + x^{2} = 2 x^{3} - \frac{3}{2} x + 1$

$\Leftrightarrow R (x) + 3 x^{4} - 3 x^{4} + \frac{5}{2} x^{3} + \frac{5}{2} x^{3} - \frac{13}{2} x^{2} - \frac{3}{2} x^{2} + x^{2} + 4 x - 2 + 4 = 2 x^{3} - \frac{3}{2} x + 1$

$\Leftrightarrow R (x) + 5 x^{3} - 7 x^{2} + 4 x + 2 = 2 x^{3} - \frac{3}{2} x + 1$

$\begin{array}{l} \Leftrightarrow R (x) = 2 x^{3} - \frac{3}{2} x + 1 - (5 x^{3} - 7 x^{2} + 4 x + 2) \\ \Leftrightarrow R (x) = 2 x^{3} - \frac{3}{2} x + 1 - 5 x^{3} + 7 x^{2} - 4 x - 2 \end{array}$

$\begin{array}{l} \Leftrightarrow R (x) = 2 x^{3} - 5 x^{3} + 7 x^{2} - \frac{3}{2} x - 4 x - 2 + 1 \\ \Leftrightarrow R (x) = - 3 x^{3} + 7 x^{2} - \frac{11}{2} x - 1 \end{array}$

Bài 4.

Phương pháp:

a) Sử dụng tính chất tam giác cân, sau đó dùng giả thiết đã cho lập luận để suy ra điều phải chứng minh.

b) Sử dụng các trường hợp bằng nhau của tam giác để suy ra các cặp tam giác bằng nhau, từ đó suy ra điều phải chứng minh.

c) Sử dụng các trường hợp bằng nhau của tam giác để chứng minh hai góc bằng nhau, sử dụng thêm tính chất hai góc kề bù để suy ra điều phải chứng minh.
Cách giải:

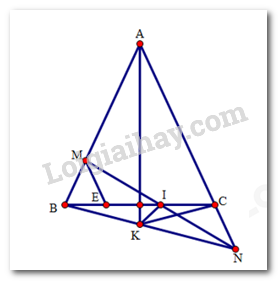
a) Do tam giác ABC cân tại A, suy ra AB = AC.

Ta có: AM + AN = AB – BM + AC + CN = 2AB – BM + CN.

Ta lại có AM + AN = 2AB(gt), nên suy ra $2 A B - B M + C N = 2 A B$ .

$\Leftrightarrow - B M + C N = 0 \Leftrightarrow B M = C N$

b) Gọi I là giao điểm của MN và BC. Vậy BM = CN (đpcm)

Qua M kẻ đường thẳng song song với AC cắt BC tại E.

Do ME // NC nên ta có:

$\hat{I M E} = \hat{C N I}$ (hai góc so le trong)

$\hat{M E I} = \hat{N C I}$ (hai góc so le trong)

$\hat{M E B} = \hat{A C B}$ (hai góc đồng vị) nên $\hat{M E B} = \hat{A B C} \Rightarrow Δ M B E$ cân tại M nên MB = ME. Do đó, ME = CN.

Ta chứng minh được $Δ M E I = Δ N C I (g . c . g)$

Suy ra MI = NI (hai cạnh tương ứng), từ đó suy ra I là trung điểm của MN.

c) Xét hai tam giác MIK và NIK có:

MI = IN (cmt), $\hat{M I K} = \hat{N I K} = 90^{0}$

IK là cạnh chung. Do đó $Δ M I K = Δ N I K (c . g . c)$ .

Suy ra KM = KN (hai cạnh tương ứng).

Xét hai tam giác ABK và ACK có:

AB = AC(gt),

$\hat{B A K} = \hat{C A K}$ (do BK là tia phân giác của góc BAC),

AK là cạnh chung,

Do đó $Δ A B K = Δ A C K (c . g . c)$ .

Suy ra KB = KC (hai cạnh tương ứng).

Xét hai tam giác BKM và CKN có:

MB = CN, BK = KN, MK = KC,

Do đó $Δ B K M = Δ C K N (c . c . c)$ ,

Suy ra $\hat{M B K} = \hat{K C N}$ .

Mà $\hat{M B K} = \hat{A C K} \Rightarrow \hat{A C K} = \hat{K C N} = 180^{0} : 2 = 90^{0} \Rightarrow K C ⊥ A N .$ (đpcm)

Bài 5.

Áp dụng tính chất của dãy tỉ số bằng nhau.

Cách giải:

– Trường hợp $1 : a, b, c \neq 0$ và $a + b + c = 0 \Rightarrow a + b = - c; a + c = - b; b + c = - a$ thay vảo biểu thức $S$ ta được:

$S = \frac{- c . (- a) . (- b)}{a b c} = - 1.$

– Trường hợp 2: $a, b, c \neq 0$ và $a + b + c \neq 0.$

Áp dụng tính chất của dãy tỉ số bằng nhau ta được:

$\frac{a + b - c}{c} = \frac{c + a - b}{b} = \frac{b + c - a}{a} = \frac{a + b - c + c + a - b + b + c - a}{c + b + a} = 1$

Suy ra ${\begin{cases} a + b = 2 c \\ c + a = 2 b \\ b + c = 2 a \end{cases}$ thay vào biểu thức $S$ ta được:

$S = \frac{2 c .2 a .2 b}{a b c} = 8$

Vậy: $S = - 1$ khi $\frac{a + b - c}{c} = \frac{c + a - b}{b} = \frac{b + c - a}{a}$ và $a, b, c \neq 0;$ $a + b + c = 0$

$S = 8$ khi $\frac{a + b - c}{c} = \frac{c + a - b}{b} = \frac{b + c - a}{a}$ và $a, b, c \neq 0;$ $a + b + c \neq 0$ .

A. Ma trận đề thi Học kì 2 môn Toán lớp 7 Kết nối tri thức

STT	Chương	Nội dung kiến thức	Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá								Tổng % điểm
			Nhận biết		Thông hiểu		Vận dụng		Vận dụng cao
			TN	TL	TN	TL	TN	TL	TN	TL
1	Tỉ lệ thức và đại lượng tỉ lệ	Tỉ lệ thức	1 (0,25đ)		1 (0,25đ)						17,5%
1	Tỉ lệ thức và đại lượng tỉ lệ	Tính chất dãy tỉ số bằng nhau và đại lượng tỉ lệ	1 (0,25đ)					1 (1,0đ)			17,5%
2	Biểu thức đại số và đa thức	Biểu thức đại số	1 (0,25đ)		1 (0,25đ)						32,5%
2	Biểu thức đại số và đa thức	Đa thức một biến	1 (0,25đ)			1 (1,0đ)		2 (1,0đ)		1 (0,5đ)	32,5%
3	Làm quen với biến cố và xác suất của biến cố	Biến cố		1 (0,75đ)							12,5%
3	Làm quen với biến cố và xác suất của biến cố	Xác suất của biến cố	1 (0,25đ)			1 (0,25đ)					12,5%
4	Quan hệ giữa các yếu tố trong một tam giác	Quan hệ giữa đường vuông góc và đường xiên. Các đường đồng quy của tam giác	3 (0,75đ)			1 (1,0đ)					32,5%
4	Quan hệ giữa các yếu tố trong một tam giác	Giải bài toán có nội dung hình học và vận dụng giải quyết vấn đề thực tiễn liên quan đến hình học				1 (1,0đ)		1 (0,5đ)			32,5%
5	Một số hình khối trong thực tiễn	Hình hộp chữ nhật và hình lập phương	1 (0,25đ)		1 (0,25đ)						5%
Tổng: Số câu Điểm			9 (2,25đ)	1 (0,75đ)	3 (0,75đ)	4 (3,25đ)		4 (2,5đ)		1 (0,5đ)	22 (10đ)
Tỉ lệ			30%		40%		25%		5%		100%
Tỉ lệ chung			70%				30%				100%

Lưu ý:

– Các câu hỏi trắc nghiệm khách quan là các câu hỏi ở mức độ nhận biết và thông hiểu, mỗi câu hỏi có 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.

– Các câu hỏi tự luận là các câu hỏi ở mức độ thông hiểu, vận dụng và vận dụng cao.

– Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ điểm được quy định trong ma trận.

B. Bảng đặc tả ma trận đề thi học kì 2 môn Toán lớp 7 Kết nối tri thức

STT	Chương	Nội dung kiến thức	Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá	Số câu hỏi theo mức độ
STT	Chương	Nội dung kiến thức	Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá	Nhận biết	Thông hiểu	Vận dụng	Vận dụng cao
1	Tỉ lệ thức và đại lượng tỉ lệ	Tỉ lệ thức	Nhận biết: – Nhận biết được tỉ lệ thức và các tính chất của tỉ lệ thức. Thông hiểu: – Tìm đại lượng chưa biết trong một tỉ lệ thức. Vận dụng: – Vận dụng được tính chất của tỉ lệ thức trong giải toán.	1TN	1TN
1	Tỉ lệ thức và đại lượng tỉ lệ	Tính chất dãy tỉ số bằng nhau và đại lượng tỉ lệ	Nhận biết : – Nhận biết được dãy tỉ số bằng nhau. – Nhận biết đại lượng tỉ lệ thuận, đại lượng tỉ lệ nghịch. – Chỉ ra hệ số tỉ lệ khi biết công thức. Thông hiểu: – Giải một số bài toán đơn giản về đại lượng tỉ lệ thuận, đại lượng tỉ lệ nghịch. Vận dụng: – Vận dụng được tính chất của dãy tỉ số bằng nhau trong giải toán (ví dụ: chia một số thành các phần tỉ lệ với các số cho trước,…). – Giải được một số bài toán về đại lượng tỉ lệ thuận (ví dụ: bài toán về tổng sản phẩm thu được và năng suất lao động,…). – Giải được một số bài toán về đại lượng tỉ lệ nghịch (ví dụ: bài toán về thời gian hoàn thành kế hoạch và năng suất lao động,…).	1TN		1TL
2	Biểu thức đại số và đa thức	Biểu thức đại số	Nhận biết: – Nhận biết được biểu thức số. – Nhận biết được biểu thức đại số. – Xác định biến số (biến) trong một biểu thức đại số. Thông hiểu: – Tính được giá trị của một biểu thức đại số. – Viết một biểu thức đại số biểu thị một mệnh đề.	1TN	1TN
2	Biểu thức đại số và đa thức	Đa thức một biến	Nhận biết: – Nhận biết đơn thức một biến và bậc của đơn thức. – Nhận biết đa thức một biến và các hạng tử của nó. – Nhận biết bậc, hệ số cao nhất, hệ số tự do của đa thức một biến. – Nhận biết được nghiệm của đa thức một biến. Thông hiểu: – Tính được giá trị của đa thức khi biết giá trị của biến. – Thu gọn và sắp xếp các hạng tử của một đa thức. Vận dụng: – Thực hiện được các phép tính: phép cộng, phép trừ phép nhân, phép chia trong tập hợp các đa thức một biến; vận dụng được những tính chất của các phép tính đó trong tính toán. – Tìm nghiệm của đa thức một biến. Vận dụng cao: – Xác định được hệ số của đa thức một biến để đa thức thỏa mãn yêu cầu. – Vận dụng tính chất của phép chia đa thức một biến để giải toán.	1TN	1TL	2TL	1TL
3	Làm quen với biến cố và xác suất của biến cố	Biến cố	Nhận biết: – Nhận biết biến cố chắc chắn, biến cố không thể, biến cố ngẫu nhiên.		1TL
3	Làm quen với biến cố và xác suất của biến cố	Xác suất của biến cố	Nhận biết: – Nhận biết được xác suất của một biến cố ngẫu nhiên. Thông hiểu: – Tính toán được xác suất của một biến cố ngẫu nhiên trong một số ví dụ đơn giản (ví dụ: lấy bóng trong túi, tung xúc xắc,…).	1TN	1TL
4	Quan hệ giữa các yếu tố trong một tam giác	Quan hệ giữa đường vuông góc và đường xiên. Các đường đồng quy của tam giác	Nhận biết: – Nhận biết quan hệ giữa góc và cạnh đối diện trong một tam giác. – Nhận biết liên hệ về độ dài của ba cạnh trong một tam giác. – Nhận biết đường vuông góc và đường xiên; khoảng cách từ một điểm đến một đường thẳng. – Nhận biết các đường đặc biệt trong tam giác (đường trung tuyến, đường cao, đường phân giác, đường trung trực); sự đồng quy của các đường đặc biệt đó. Thông hiểu: – Giải thích được quan hệ giữa đường vuông góc và đường xiên dựa trên mối quan hệ giữa cạnh và góc đối trong tam giác (đối diện với góc lớn hơn là cạnh lớn hơn và ngược lại).	3TN	1TL
		Giải bài toán có nội dung hình học và vận dụng giải quyết vấn đề thực tiễn liên quan đến hình học	Thông hiểu: – Giải thích được các trường hợp bằng nhau của hai tam giác, của hai tam giác vuông dựa trên tính chất của các đường đặc biệt trong tam giác. – Mô tả được tam giác cân và giải thích được tính chất của tam giác cân. Vận dụng: – Diễn đạt được lập luận và chứng minh hình học trong những trường hợp đơn giản (ví dụ: lập luận và chứng minh được các đoạn thẳng bằng nhau, các góc bằng nhau từ các điều kiện ban đầu liên quan đến tam giác,…). – Giải quyết được một số vấn đề thực tiễn (đơn giản, quen thuộc) liên quan đến ứng dụng của hình học như: đo, vẽ, tạo dựng các hình đã học. Vận dụng cao: – Giải quyết được một số vấn đề thực tiễn (phức hợp, không quen thuộc) liên quan đến ứng dụng của hình học như: đo, vẽ, tạo dựng các hình đã học.		1TL	1TL
5	Một số hình khối trong thực tiễn	Hình hộp chữ nhật và hình lập phương	Nhận biết Mô tả được một số yếu tố cơ bản (đỉnh, cạnh, góc, đường chéo) của hình hộp chữ nhật và hình lập phương. Thông hiểu – Giải quyết được một số vấn đề thực tiễn gắn với việc tính thể tích, diện tích xung quanh của hình hộp chữ nhật, hình lập phương (ví dụ: tính thể tích hoặc diện tích xung quanh của một số đồ vật quen thuộc có dạng hình hộp chữ nhật, hình lập phương,…).	1TN	1TN

Bộ 20 đề thi học kì 2 Toán lớp 7 Kết nối tri thức có đáp án năm 2023 – 2024 – Đề 2

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2 – Kết nối tri thức

Năm học 2023 – 2024

Môn: Toán 7

Thời gian làm bài: 90 phút

(Đề số 2)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Từ đẳng thức 8.6 = 4.12 ta lập được tỉ lệ thức là

A. $\frac{12}{4} = \frac{6}{8}$ ;

B. $\frac{8}{4} = \frac{12}{6}$ ;

C. $\frac{4}{12} = \frac{8}{6}$ ;

D. $\frac{4}{8} = \frac{12}{6}$ .

Câu 2. Cho tỉ lệ thức $\frac{x}{12} = \frac{- 2}{3}$ . Giá trị x là

A. ‒10;

B. ‒9;

C. ‒8;

D. ‒7.

Câu 3. Cho x và y là hai đại lượng tỉ lệ nghịch, biết khi x = 6 thì y = 5. Hệ số tỉ lệ nghịch a của x đối với y bằng bao nhiêu?

A. $a = \frac{6}{5}$ ;

B. $a = \frac{5}{6}$ ;

C. $a = \frac{1}{30}$ ;

D. a = 30.

Câu 4. Trong các đa thức sau, đa thức nào không phải là đa thức một biến?

A. x³ – 2xy;

B. 2y³ – 3y;

C. 3z²;

C. 4x – 5.

Câu 5. Giá trị của biểu thức 2x³y – 4y² + 1 tại x = –2 và y = –1 là

A. –13;

B. 13;

C. –19;

D. 19.

Câu 6. Cho đa thức P(x) = 2x⁴ – 3x² + x – 7x⁴. Hệ số cao nhất của đa thức là:

A. –7;

B. –5;

C. 2;

D. 4.

Câu 7. Rút ngẫu nhiên một chiếc bút từ một túi gồm 2 chiếc bút chì, 3 chiếc bút máy. Gọi A là biến cố “Rút được chiếc bút chì”, B là biến cố “Rút được chiếc bút máy”. Khẳng định nào sau đây là đúng?

A. P(A) = 1;

B. P(A) > P(B);

C. P(A) < P(B);

D. P(B) = 1.

Câu 8. Cho tam giác DEF có DE < DF < EF và DE = a, DF = b, EF = c. Khẳng định nào dưới đây là sai?

A. a > c – b;

B. a + b < c;

C. a < b + c;

D. a + b > c.

Câu 9. Cho tam giác có số đo ba góc lần lượt là 55°, 60°, 65°. Cạnh có độ dài lớn nhất là

A. Cạnh đối diện với góc có số đo là 65°;

B. Cạnh đối diện với góc có số đo là 60°;

C. Cạnh đối diện với góc có số đo là 55°;

D. Ba cạnh bằng nhau.

Câu 10. Cho tam giác ABC, ba đường cao của tam giác ABC cùng đi qua điểm I. Khẳng định nào sau đây là đúng?

A. I cách đều ba cạnh của tam giác ABC;

B. I cách đều ba đỉnh của tam giác ABC;

C. I là trọng tâm của tam giác ABC;

D. I là trực tâm của tam giác ABC.

Câu 11. Khẳng định nào dưới đây là sai?

A. Hình hộp chữ nhật có 8 đỉnh;

B. Hình hộp chữ nhật có 12 cạnh;

C. Hình hộp chữ nhật có 6 cạnh;

D. Hình hộp chữ nhật có 6 mặt.

Câu 12. Một hình lập phương có diện tích xung quanh là 100 cm². Độ dài cạnh của hình lập phương đó là:

A. 2 cm;

B. 4 cm;

C. 5 cm;

D. 10 cm.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (2,0 điểm) Cho hai đa thức P(x) = x² + 2x – 5 và Q(x) = x² – 9x + 5.

a) Tính M(x) = P(x) + Q(x) và N(x) = P(x) – Q(x).

b) Tìm nghiệm của các đa thức M(x), N(x).

c) Tìm đa thức R(x) biết R(x) = M(x).N(x).

Bài 2. (1,0 điểm) Có bốn đội máy san đất làm bốn khối lượng công việc như nhau. Biết đội thứ nhất hoàn thành công việc trong 4 ngày, đội thứ hai hoàn thành công việc trong 6 ngày, đội thứ ba hoàn thành công việc trong 10 ngày, đội thứ tư hoàn thành công việc trong 12 ngày. Hỏi mỗi đội có bao nhiêu máy san đất? biết rằng cả bốn đội có 72 máy và các máy có cùng năng suất.

Bài 3. (1,0 điểm) Một thùng kín có 15 quả bóng màu đỏ và 15 quả bóng màu xanh. Tuấn lấy ngẫu nhiên một quả bóng trong thùng. Xét các biến cố sau:

A: “Lấy được quả bóng màu đỏ hoặc màu xanh”;

B: “Lấy được quả bóng màu vàng”;

C: “Lấy được quả bóng màu đỏ”.

a) Trong các biến cố trên, biến cố nào là biến cố chắc chắn, biến cố không thể, biến cố ngẫu nhiên?

b) Tính xác suất của biến cố C.

Bài 4. (2,5 điểm) Cho tam giác ABC vuông tại C có góc A bằng 60°. Tia phân giác góc BAC cắt BC tại E. Kẻ EK vuông góc với AB tại K.

a) Chứng minh rằng AC = AK và CK ⊥ AE.

b) Chứng minh rằng AB = 2AC và EB > AC.

c) Kẻ BD vuông góc với AE tại D. Chứng minh ba đường thẳng AC, EK, BD đồng quy.

Bài 5. (0,5 điểm) Tìm a để đa thức 3x³ + 2x² – 7x + a chia hết cho đa thức x – 1.

Bộ 20 đề thi học kì 2 Toán lớp 7 Kết nối tri thức có đáp án năm 2023 – 2024 – Đề 3

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2 – Kết nối tri thức

Năm học 2023 – 2024

Môn: Toán 7

Thời gian làm bài: 90 phút

(Đề số 3)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Từ đẳng thức 2.15 = 6.5 lập được tỉ lệ thức nào sau đây?

A. $\frac{5}{15} = \frac{6}{2}$ ;

B. $\frac{2}{5} = \frac{6}{15}$ ;

C. $\frac{2}{15} = \frac{5}{6}$ ;

D. $\frac{5}{6} = \frac{15}{2}$ .

Câu 2. Giá trị nào của x thỏa mãn $\frac{x - 1}{6} = \frac{x - 5}{7}$ ?

A. x = –27;

B. x = –23;

C. x = 23;

D. x = 27.

Câu 3. Đại lượng y tỉ lệ nghịch với đại lượng x nếu:

A. x = ay với hằng số a ≠ 0;

B. $y = \frac{a}{x}$ với hằng số a ≠ 0;

C. y = ax với hằng số a ≠ 0;

D. $y = \frac{x}{a}$ với hằng số a ≠ 0.

Câu 4. Trong các biểu thức sau, biểu thức nào là biểu thức số?

A. 3²− 4;

B. x – 6 + y;

C. x² + x;

D. $\frac{1}{x} + x + 1$ .

Câu 5. Cho hai biểu thức: E = 2(a + b) – 4a + 3 và F = 5b – (a – b).

Khi a = 5 và b = –1. Chọn khẳng định đúng:

A. E = F;

B. E > F;

C. E < F;

D. E ≈ F.

Câu 6. Giá trị x = ‒ 1 là nghiệm của đa thức nào sau đây?

A. M(x) = x – 1;

B. N(x) = x + 1;

C. P(x) = x;

D. Q(x) = – x.

Câu 7. Trong một phép thử, bạn An xác định được biến cố M, biến cố N có xác suất lần lượt là $\frac{1}{3}$ và $\frac{1}{2}$ . Hỏi biến cố nào có khả năng xảy ra thấp hơn?

A. Biến cố M;

B. Biến cố N;

C. Cả hai biến cố M và N đều có khả năng xảy ra bằng nhau;

D. Không thể xác định được.

Câu 8. Khẳng định nào sau đây là đúng?

A. Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh nhỏ hơn;

B. Trong một tam giác, góc đối diện với cạnh nhỏ hơn là góc lớn hơn;

C. Trong một tam giác vuông, cạnh huyền là cạnh nhỏ nhất;

D. Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

Câu 9. Cho ∆ABC có AB > BC > AC. Chọn khẳng định sai:

A. AB < BC – AC;

B. AB > BC – AC;

C. AC > AB – BC;

D. AC < AB + BC.

Câu 10. Cho tam giác ABC. Ba đường trung trực của tam giác ABC cùng đi qua một điểm M. Khẳng định nào sau đây là đúng?

A. M cách đều ba đỉnh của tam giác ABC;

B. M cách đều ba cạnh của tam giác ABC;

C. M là trọng tâm tam giác ABC;

D. M là trực tâm tam giác ABC.

Câu 11. Hình hộp chữ nhật, hình lập phương không có chung đặc điểm nào dưới đây?

A. Các cạnh bằng nhau;

B. Các mặt đáy song song;

C. Các cạnh bên song song với nhau;

D. Có 8 đỉnh.

Câu 12. Một hình hộp chữ nhật có diện tích xung quanh là 180 cm², độ dài hai cạnh đáy là 8 cm và 10 cm. Chiều cao của hình hộp chữ nhật đó là

A. 2 cm;

B. 4 cm;

C. 5 cm;

D. 10 cm.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (2,0 điểm) Cho đa thức A(x) = –11x⁵ + 4x – 12x² + 11x⁵ + 13x² – 7x + 2.

a) Thu gọn, sắp xếp đa thức A(x) theo số mũ giảm dần của biến rồi tìm bậc, hệ số cao nhất của đa thức.

b) Tìm đa thức M(x) sao cho M(x) = A(x).B(x), biết B(x) = x – 1.

c) Tìm nghiệm của đa thức A(x).

Bài 2. (1,0 điểm) Ba đội công nhân cùng chuyển một khối lượng gạch như nhau. Thời gian để đội thứ nhất, đội thứ hai và đội thứ ba làm xong công việc lần lượt là 2 giờ, 3 giờ, 4 giờ. Tính số công nhân tham gia làm việc của mỗi đội, biết rằng số công nhân của đội thứ ba ít hơn số công nhân của đội thứ hai là 5 người và năng suất lao động của các công nhân là như nhau.

Bài 3. (1,0 điểm) Chọn ngẫu nhiên một số trong tập hợp M = {2; 3; 5; 6; 8; 9}.

a) Trong các biến cố sau, biến cố nào là biến cố chắc chắn? Biến cố nào là biến cố không thể và biến cố nào là biến cố ngẫu nhiên?

A: “Số được chọn là số nguyên tố”;

B: “Số được chọn là số có một chữ số”;

C: “Số được chọn là số tròn chục”.

b) Tính xác suất của biến cố A.

Bài 4. (2,5 điểm) Cho tam giác ABC vuông tại A, đường phân giác BD (D ∈ AC). Từ D kẻ DH vuông góc với BC.

a) Chứng minh ΔABD = ΔHBD.

b) So sánh AD và DC.

c) Gọi K là giao điểm của đường thẳng AB và DH, I là trung điểm của KC. Chứng minh 3 điểm B, D, I thẳng hàng.

Bài 5. (0,5 điểm) Tìm các giá trị nguyên của n để 2n² – n + 2 chia hết cho 2n + 1.

Đáp án đề thi Học kì 2 môn Toán lớp 7 Kết nối tri thức – Đề số 3

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Bảng đáp án:

Câu	1	2	3	4	5	6	7	8	9	10	11	12
Đáp án	B	B	B	A	B	B	A	D	A	A	A	C

Hướng dẫn giải phần trắc nghiệm

Câu 1.

Đáp án đúng là: B

Từ đẳng thức 2.15 = 6.5 ta lập được tỉ lệ thức là: $\frac{2}{5} = \frac{6}{15}$ .

Câu 2.

Đáp án đúng là: B

Từ $\frac{x - 1}{6} = \frac{x - 5}{7}$ suy ra:

7.(x – 1) = 6.(x – 5)

7x – 7 = 6x – 30

x = –23

Vậy x = –23.

Câu 3.

Đáp án đúng là: B

Khái niệm hai đại lượng tỉ lệ nghịch:

Nếu đại lượng y liên hệ với đại lượng x theo công thức $y = \frac{a}{x}$ hay xy = a (với a là một hằng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.

Câu 4.

Đáp án đúng là: A

Biểu thức 3²− 4 là biểu thức chứa các số nên là biểu thức số.

Biểu thức x – 6 + y; x² + x; $\frac{1}{x} + x + 1$ có chứa chữ nên không là biểu thức số.

Câu 5.

Đáp án đúng là: B

Thay a = 5 và b = –1 vào biểu thức E, ta được:

E = 2 . [5 + (−1)] – 4 . 5 + 3

= 2 . 4 – 4 . 5 + 3

= 8 – 20 + 3

= –9.

Thay a = 5 và b = –1 vào biểu thức F, ta được:

F = 5 . (–1) – [5 – (–1)]

= –5 – (5 + 1)

= –5 – 6

= –11

Vì –9 > –11 nên E > F.

Vậy ta chọn phương án B.

Câu 6.

Đáp án đúng là: B

Thay x = ‒ 1 lần lượt vào các đa thức ta thấy N(‒1) = 0, do đó x = ‒ 1 là nghiệm của đa thức N(x).

Câu 7.

Đáp án đúng là: A

Vì $\frac{1}{3} < \frac{1}{2}$ nên xác suất xảy ra biến cố M nhỏ hơn xác suất xảy ra biến cố N.

Do đó biến cố M có khả năng xảy ra thấp hơn biến cố N.

Câu 8.

Đáp án đúng là: D

Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn; góc đối diện với cạnh nhỏ hơn là góc nhỏ hơn.

Trong một tam giác vuông, cạnh huyền là cạnh lớn nhất.

Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

Vậy ta chọn phương án D.

Câu 9.

Đáp án đúng là: A

Ta có AB > BC – AC, nên B đúng;

AC > AB – BC, nên C đúng.

AC < AB + BC, nên D đúng;

AB < BC – AC, nên A sai.

Vậy ta chọn phương án A.

Câu 10.

Đáp án đúng là: A

Ba đường trung trực của tam giác ABC cùng đi qua một điểm M, điểm M này cách đều ba đỉnh của tam giác ABC.

Câu 11.

Đáp án đúng là: A

Chỉ có hình lập phương có tất cả các cạnh bằng nhau. Vậy hình hộp chữ nhật, hình lập phương không có chung đặc điểm các cạnh bằng nhau.

Câu 12.

Đáp án đúng là: C

Chu vi đáy của hình hộp chữ nhật là: 2 . (8 + 10) = 36 (cm).

Chiều cao của hình hộp chữ nhật đó là: 180 : 36 = 5 (cm).

PHẦN II. TỰ LUẬN (7,0 điểm)

Hướng dẫn giải phần tự luận

Bài 1. (2,0 điểm)

a) Ta có:

A(x) = –11x⁵ + 4x – 12x² + 11x⁵ + 13x² – 7x + 2

= x² – 3x + 2.

Đa thức A(x) có bậc là 2 và hệ số cao nhất là 1.

b) M(x) = A(x).B(x)

= (x² – 3x + 2).(x – 1)

= x.(x² – 3x + 2) – 1.(x² – 3x + 2)

= x³ – 3x² + 2x – x² + 3x – 2

= x² – 4x² + 5x – 2.

c) A(x) = 0

x² – 3x + 2 = 0

x² – x – 2x + 2 = 0

x(x – 1) – 2(x – 1) = 0

(x – 1)(x – 2) = 0

x = 1 hoặc x = 2.

Vậy đa thức A(x) có nghiệm là x ∈ {1; 2}.

Bài 2. (1,0 điểm)

Gọi số công nhân tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là x, y, z.

Số công nhân của đội thứ ba ít hơn số công nhân của đội thứ hai là 5 người nên y – z = 5.

Với cùng một khối lượng công việc, số công nhân tham gia làm việc và thời gian hoàn thanh công việc của mỗi đội là hai đại lượng tỉ lệ nghịch với nhau.

Do đó, ta có 2x = 3y = 4z suy ra $\frac{x}{\frac{1}{2}} = \frac{y}{\frac{1}{3}} = \frac{z}{\frac{1}{4}}$ .

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

$\frac{x}{\frac{1}{2}} = \frac{y}{\frac{1}{3}} = \frac{z}{\frac{1}{4}} = \frac{y - z}{\frac{1}{3} - \frac{1}{4}} = \frac{5}{\frac{1}{12}} = 60$ .

Từ đó suy ra $x = 60. \frac{1}{2} = 30$ , $y = 60. \frac{1}{3} = 20$ , $z = 60. \frac{1}{4} = 15$ .

Vậy số công nhân tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là 30 người, 20 người, 15 người.

Bài 3. (1,0 điểm) M = {2; 3; 5; 6; 8; 9}.

a) Tập hợp M gồm có số nguyên tố và hợp số nên biến cố A là biến cố ngẫu nhiên.

Trong tập hợp M, tất cả các số đều là số có một chữ số nên biến cố B là biến cố chắc chắn.

Trong tập hợp M, không có số nào là số tròn chục nên biến cố C là biến cố không thể.

b) Trong tập hợp M gồm 6 số, có 3 số là số nguyên tố, đó là số 2; 3; 5.

Xác suất của biến cố A là: $\frac{3}{6} = \frac{1}{2}$ .

Bài 4. (2,5 điểm)

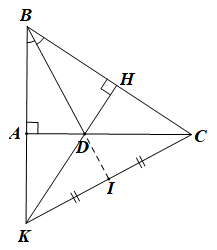
Bộ 30 đề thi Học kì 2 Toán lớp 7 Kết nối tri thức có đáp án (ảnh 1)

a) Xét DABD và ΔHBD có:

$\hat{B A D} = \hat{B H D} = 90 °$ ,

BD là cạnh chung,

$\hat{A B D} = \hat{H B D}$ (do BD là tia phân giác của ).

Do đó DABD = ΔHBD (cạnh huyền – góc nhọn).

b) Từ DABD = ΔHBD (câu a) suy ra AD = HD (hai cạnh tương ứng)

Xét DDHC vuông tại H có DC là cạnh huyền nên DC là cạnh lớn nhất

Do đó DC > HD nên DC > AD.

c) Xét DBKC có CA ⊥ BK, KH ⊥ BC và CA cắt KH tại D

Do đó D là trực tâm của DBKC, nên BD ⊥ KC (1)

Gọi J là giao điểm của BD và KC.

Xét DBKJ và DBCJ có:

$\hat{B J K} = \hat{B J C} = 90 °$ ,

BJ là cạnh chung,

$\hat{K B J} = \hat{C B J}$ (do BJ là tia phân giác của $\hat{A B D}$ ).

Do đó DBKJ = DBCJ (cạnh góc vuông – góc nhọn kề)

Suy ra KJ = CJ (hai cạnh tương ứng)

Hay J là trung điểm của KC.

Mà theo bài I là trung điểm của KC nên I và J trùng nhau.

Do đó ba điểm B, D, I thẳng hàng.

Bài 5. (0,5 điểm)

Thực hiện phép chia đa thức 2n² – n + 2 cho đa thức 2n + 1 như sau:

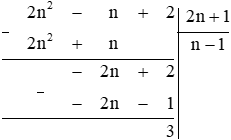
Bộ 30 đề thi Học kì 2 Toán lớp 7 Kết nối tri thức có đáp án (ảnh 1)

Để 2n² – n + 2 chia hết cho 2n + 1 thì (2n + 1) ∈ Ư(3) = {1; ‒1; 3; ‒3}.

Ta có bảng sau:

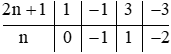
Bộ 30 đề thi Học kì 2 Toán lớp 7 Kết nối tri thức có đáp án (ảnh 1)

Vậy n ∈ {–2; –1; 0; 1}.

Bộ 20 đề thi học kì 2 Toán lớp 7 Kết nối tri thức có đáp án năm 2023 – 2024 – Đề 4

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2 – Kết nối tri thức

Năm học 2023 – 2024

Môn: Toán 7

Thời gian làm bài: 90 phút

(Đề số 4)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Tỉ lệ thức nào sau đây không được lập từ tỉ lệ thức $\frac{16}{10} = \frac{24}{15}$ ?

A. $\frac{16}{24} = \frac{10}{15}$ ;

B. $\frac{24}{16} = \frac{15}{10}$ ;

C. $\frac{24}{10} = \frac{16}{15}$ ;

D. $\frac{15}{24} = \frac{10}{16}$ .

Câu 2. Giá trị của x thỏa mãn $\frac{x + 1}{8} = \frac{18}{16}$ là:

A. 4;

B. 5;

C. 7;

D. 8.

Câu 3. Khi $\frac{a}{x}$ (a ≠ 0) thì ta nói

A. y tỉ lệ với x;

B. y tỉ lệ nghịch với x theo hệ số tỉ lệ a;

C. y tỉ lệ thuận với x theo hệ số tỉ lệ a;

D. y tỉ lệ thuận với x.

Câu 4. Cho biểu thức đại số ax² + by + 22, với a, b là hằng số. Các biến trong biểu thức đại số đã cho là

A. x và y;

B. b và 22;

C. y và a;

D. x, y và a.

Câu 5. Giá trị của biểu thức x² – 2x + 1 tại x = 0,5 là

A. $\frac{- 1}{4}$ ;

B. $\frac{1}{4}$ ;

C. – 1;

D. 1.

Câu 6. Kết quả của (3x²).(–2x) là

A. –6x³;

B. 6x³;

C. –6x²;

D. 3x³.

Câu 7. Khẳng định nào sau đây không đúng?

A. Xác suất của một biến cố là một số nằm từ 0 đến 1;

B. Các biến cố đồng khả năng có xác suất bằng nhau;

C. Biến cố có xác suất càng lớn càng dễ xảy ra;

D. Xác suất của biến cố chắc chắn bằng 0.

Câu 8. Cho tam giác ABM có $\hat{B} = 100 °$ . Khẳng định nào dưới đây là đúng?

A. AM > AB;

B. AM < AB;

C. AM = AB;

D. AM < BM.

Câu 9. Bộ ba nào trong các bộ ba đoạn thẳng có độ dài dưới đây là ba cạnh của tam giác?

A. 3 cm, 2 cm, 9 cm;

B. 1 cm, 5 cm, 7 cm;

C. 4 cm, 6 cm, 10 cm;

D. 5 cm, 4 cm, 2 cm.

Câu 10. Cho tam giác ABC, hai đường trung tuyến AM, BN cắt nhau tại G. Biết CG = 4, độ dài đường trung tuyến xuất phát từ C bằng

A. 2;

B. 3;

C. 6;

D. 8.

Câu 11. Các mặt của hình lập phương đều là

A. Hình vuông;

B. Hình lập phương;

C. Hình chữ nhật;

D. Hình thoi.

Câu 12. Một hộp sữa tươi dạng hình hộp chữ nhật với các kích thước của đáy là 4 cm, 5 cm và chiều cao là 10 cm. Thể tích của hộp sữa đó là

A. 90 cm³;

B, 100 cm³;

C. 180 cm³;

D. 200 cm³.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (2,0 điểm) Cho hai đa thức P(x) = 5x³ – 3x + 7 – x;

Q(x) = –5x³ + 2x – 3 + 2x – x² – 2.

a) Thu gọn hai đa thức P(x), Q(x) và xác định bậc của hai đa thức đó.

b) Tìm đa thức M(x) sao cho P(x) = M(x) – Q(x).

c) Tìm nghiệm của đa thức M(x).

Bài 2. (1,0 điểm) Ba lớp 7A, 7B, 7C tham gia trồng cây. Biết rằng số cây lớp 7A, 7B, 7C trồng được lần lượt tỉ lệ với 6; 4; 5 và tổng số cây của lớp 7B và 7C trồng được nhiều hơn của lớp 7A và 15 cây. Tính số cây mỗi lớp trồng được.

Bài 3. (1,0 điểm) Chọn ngẫu nhiên một số trong tập hợp {3; 5; 6; 7; 8; 10; 11}.

Xét các biến cố sau:

A: “Số được chọn là số nguyên tố”;

B: “Số được chọn là số bé hơn 12”;

C: “Số được chọn là số chính phương”.

a) Trong các biến cố trên, biến cố nào là biến cố chắc chắn, biến cố không thể, biến cố ngẫu nhiên?

b) Tìm xác suất của biến cố D: “Số được chọn là số chẵn”.

Bài 4. (2,5 điểm) Cho tam giác ABC vuông tại A có $\hat{B} = 60 °$ , đường cao AH. Trên tia đối của tia HB lấy điểm M sao cho HM = HB.

a) Chứng minh rằng HB < HC.

b) Chứng minh rằng DAHB = DAHM. Từ đó suy ra DABM là tam giác đều.

c) Gọi N là trung điểm của AC và O là giao điểm của AM và BN. Biết AB = 4 cm, tính độ dài đoạn thẳng AO.

Bài 5. (0,5 điểm) Tìm x, y thỏa mãn: x² + 2x²y² + 2y² – (x²y² + 2x²) – 2 = 0.

Bộ 10 đề thi học kì 2 Toán lớp 7 Kết nối tri thức có đáp án năm 2023 – 2024 – Đề 5

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2 – Kết nối tri thức

Năm học 2023 – 2024

Môn: Toán 7

Thời gian làm bài: 90 phút

(Đề số 5)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Từ đẳng thức $\frac{4}{- 5, 12} = \frac{2, 5}{- 3, 2}$ lập được tỉ lệ thức nào sau đây.

A. $\frac{- 3, 2}{- 5, 12} = \frac{2, 5}{4}$ ;

B. $\frac{- 5, 12}{4} = \frac{2, 5}{- 3, 2}$ ;

C. $\frac{2, 5}{- 5, 12} = \frac{4}{- 3, 2}$ ;

D. $\frac{- 5, 12}{2, 5} = \frac{4}{- 3, 2}$ .

Câu 2. Số hữu tỉ x trong tỉ lệ thức sau: $\frac{2 x + 3}{24} = \frac{3 x - 1}{32}$ là

A. x = –15;

B. x = 15;

C. x = –120;

D. x = 120.

Câu 3. Phát biểu nào sau đây sai?

A. Nếu x = –5y thì ta nói x tỉ lệ thuận với y theo hệ số tỉ lệ –5;

B. Nếu $a = \frac{3}{b}$ thì ta nói b tỉ lệ nghịch với a theo hệ số tỉ lệ 3;

C. Nếu m = n thì ta nói n tỉ lệ thuận với m theo hệ số tỉ lệ 1;

D. Nếu g = 0.h thì ta nói g tỉ lệ nghịch với h theo hệ số tỉ lệ 0.

Câu 4. Biểu thức nào sau đây là biểu thức số?

A. $\frac{1}{x} + y$ ;

B. xy;

C. x² + y²;

D. 16.(3² + 4).

Câu 5. Cho biểu thức C = –y² + 3x³ + 10. Giá trị của biểu thức C tại x = –1; y = 2 là

A. 9;

B. 11;

C. 3;

D. –3.

Câu 6. Đa thức nào sau đây có bậc là 0?

A. 0;

B. 14;

C. x;

D. 2x – x.

Câu 7. Cho các phát biểu sau:

(I) Biến cố có khả năng xảy ra cao hơn sẽ có xác suất lớn hơn;

(II) Xác suất xảy ra của mỗi kết quả là $\frac{1}{n}$ , trong đó n là số các kết quả có khả năng xảy ra bằng nhau của một trò chơi.

Chọn kết luận đúng:

A. Chỉ (I) đúng;

B. Chỉ (II) đúng;

C. Cả (I) và (II) đều đúng;

D. Cả (I) và (II) đều sai.

Câu 8. Cho tam giác ABC có AB = 5 cm, BC = 9 cm và CA = 13 cm. Sắp xếp các góc của ∆ABC theo số đo giảm dần là

A. $\hat{A}; \hat{B}; \hat{C}$ ;

B. $\hat{B}; \hat{A}; \hat{C}$ ;

C. $\hat{A}; \hat{C}; \hat{B}$ ;

D. $\hat{C}; \hat{B}; \hat{A}$ .

Câu 9. Bộ ba độ dài nào dưới đây không thể là độ dài ba cạnh của một tam giác?

A. 2 cm, 5 cm, 7 cm;

B. 3 cm, 5 cm, 7 cm;

C. 4 cm, 5 cm, 6 cm;

D. 3 cm, 5 cm, 6 cm.

Câu 10. Trong một tam giác, trực tâm là giao điểm của ba đường gì?

A. Trung trực;

B. Phân giác;

C. Trung tuyến;

D. Đường cao.

Câu 11. Hình lập phương không có đặc điểm nào sau đây?

A. Có 12 cạnh bằng nhau;

B. Có 6 mặt bằng nhau;

C. Có 8 đường chéo;

D. Tất cả các mặt là hình vuông.

Câu 12. Một cái bể dạng hình hộp chữ nhật có chiều dài 1,8 m và chiều rộng bằng chiều dài. Hỏi người ta phải đổ vào trong bể (chưa có nước) đó bao nhiêu lít nước để lượng nước trong bể cao 0,5 m?

A. 720 l;

B. 740 l;

C. 760 l;

D. 780 l.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (2,0 điểm) Cho hai đa thức:

P(x) = x²(2x³ – 3) + 5x⁴ – 7x³ + x² – x;

Q(x) = 3x⁴ – 2x²(x³ – 3) – 2x³ + x² – 1.

a) Thu gọn và sắp xếp mỗi đa thức trên theo lũy thừa giảm dần của biến.

b) Tìm đa thức R(x) biết P(x) = Q(x) + R(x). Xác định bậc, hệ số cao nhất và hệ số tự do của đa thức R(x).

c) Chứng tỏ rằng x = 0 là nghiệm của đa thức P(x) nhưng không là nghiệm của đa thức Q(x).

Bài 2. (1,0 điểm) Bạn Nam đi mua vở và nhẩm tính với số tiền hiện có thì chỉ mua được 10 quyển vở loại I hoặc 12 quyển vở loại II hoặc 15 quyển vở loại III. Biết rằng tổng giá trị tiền 1 quyển vở loại I và 2 quyển vở loại III nhiều hơn giá tiền 2 quyển vở loại II là 4 000 đồng. Tính giá tiền quyển vở loại III.

Bài 3. (1,0 điểm) Gieo ngẫu nhiên con xúc xắc 6 mặt cân đối một lần. Xét các biến cố:

A: “Số chấm xuất hiện trên con xúc xắc là số có một chữ số”;

B: “Số chấm xuất hiện trên con xúc xắc là số chẵn”;

C: “Số chấm xuất hiện trên con xúc xắc chia hết cho 9”.

a) Trong các biến cố trên, biến cố nào là biến cố chắc chắn, biến cố không thể, biến cố ngẫu nhiên?

b) Tính xác suất của biến cố ngẫu nhiên được xác định ở câu a.

Bài 4. (2,5 điểm) Cho ∆ABC cân tại A có hai đường trung tuyến BD và CE cắt nhau tại G.

a) Chứng minh ∆ADB và ∆AEC.

b) Chứng minh DGBC là tam giác cân.

c) Chứng minh $G D + G E > \frac{1}{2} B C$ .

Bài 5. (0,5 điểm) Tìm giá trị nguyên của x để đa thức 3x³+ 10x² – 5 chia hết cho đa thức 3x + 1.

Đáp án đề thi Học kì 2 môn Toán lớp 7 Kết nối tri thức – Đề số 5

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Bảng đáp án:

Câu	1	2	3	4	5	6	7	8	9	10	11	12
Đáp án	A	B	D	D	C	B	C	B	A	D	C	D

Hướng dẫn giải phần trắc nghiệm

Câu 1.

Đáp án đúng là: A

Từ đẳng thức $\frac{4}{- 5, 12} = \frac{2, 5}{- 3, 2}$ lập được tỉ lệ thức:

$\frac{- 3, 2}{- 5, 12} = \frac{2, 5}{4}; \frac{- 3, 2}{2, 5} = \frac{- 5, 12}{4}; \frac{4}{2, 5} = \frac{- 5, 12}{- 3, 2}$ .

Câu 2.

Đáp án đúng là: B

Từ tỉ lệ thức $\frac{2 x + 3}{24} = \frac{3 x - 1}{32}$ ta có $\frac{2 x + 3}{3} = \frac{3 x - 1}{4}$ , suy ra:

3.(3x – 1) = 4.(2x + 3)

9x – 3 = 8x +12

x = 15.

Câu 3.

Đáp án đúng là: D

Phương án D sai vì hệ số tỉ lệ k ≠ 0.

Vậy ta chọn phương án D.

Câu 4.

Đáp án đúng là: D

Biểu thức 16.(3² + 4) là biểu thức số, các biểu thức còn lại chứa chữ nên không là biểu thức số.

Câu 5.

Đáp án đúng là: C

Thay x = –1; y = 2 vào biểu thức C ta có:

C = –2² + 3(–1)³ + 10 = –4 – 3 + 10 = 3.

Câu 6.

Đáp án đúng là: B

Vì 14 ≠ 0 nên đa thức 14 có bậc là 0.

Câu 7.

Đáp án đúng là: C

⦁ Biến cố có khả năng xảy ra cao hơn sẽ có xác suất lớn hơn. Do đó phát biểu (I) đúng.

⦁ Khi tất cả các kết quả của một trò chơi hay phép thử nghiệm ngẫu nhiên đều có khả năng xảy ra bằng nhau thì xác suất xảy ra của mỗi kết quả đều là $\frac{1}{n}$ , trong đó n là số các kết quả. Do đó phát biểu (II) đúng.

Vậy ta chọn phương án C.

Câu 8.

Đáp án đúng là: B

Ta có $\hat{A}; \hat{B}; \hat{C}$ lần lượt là các góc đối diện của các cạnh BC; AC; AB.

Mà AB < BC < AC (do 5 cm < 9 cm < 13 cm).

Suy ra $\hat{C} < \hat{A} < \hat{B}$ (quan hệ giữa cạnh và góc trong một tam giác).

Vậy các góc của ∆ABC sắp xếp theo thứ tự giảm dần là: $\hat{B}; \hat{A}; \hat{C}$ .

Câu 9.

Đáp án đúng là: A

• Xét phương án A có bộ ba độ dài: 2 cm, 5 cm, 7 cm

Ta có: 2 + 5 = 7 không thỏa mãn bất đẳng thức tam giác.

Do đó bộ ba độ dài 2 cm, 5 cm, 7 cm không thể là độ dài ba cạnh của một tam giác.

• Xét phương án B có bộ ba độ dài: 3 cm, 5 cm, 7 cm

Ta có: 3 + 5 > 7 thỏa mãn bất đẳng thức tam giác.

Do đó bộ ba độ dài 3 cm, 5 cm, 7 cm có thể là độ dài ba cạnh của một tam giác.

Tương tự, các bộ ba độ dài ở phương án C, D đều có thể là độ dài ba cạnh của một tam giác.

Vậy ta chọn phương án A.

Câu 10.

Đáp án đúng là: D

Trong một tam giác, trực tâm là giao điểm của ba đường cao.

Câu 11.

Đáp án đúng là: C

Hình lập phương có 4 đường chéo, 12 cạnh bằng nhau, 6 mặt đều là hình vuông và bằng nhau.

Câu 12.

Đáp án đúng là: D

Chiều rộng của hình hộp chữ nhật đó là: 1,8 . $\frac{4}{9}$ = 0,8 (m).

Để lượng nước trong bể cao 0,5 m thì lượng nước trong bể nước là:

1,8 . 0,8 . 0,5 = 0,72 (m³) = 720 (l).

PHẦN II. TỰ LUẬN (7,0 điểm)

Hướng dẫn giải phần tự luận

Bài 1. (2,0 điểm)

a) P(x) = x²(2x³ – 3) + 5x⁴ – 7x³ + x² – x;

= 2x⁵ – 3x² + 5x⁴ – 7x³ + x² – x

= 2x⁵ + 5x⁴ – 7x³ – 2x² – x.

Q(x) = 3x⁴ – 2x²(x³ – 3) – 2x³ + x² – 1

= 3x⁴ – 2x⁵ + 6x² – 2x³ + x² – 1

= –2x⁵ + 3x⁴ – 2x³ + 7x² – 1.

b) Ta có P(x) = Q(x) + R(x)

Suy ra R(x) = P(x) – Q(x)

R(x) = (2x⁵ – 3x² + 5x⁴ – 7x³ + x² – x) – (3x⁴ – 2x⁵ + 6x² – 2x³ + x² – 1)

= 2x⁵ – 3x² + 5x⁴ – 7x³ + x² – x – 3x⁴ + 2x⁵ – 6x² + 2x³ – x² + 1

= 4x⁵ + 2x⁴ – 5x³ – 9x² – x + 1.

Đa thức R(x) có bậc là 5, hệ số cao nhất là 4, hệ số tự do là 1.

c) Ta có P(x) = 2x⁵ + 5x⁴ – 7x³ – 2x² – x có hệ số tự do là 0 nên x = 0 là một nghiệm của đa thức.

Q(0) = –2.0⁵ + 3.0⁴ – 2.0³ + 7.0² – 1 = – 1.

Do đó x = 0 không là nghiệm của đa thức Q(x).

Bài 2. (1,0 điểm)

Gọi x, y, z (đồng) lần lượt là giá tiền của quyển vở loại I, II, III (x, y, z > 0).

Theo bài, tổng giá trị tiền 1 quyển vở loại I và 2 quyển vở loại III nhiều hơn giá tiền 2 quyển vở loại II là 2000 đồng.

Ta suy ra 1 . x + 2 . z – 2 . y = 2 000 hay x – 2y + 2z = 4 000.

Vì số tiền hiện có của bạn Nam không đổi nên số lượng mỗi loại quyển vở mà bạn Nam mua được tỉ lệ nghịch với giá tiền của loại quyển vở đó.

Mà theo bài bạn Nam chỉ mua được 10 quyển vở loại I hoặc 12 quyển vở loại II hoặc 15 quyển vở loại III nên ta có 10x = 12y = 15z.

Suy ra $\frac{10 x}{60} = \frac{12 y}{60} = \frac{15 z}{60}$ hay $\frac{x}{6} = \frac{y}{5} = \frac{z}{4}$ .

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

$\frac{x}{6} = \frac{y}{5} = \frac{z}{4} = \frac{x}{6} = \frac{2 y}{10} = \frac{2 z}{8} = \frac{x + 2 z - 2 y}{6 + 8 - 10} = \frac{4 000}{4} = 1 000$ .

Suy ra: = 1 000 do đó z = 1 000 . 4 = 4 000.

Vậy giá tiền quyển vở loại III là 4 000 đồng.

Bài 3. (1,0 điểm)

a) Biến cố A là biến cố chắc chắn.

Biến cố B là biến cố ngẫu nhiên;

Biến cố C là biến cố không thể.

b) Xác suất của biến cố B là $\frac{1}{2}$ .

Bài 4. (2,5 điểm)

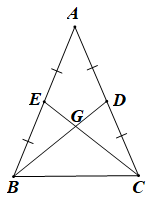
Bộ 30 đề thi Học kì 2 Toán lớp 7 Kết nối tri thức có đáp án (ảnh 1)

a) D là trung điểm AC nên AD = $\frac{1}{2}$ AC

E là trung điểm AB nên AE = $\frac{1}{2}$ AB.

∆ABC cân tại A nên AB = AC.

Suy ra AE = AD.

Xét ∆ADB và ∆AEC, có:

AB = AC (chứng minh trên);

$\hat{B A C}$ là góc chung;

AE = AD (chứng minh trên).

Do đó ∆ADB = ∆AEC (c.g.c).

b) G là trọng tâm của ∆ABC nên $B G = \frac{2}{3} B D$ và $C G = \frac{2}{3} C E$ .

Mà BD = CE (do ∆ADB = ∆AEC)

Nên BG = CG

Do đó ∆GBC cân tại G.

c) G là trọng tâm tam giác ABC nên $G D = \frac{1}{2} G B, G E = \frac{1}{2} G C$

Do đó $G D + G E = \frac{1}{2} (G B + G C)$ .

Mặt khác: BG + CG > BC (bất đẳng thức trong tam giác GCB).

Suy ra $G D + G E > \frac{1}{2} B C$ .

Bài 5. (0,5 điểm)

Thực hiện phép chia đa thức như sau:

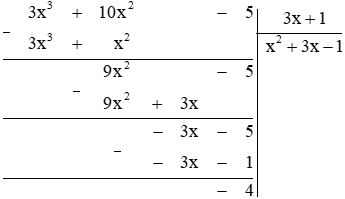
Bộ 30 đề thi Học kì 2 Toán lớp 7 Kết nối tri thức có đáp án (ảnh 1)

Khi đó ta có $\frac{3 x^{3} + 10 x^{2} - 5}{3 x + 1} = x^{2} + 3 x - 1 + \frac{- 4}{3 x + 1}$ .

Để đa thức 3x³+ 10x² – 5 chia hết cho đa thức 3x + 1 thì $\frac{- 4}{3 x + 1}$ phải là số nguyên.

Suy ra – 4 ⋮ (3x + 1) hay (3x + 1) ∈ Ư(– 4) = {– 4; – 1; 1; 4}.

Ta có bảng sau:

3x + 1

– 4

– 1

(nguyên)

(loại)

(chọn)

Khi đó với n ∈ {0; 1} thì đa thức 3x³+ 10x² – 5 chia hết cho đa thức 3x + 1.

Vậy có 2 giá trị x thỏa mãn yêu cầu đề bài.

Bài liên quan:

Leave a Comment Hủy