Sách bài tập Toán 10 Bài 10 (Kết nối tri thức): Vectơ trong mặt phẳng tọa độ

Giải SBT Toán lớp 10 Bài 10: Vectơ trong mặt phẳng tọa độ

Giải SBT Toán 10 trang 58 Tập 1

Bài 4.22 trang 58 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm M(4; 0), N(5; 2) và P(2, 3). Tìm toạ độ các đỉnh của tam giác ABC, biết M, N, P theo thứ tự là trung điểm cạnh BC, CA, AB.

Lời giải:

Cách 1:

Gọi A(x_A; y_A); B(x_B; y_B) và C(x_C; y_C) là tọa độ ba đỉnh của tam giác ABC.

Ta có:

+) M(4; 0) là trung điểm của BC nên $\left\{\begin{array}{l}4=\frac{x_B+x_C}{2}\\ 0=\frac{y_B+y_C}{2}\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}{x}_B+x_C=8\\ y_B+y_C=0\end{array}\right.$                                 (1)

+) N(5; 2) là trung điểm của CA nên $\left\{\begin{array}{l}5=\frac{x_A+x_C}{2}\\ 2=\frac{y_A+y_C}{2}\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}{x}_A+x_C=10\\ y_A+y_C=4\end{array}\right.\iff \left\{\begin{array}{l}{x}_C=10-x_A\\ y_C=4-y_A\end{array}\right.$     (2)

+) P(2; 3) là trung điểm của AB nên $\left\{\begin{array}{l}2=\frac{x_A+x_B}{2}\\ 3=\frac{y_A+y_B}{2}\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}{x}_A+x_B=4\\ y_A+y_B=6\end{array}\right.\iff \left\{\begin{array}{l}{x}_B=4-x_A\\ y_B=6-y_A\end{array}\right.$        (3)

Thay (2) và (3) vào (1) ta được:

$\left\{\begin{array}{l}\left(4-x_A\right)+\left(10-x_A\right)=8\\ \left(6-y_A\right)+\left(4-y_A\right)=0\end{array}\right.$$\iff \left\{\begin{array}{l}14-2x_A=8\\ 10-2y_A=0\end{array}\right.$

$\iff \left\{\begin{array}{l}{x}_A=3\\ y_A=5\end{array}\right.$ Þ A(3; 5)

Khi đó $\left\{\begin{array}{l}{x}_B=4-3=1\\ y_B=6-5=1\end{array}\right.$ Þ B(1; 1)

$\left\{\begin{array}{l}{x}_C=10-3=7\\ y_C=4-5=-1\end{array}\right.$Þ C(7; –1)

Vậy A(3; 5), B(1; 1) và C(7; –1).

Cách 2:

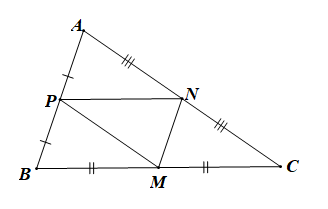
Do M, N, P lần lượt là trung điểm của BC, CA, AB

Nên MN, NP, PM là các đường trung bình của tam giác ABC.

Þ MN // AB, NP // BC, MP // AC.

+) Do MN // BM và NP // BM nên tứ giác MNPB là hình bình hành

$\Rightarrow \overrightarrow{MB}=\overrightarrow{NP}$

Gọi B(x_B; y_B) và có M(4; 0), N(5; 2) và P(2, 3).

$\Rightarrow \overrightarrow{MB}=\left(x_B-4;y_B\right)$ và $\overrightarrow{NP}=\left(2-5;3-2\right)=\left(-3;1\right)$

Khi đó $\overrightarrow{MB}=\overrightarrow{NP}\iff \left\{\begin{array}{l}{x}_B-4=-3\\ y_B=1\end{array}\right.$$\iff \left\{\begin{array}{l}{x}_B=1\\ y_B=1\end{array}\right.$ Þ B(1; 1)

Tương tự ta cũng có A(3; 5) và C(7; –1).

Vậy A(3; 5), B(1; 1) và C(7; –1).

Bài 4.23 trang 58 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(2;–1), B(1; 4) và C(7; 0).

a) Tính độ dài các đoạn thẳng AB, BC và CA. Từ đó suy ra tam giác ABC là một tam giác vuông cân.

b) Tìm toạ độ của điểm D sao cho tứ giác ABDC là một hình vuông.

Lời giải:

a) Với A(2;–1), B(1; 4) và C(7; 0) ta có:

 

 

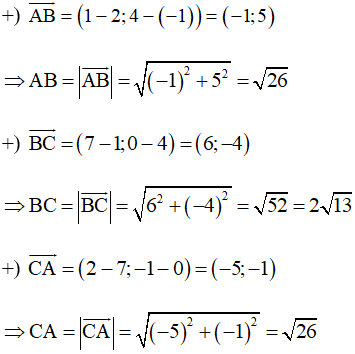
Do đó AB = CA $\left(=\sqrt{26}\right)$

Nên tam giác ABC cân tại A               (1)

Mặt khác: $B{C}^2={\left(2\sqrt{13}\right)}^2=52$

Và $A{B}^2+A{C}^2={\left(\sqrt{26}\right)}^2+{\left(\sqrt{26}\right)}^2=52$

Þ BC² = AB² + AC²

Theo định lí Pythagoras đảo thì tam giác ABC vuông tại A        (2)

Từ (1) và (2) suy ra tam giác ABC vuông cân tại A với $AB=AC=\sqrt{26};BC=2\sqrt{13}.$

b)

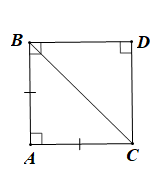
Vì ABC là tam giác vuông cân

Nên để ABDC là hình vuông thì tứ giác ABDC là hình bình hành

$\iff \overrightarrow{CA}=\overrightarrow{DB}$

Gọi D(x_D; y_D) và có A(2;–1), B(1; 4), C(7; 0).

$\Rightarrow \overrightarrow{CA}=\left(-5;-1\right)$và $\overrightarrow{DB}=\left(1-x_D;4-y_D\right)$

Do đó $\overrightarrow{CA}=\overrightarrow{DB}\iff \left\{\begin{array}{l}-5=1-x_D\\ -1=4-y_D\end{array}\right.$

$\iff \left\{\begin{array}{l}{x}_D=6\\ y_D=5\end{array}\right.$ Þ D(6; 5).

Vậy tọa độ điểm D cần tìm là D(6; 5).

Bài 4.24 trang 58 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho hai điểm M(–2; 1) và N(4; 5).

a) Tìm toạ độ của điểm P thuộc Ox sao cho PM = PN.

b) Tìm toạ độ của điểm Q sao cho $\overrightarrow{MQ}=2\overrightarrow{PN}.$

c) Tìm toạ độ của điểm R thoả mãn $\overrightarrow{RM}+2\overrightarrow{RN}=\overrightarrow{0}.$ Từ đó suy ra P, Q, R thẳng hàng.

Lời giải:

a) Gọi P(a; 0) là điểm thuộc tia Ox.

Với M(–2; 1) và N(4; 5) ta có:

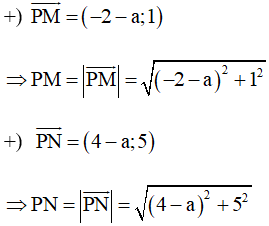
 Do đó PM = PN $\iff \sqrt{{\left(-2-a\right)}^2+1^2}=\sqrt{{\left(4-a\right)}^2+5^2}$

Û (–2 – a)² + 1² = (4 – a)² + 5²

Û 4 + 4a + a² + 1 = 16 – 8a + a² + 25

Û 12a = 36

Û a = 3.

Vậy P(3; 0).

b) Giả sử điểm Q có tọa độ là Q(x; y).

Với M(–2; 1), N(4; 5) và P(3; 0) ta có:

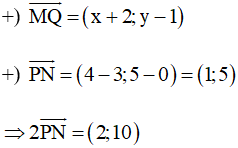
Do đó $\overrightarrow{MQ}=2\overrightarrow{PN}\iff \left\{\begin{array}{l}x+2=2\\ y-1=10\end{array}\right.$

$\iff \left\{\begin{array}{l}x=0\\ y=11\end{array}\right.$ Þ Q(0; 11).

Vậy Q(0; 11).

c) Giả sử R(x₀; y₀) là điểm cần tìm.

Với M(–2; 1) và N(4; 5) ta có:

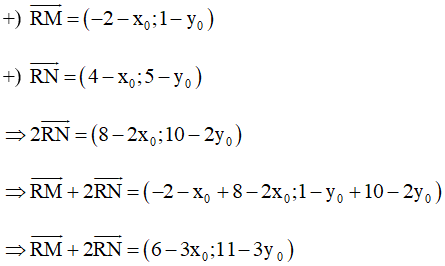
Do đó 

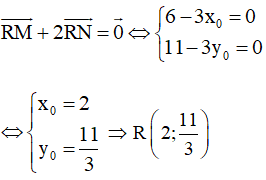
+) Ta xét ba điểm: P(3; 0), Q(0; 11) và $R\left(2;\frac{11}{3}\right)$

$\Rightarrow \overrightarrow{PQ}=\left(-3;11\right)$và $\overrightarrow{QR}=\left(2;\frac{11}{3}-11\right)=\left(2;\frac{-22}{3}\right)$

Có: $\frac{-3}{2}=\frac{11}{\frac{-22}{3}}$ nên hai vectơ $\overrightarrow{PQ}$ và $\overrightarrow{QR}$ cùng phương

Do đó P, Q, R thẳng hàng

Vậy ba điểm P, Q, R thẳng hàng.

Giải SBT Toán 10 trang 59, 60 Tập 1

Bài 4.25 trang 59 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho hai điểm M(–3; 2) và N(2; 7).

a) Tìm toạ độ của điểm P thuộc trục tung sao cho M, N, P thẳng hàng.

b) Tìm toạ độ của điểm Q đối xứng với N qua Oy.

c) Tìm toạ độ của điểm R đối xứng với M qua trục hoành.

Lời giải:

a) Giả sử P(0; y_P) là điểm thuộc trục tung.

Với M(–3; 2) và N(2; 7) ta có:

$\overrightarrow{MP}=\left(3;y_P-2\right)$ và $\overrightarrow{NP}=\left(-2;y_P-7\right)$

Ba điểm M, N, P thẳng hàng

$\iff \overrightarrow{MP}$ và $\overrightarrow{NP}$ cùng phương

$\iff \frac{3}{-2}=\frac{y_P-2}{y_P-7}$ (với y_P ≠ 7)

Û 3.(y_P – 7) = –2.(y_P – 2)

Û 3.y_P – 21 = –2y_P + 4

Û 3.y_P + 2y_P = 4 + 21

Û 5.y_P = 25

Û y_P = 5 (thỏa mãn)

Vậy P(0; 5).

b)

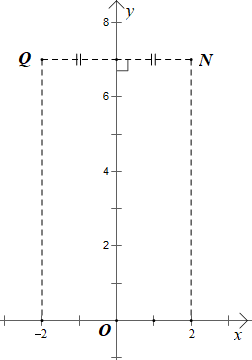
Vì Q đối xứng với N(2; 7) qua Oy nên:

+ Hoành độ của điểm Q là số đối của hoành độ điểm N;

+ Tung độ của điểm Q bằng với tung độ của điểm N.

Do đó Q(–2; 7).

Vậy Q(–2; 7).

c)

Vì R đối xứng với M(–3; 2) qua trục hoành nên:

+ Hoành độ của điểm R bằng hoành độ điểm M;

+ Tung độ của điểm R bằng số đối của tung độ điểm M.

Do đó R(–3; –2).

Vậy R(–3; –2).

Bài 4.26 trang 60 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho hai điểm C(1; 6) và D(11; 2).

a) Tìm toạ độ của điểm E thuộc trục tung sao cho vectơ $\overrightarrow{EC}+\overrightarrow{ED}$ có độ dài ngắn nhất.

b) Tìm toạ độ của điểm F thuộc trục hoành sao cho $\left|2\overrightarrow{FC}+3\overrightarrow{FD}\right|$ đạt giá trị nhỏ nhất.

c) Tìm tập hợp các điểm M sao cho $\left|\overrightarrow{MC}+\overrightarrow{MD}\right|=CD.$

Lời giải:

a) Giả sử E(0; y_E) là điểm thuộc trục tung.

Với C(1; 6) và D(11; 2) ta có:

$\overrightarrow{EC}=\left(1;6-y_E\right)$ và $\overrightarrow{ED}=\left(11;2-y_E\right)$

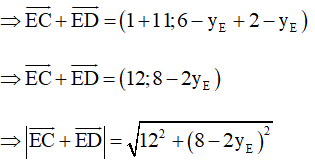
Vì (8 – 2y_E)² ≥ 0 ∀ y_E

Nên 12² + (8 – 2y_E)² ≥ 12² ∀ y_E

Hay $\sqrt{{12}^2+{\left(8-2y_E\right)}^2}\ge 12$ ∀ y_E

$\Rightarrow \left|\overrightarrow{EC}+\overrightarrow{ED}\right|\ge 12$ ∀ y_E

Do đó độ dài của vectơ $\overrightarrow{EC}+\overrightarrow{ED}$ nhỏ nhất bằng 12

Dấu “=’ xảy ra Û 8 – 2y_E = 0

Û y_E = 4

Vậy với E(0; 4) thì vectơ $\overrightarrow{EC}+\overrightarrow{ED}$ có độ dài ngắn nhất.

b) Giả sử F(a; 0) thuộc trục hoành.

Với C(1; 6) và D(11; 2) ta có:

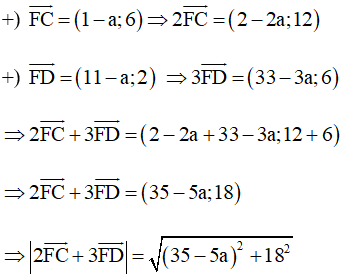
Vì (35 – 5a)² ≥ 0 ∀a

Nên (35 – 5a)² + 18² ≥ 18² ∀a

Hay $\sqrt{{\left(35-5a\right)}^2+{18}^2}$ ∀a

$\Rightarrow \left|2\overrightarrow{FC}+3\overrightarrow{FD}\right|\ge 18$ ∀a

Do đó độ dài của vectơ $2\overrightarrow{FC}+3\overrightarrow{FD}$ nhỏ nhất bằng 18

Dấu “=’ xảy ra Û 35 – 5a = 0

Û a = 7

Vậy với F(7; 0) thì $\left|2\overrightarrow{FC}+3\overrightarrow{FD}\right|$ đạt giá trị nhỏ nhất.

c) Giả sử M(x ; y) là tọa độ điểm thỏa mãn $\left|\overrightarrow{MC}+\overrightarrow{MD}\right|=CD.$

Với C(1; 6) và D(11; 2) ta có:

+) $\overrightarrow{CD}=\left(10;-4\right)$

$\Rightarrow CD=\left|\overrightarrow{CD}\right|=\sqrt{{10}^2+{\left(-4\right)}^2}$$=\sqrt{116}=2\sqrt{29}$

Gọi I là trung điểm của CD, khi đó ta có:

• Tọa độ của I là: $\left\{\begin{array}{l}{x}_I=\frac{1+11}{2}=6\\ y_I=\frac{6+2}{2}=4\end{array}\right.$ Þ I(6; 4).

• $\overrightarrow{MC}+\overrightarrow{MD}=2\overrightarrow{MI}$

$\Rightarrow \left|\overrightarrow{MC}+\overrightarrow{MD}\right|=\left|2\overrightarrow{MI}\right|=2.MI$

Ta có

$\left|\overrightarrow{MC}+\overrightarrow{MD}\right|=CD\iff 2MI=CD$

$\iff IM=\frac{CD}{2}=\frac{2\sqrt{29}}{2}=\sqrt{29}.$

Do đó tập hợp điểm M là đường tròn tâm I(6; 4) và bán kính $R=\sqrt{29}.$

Giải SBT Toán 10 trang 61, 62 Tập 1

Bài 4.27 trang 61 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(1; 2), B(3; 4) và C(2; –1).

a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác. Tìm toạ độ trọng tâm của tam giác đó.

b) Tìm toạ độ tâm I của đường tròn ngoại tiếp và trực tâm H của tam giác ABC.

Lời giải:

a) Với ba điểm A(1; 2), B(3; 4) và C(2; –1) ta có:

+) $\overrightarrow{AB}=\left(2;2\right)$

+) $\overrightarrow{AC}=\left(1;-3\right)$

Do $\frac{2}{1}\ne \frac{2}{-3}$ nên hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ không cùng phương

Do đó ba điểm A, B, C không thẳng hàng nên tạo thành một tam giác.

Gọi G(x; y) là tọa độ trọng tâm của tam giác ABC

$\Rightarrow \left\{\begin{array}{l}x=\frac{1+3+2}{3}=2\\ y=\frac{2+4+\left(-1\right)}{3}=\frac{5}{3}\end{array}\right.$ $\Rightarrow G\left(2;\frac{5}{3}\right)$

Vậy $\Rightarrow G\left(2;\frac{5}{3}\right)$

b) * Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.

Gọi I(a; b) là tọa độ tâm đường tròn ngoại tiếp tam giác ABC.

Khi đó IA = IB = IC.

Với ba điểm A(1; 2), B(3; 4) và C(2; –1) ta có:

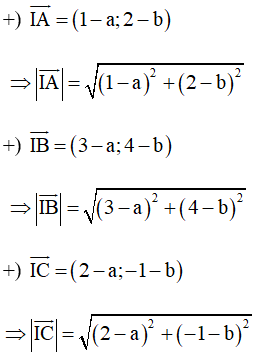
Do đó IA = IB = IC Û IA² = IB² = IC²

Û (1 – a)² + (2 – b)² = (3 – a)² + (4 – b)² = (2 – a)² + (–1 – b)²

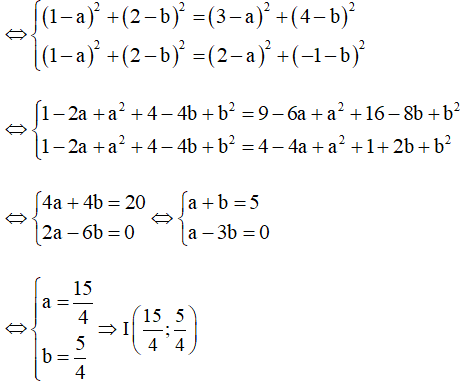
* Tìm tọa độ trực tâm H của tam giác ABC.

Gọi H(x₀; y₀) là tọa độ trực tâm của tam giác ABC.

Vì H là trực tâm của tam giác ABC nên theo kết quả của Bài 4.15, phần a) trang 54 ta có $\overrightarrow{AH}=2\overrightarrow{IM}$ (với M là trung điểm của BC).

Với A(1; 2), B(3; 4), C(2; –1) và $I\left(\frac{15}{4};\frac{5}{4}\right)$ ta có:

• Trung điểm M của BC có tọa độ là:  

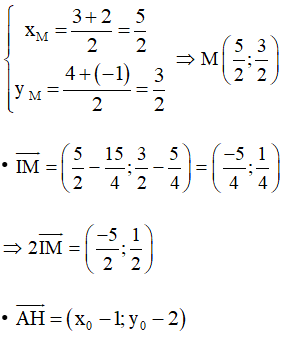
Ta có: 

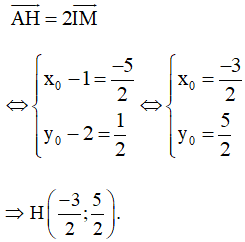
Vậy $I\left(\frac{15}{4};\frac{5}{4}\right)$ và $H\left(\frac{-3}{2};\frac{5}{2}\right).$

Bài 4.28 trang 62 SBT Toán 10 Tập 1: Để kéo đường dây điện băng qua một hồ hình chữ nhật ABCD với độ dài AB = 200 m, AD = 180 m, người ta dự định làm 4 cột điện liên tiếp cách đều, cột thứ nhất nằm trên bờ AB và cách đỉnh A khoảng cách 20 m, cột thứ tư nằm trên bờ CD và cách đỉnh C khoảng cách 30 m. Tính các khoảng cách từ vị trí các cột thứ hai, thứ ba đến các bờ AB, AD.

Lời giải:

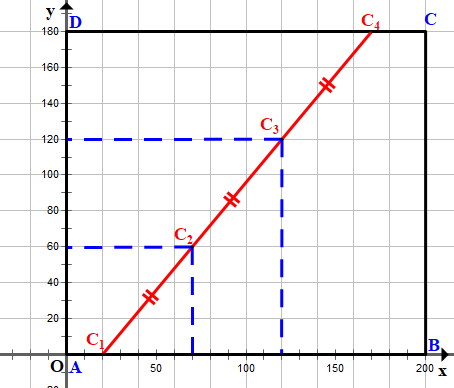
Chọn hệ trục tọa độ Oxy sao cho các đỉnh của hình hồ hình chữ nhật có các tọa độ là A(0; 0), B(200; 0), C(200; 180) và D(0; 180).

Gọi vị trí các cột điện được trồng là C₁, C₂, C₃ và C₄.

Vì vị trí cột điện thứ nhất C₁ nằm trên bờ AB và cách A một khoảng 20 m nên trong hệ trục tọa độ đã chọn, điểm C₁(20; 0).

Vị trí cột điện thứ tư nằm trên bờ CD và cách C một khoảng 30 m nên khoảng cách từ C₄ đến D là 170 m. Khi đó trong hệ trục tọa độ đã chọn, điểm C₄(170; 180).

Vì bốn cột điện được trồng liên tiếp nhau và cách đều trên một đường thẳng nên:

C₁C₂ = C₂C₃ = C₃C₄

Þ C₁C₂ = $\frac{1}{3}$C₁C₄ và C₁C₃ = $\frac{2}{3}$C₁C₄.

$\Rightarrow \overrightarrow{C_1{C}_2}=\frac{1}{3}\overrightarrow{C_1{C}_4}$ và $\overrightarrow{C_1{C}_3}=\frac{2}{3}\overrightarrow{C_1{C}_4}$

Giả sử C₂(a; b) và C₃(x; y).

Với C₁(20; 0), C₄(170; 180) ta có:

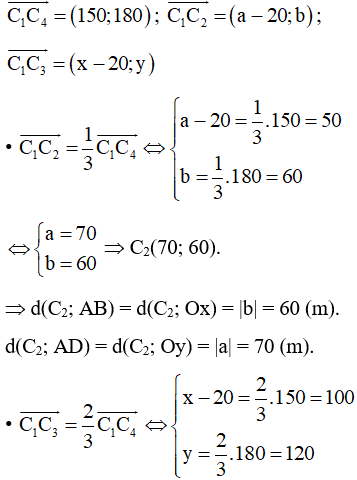
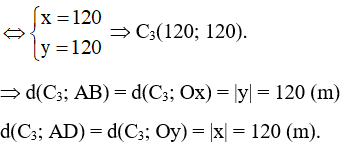
Vậy khoảng cách từ cột điện thứ hai đến bờ AB là 60 m và đến bờ AD là 70 m.

Khoảng cách từ cột điện thứ ba đến bờ AB là 120 m và đến bờ AD là 120 m.

Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 9: Tích của một vectơ với một số

Bài 11: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Bài 12: Số gần đúng và sai số

====== ****&**** =====