Câu hỏi:
Dãy các số hữu tỉ được sắp xếp theo chiều tăng dần là
A. \(\frac{{ – 1}}{9}\), \(\frac{{ – 5}}{{27}}\), \(\frac{7}{{25}}\), \(\frac{8}{{125}}\);
B. \(\frac{7}{{25}}\), \(\frac{8}{{125}}\), \(\frac{{ – 1}}{9}\), \(\frac{{ – 5}}{{27}}\);
C. \(\frac{{ – 5}}{{27}}\), \(\frac{{ – 1}}{9}\), \(\frac{8}{{125}}\), \(\frac{7}{{25}}\);
Đáp án chính xác
D. \(\frac{8}{{125}}\), \(\frac{7}{{25}}\), \(\frac{{ – 1}}{9}\), \(\frac{{ – 5}}{{27}}\);
Trả lời:
Đáp án đúng là: C
Ta có: \(\frac{{ – 1}}{9} = \frac{{ – 3}}{{27}}\) mà \(\frac{{ – 3}}{{27}}\) > \(\frac{{ – 5}}{{27}}\) > 0 nên \(\frac{{ – 1}}{9}\) > \(\frac{{ – 5}}{{27}}\) > 0
\(\frac{7}{{25}}\) = \(\frac{{35}}{{125}}\) mà \(\frac{{35}}{{125}}\) > \(\frac{8}{{125}}\) > 0 nên \(\frac{7}{{25}}\) > \(\frac{8}{{125}}\) > 0
Do đó: \(\frac{{ – 5}}{{27}}\) < \(\frac{{ – 1}}{9}\) < \(\frac{8}{{125}}\) < \(\frac{7}{{25}}\).
</>
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập hợp số hữu tỉ được kí hiệu là
Câu hỏi:
Tập hợp số hữu tỉ được kí hiệu là
A. ℕ;
B. ℤ;
C. ℚ;
Đáp án chính xác
D. ℝ.
Trả lời:
Đáp án đúng là: C
Tập hợp số hữu tỉ được kí hiệu là ℚ.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số hữu tỉ được viết dưới dạng
Câu hỏi:
Số hữu tỉ được viết dưới dạng
A. \(\frac{a}{b}\) với a, b ∈ ℤ, b ≠ 0;
A. \(\frac{a}{b}\) với a, b ∈ ℤ, b ≠ 0;
A. \(\frac{a}{b}\) với a, b ∈ ℤ, b ≠ 0;
Đáp án chính xác
A. \(\frac{a}{b}\) với a, b ∈ ℤ, b ≠ 0;
Trả lời:
Đáp án đúng là: C
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}\) với a, b ∈ ℤ, b ≠ 0.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số không phải số hữu tỉ là
Câu hỏi:
Số không phải số hữu tỉ là
A. \(\frac{{ – 1}}{2}\);
B. \(3\frac{5}{8}\);
C. 1,5;
D. \(\frac{3}{0}\).
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
Số hữu tỉ được viết dưới dạng \(\frac{a}{b}\) với a, b ∈ ℤ, b ≠ 0. Nên \(\frac{{ – 1}}{2}\) là số hữu tỉ.
Các số \(3\frac{5}{8}\); 1,5 cũng là số hữu tỉ vì đều viết được dưới dạng \[\frac{a}{b}\] với a, b ∈ ℤ, b ≠ 0;
\(3\frac{5}{8}\) = \(\frac{{29}}{8}\); 1,5 = \(\frac{3}{2}\).
\(\frac{3}{0}\) không là số hữu tỉ vì có mẫu số bằng 0.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Các điểm B, C lần lượt biểu diễn những số hữu tỉ nào?
Câu hỏi:
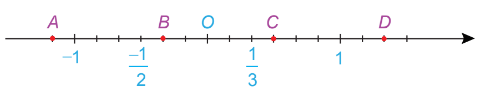
Các điểm B, C lần lượt biểu diễn những số hữu tỉ nào?
A. \(\frac{1}{3}\), \(\frac{1}{2}\);
B. \(\frac{{ – 1}}{3}\), \(\frac{1}{4}\);
C. \(\frac{{ – 1}}{3}\), \(\frac{1}{2}\);
Đáp án chính xác
D. \(\frac{{ – 1}}{3}\), \(\frac{1}{6}\).
Trả lời:
Đáp án đúng là: C
Đoạn thẳng từ điểm O đến 1 được chia thành 6 phần bằng nhau.
Đoạn thẳng OB chiếm 2 phần; B nằm trước O nên biểu diễn số hữu tỉ âm.
Vậy điểm B biểu diễn số hữu tỉ là \(\frac{{ – 2}}{6} = \frac{{ – 1}}{3}\).
Đoạn thẳng OC chiếm 3 phần; C nằm sau O nên biểu diễn số hữu tỉ dương.
Vậy điểm C biểu diễn số hữu tỉ là \(\frac{3}{6} = \frac{1}{2}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số đối của số hữu tỉ \(\frac{7}{2}\) là
Câu hỏi:
Số đối của số hữu tỉ \(\frac{7}{2}\) là
A. \( – \frac{7}{2}\);
Đáp án chính xác
B. \(\frac{2}{7}\);
C. \( – \frac{2}{7}\);
D. 3,5.
Trả lời:
Đáp án đúng là: A
Số đối của số hữu tỉ \(\frac{7}{2}\) là \( – \frac{7}{2}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====