Câu hỏi:
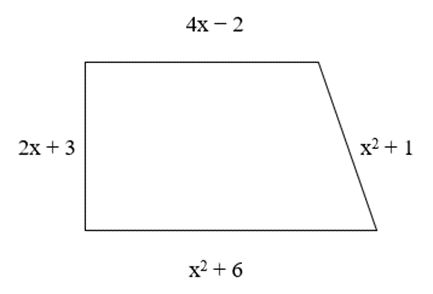
Biểu thức biểu thị chu vi của hình thang vuông như hình bên dưới là:
A. x2 + 6x + 4;
B. 2x2 − 6x + 8;
C. 2x2 + 2x + 8;
D. 2x2 + 6x + 8.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
Chu vi của hình thang bằng tổng độ dài hai cạnh đáy và hai cạnh bên. Khi đó:
P = (4x − 2 + x2 + 6) + (2x + 3 + x2 + 1) (với P là chu vi của hình thang)
= 4x − 2 + x2 + 6 + 2x + 3 + x2 + 1
= (x2 + x2) + (4x + 2x) + (−2 + 6 + 3 + 1)
= 2x2 + 6x + 8.
Vậy chu vi của hình thang vuông trên được biểu thị bằng biểu thức 2x2 + 6x + 8.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hai đa thức G(x) = 2x + 7 và H(x) = 3x + 6. Tính G(x) + H(x).
Câu hỏi:
Cho hai đa thức G(x) = 2x + 7 và H(x) = 3x + 6. Tính G(x) + H(x).
A. −x + 1;
B. 5x + 13;
Đáp án chính xác
C. 5x + 1;
D. x − 1.
Trả lời:
Đáp án đúng là: B
Ta có: G(x) + H(x) = (2x + 7) + (3x + 6)
= 2x + 7 + 3x + 6 = (2x + 3x) + (6 + 7) = 5x + 13.
Vậy G(x) + H(x) = 5x + 13.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hai đa thức A(x) = x2 − 5x + 7 và B(x) = 3×2 − 2x + 10. Tính A(x) + B(x).
Câu hỏi:
Cho hai đa thức A(x) = x2 − 5x + 7 và B(x) = 3x2 − 2x + 10. Tính A(x) + B(x).
A. 3x2 − 2x + 10;
B. 3x2 − 2x + 10;
C. 4x2 − 7x + 17;
Đáp án chính xác
D. −2x2 − 3x + 10.
Trả lời:
Đáp án đúng là: C
Ta có: A(x) + B(x) = (x2 − 5x + 7) + (3x2 − 2x + 10)
= x2 − 5x + 7 + 3x2 − 2x + 10
= (x2 + 3x2) + (−5x − 2x) + (7 + 10)
= 4x2 − 7x + 17.
Vậy A(x) + B(x) = 4x2 − 7x + 17.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hai đa thức P(x) = 6×3 − 3×2 − 2x + 4 và G(x) = 5×2 − 7x + 9. Tính P(x) − G(x).
Câu hỏi:
Cho hai đa thức P(x) = 6x3 − 3x2 − 2x + 4 và G(x) = 5x2 − 7x + 9. Tính P(x) − G(x).
A. x2 − 9x + 13;
B. 6x3 − 8x2 + 5x − 5;
Đáp án chính xác
C. x3 − 8x2 + 5x − 5;
D. 5x3 − 8x2 + 5x + 13.
Trả lời:
Đáp án đúng là: B
Ta có: P(x) − G(x) = (6x3 − 3x2 − 2x + 4) − (5x2 − 7x + 9)
= 6x3 − 3x2 − 2x + 4 − 5x2 + 7x − 9
= 6x3 + (−3x2 − 5x2) + (−2x + 7x) + (4 − 9)
= 6x3 − 8x2 + 5x − 5.
Vậy P(x) − G(x) = 6x3 − 8x2 + 5x −5.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đa thức U(x) = 7×2 + 4x − 3. Tìm đa thức V(x) sao cho U(x) + V(x) = x3 + x2 – 5.
Câu hỏi:
Cho đa thức U(x) = 7x2 + 4x − 3. Tìm đa thức V(x) sao cho U(x) + V(x) = x3 + x2 – 5.
A. V(x) = x3 − 6x2 − 4x − 2;
Đáp án chính xác
B. V(x) = 6x2 − 4x − 2;
C. V(x) = x3 − 8x2 + 5x + 13;
D. V(x) = x3 − 6x2 − 2.
Trả lời:
Đáp án đúng là: A
Ta có: U(x) = 7x2 + 4x − 3
Vì U(x) + V(x) = x3 + x2 −5 nên
V(x) = x3 + x2 − 5 − U(x)
= x3 + x2 − 5 − (7x2 + 4x − 3)
= x3 + x2 − 5 − 7x2 − 4x + 3
= x3 + (x2 − 7x2) − 4x + (−5 + 3)
= x3 − 6x2 − 4x – 2.
Vậy V(x) = x3 − 6x2 − 4x – 2.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đa thức G(x) = 3×4 − 4×3 − 2x + 27. Tìm đa thức H(x) sao cho H(x) − G(x) = x3 − 5×2 + 10.
Câu hỏi:
Cho đa thức G(x) = 3x4 − 4x3 − 2x + 27. Tìm đa thức H(x) sao cho H(x) − G(x) = x3 − 5x2 + 10.
A. 3x4 − 3x3 − 5x2 + 2x + 37;
B. 3x4 + 3x3 − 5x2 − 2x + 37;
C. − 3x3 − 5x2 − 2x + 37;
D. 3x4 − 3x3 − 5x2 − 2x + 37.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
Ta có: G(x) = 3x4 − 4x3 − 2x + 27
Vì H(x) − G(x) = x3 − 5x2 + 10 nên:
H(x) = x3 − 5x2 + 10 + G(x)
= x3 − 5x2 + 10 + (3x4 − 4x3 − 2x + 27)
= x3 − 5x2 + 10 + 3x4 − 4x3 − 2x + 27
= 3x4 + (x3 − 4x3) − 5x2 − 2x + (10 + 27)
= 3x4 − 3x3 − 5x2 − 2x + 37.
Vậy H(x) = 3x4 − 3x3 − 5x2 − 2x + 37.====== **** mời các bạn xem câu tiếp bên dưới **** =====