Câu hỏi:
Cho định lí: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông”. Giả thiết, kết luận của định lí là:
A. Giả thiết: Cho góc bẹt AOB và tia OI; tia OJ là tia phân giác góc BOI, OK là tia phân giác AOI. Kết luận \[OI \bot OK\].
Đáp án chính xác
B. Giả thiết: Cho góc bẹt AOB và tia OI; tia OJ là tia phân giác góc BOK, OK là tia phân giác AOI. Kết luận .\[OI \bot OA\]..
C. Giả thiết: Cho góc bẹt AOB và tia OI; tia OJ là tia phân giác góc BOI, OK là tia phân giác AOK. Kết luận \[OI \bot OK\].
D. Giả thiết: Cho góc bẹt AOB và tia OI; tia OJ là tia phân giác góc BOI, OK là tia phân giác AOI. Kết luận \[OB \bot OK\].
Trả lời:
Đáp án đúng là: A
Giả thiết: Cho góc bẹt AOB và tia OI; tia OJ là tia phân giác góc BOI, OK là tia phân giác AOI. Kết luận \[OI \bot OK\].
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình vẽ. Tính góc FEC, biết EF // BC và \[\widehat {ECB} = 40^\circ \]:
Câu hỏi:
Cho hình vẽ. Tính góc FEC, biết EF // BC và \[\widehat {ECB} = 40^\circ \]:
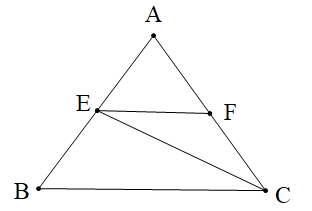
A. 50°;
B. 40°;
Đáp án chính xác
C. 60°;
D. 30°.
Trả lời:
Đáp án đúng là: B
Vì EF // BC nên ta có: \[\widehat {ECB}\] và \[\widehat {FEC}\] là hai góc so le trong
Suy ra \[\widehat {FEC} = \widehat {ECB} = 40^\circ \]
Vậy \[\widehat {FEC} = 40^\circ \].====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình thoi ABCD như hình vẽ.
Chọn phương án đúng.
Câu hỏi:
Cho hình thoi ABCD như hình vẽ.
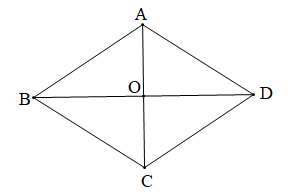
Chọn phương án đúng.A. \[\widehat {AOB}\] và \[\widehat {DOC}\] là hai góc đối đỉnh;
Đáp án chính xác
B. \[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc so le trong;
C. \[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc đồng vị;
D. \[\widehat {ABC}\] và \[\widehat {ADC}\] là hai góc kề bù.
Trả lời:
Đáp án đúng là: A
\[\widehat {AOB}\] và \[\widehat {DOC}\] là hai góc đối đỉnh là phát biểu đúng, chọn phương án A;
\[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc so le trong là phát biểu sai, vì \[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc kề bù;
\[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc đồng vị là phát biểu sai, vì \[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc trong cùng phía.
\[\widehat {ABC}\] và \[\widehat {ADC}\] là hai góc kề bù là phát biểu sai vì hai góc này không chung đỉnh.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình chữ nhật ABCD như hình vẽ. Biết IJ // AB và \[\widehat {JOC} = 30^\circ \].
Số đo góc BAC là:
Câu hỏi:
Cho hình chữ nhật ABCD như hình vẽ. Biết IJ // AB và \[\widehat {JOC} = 30^\circ \].
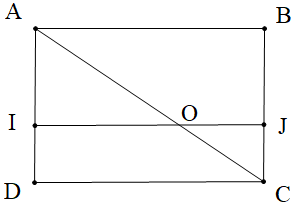
Số đo góc BAC là:A. 60°;
Đáp án chính xác
B. 30°;
C. 90°;
D. 80°.
Trả lời:
Đáp án đúng là: A.
Vì AB // IJ nên ta có: \[\widehat {JOC}\] và \[\widehat {BAC}\] là hai góc đồng vị
Suy ra \[\widehat {BAC} = \widehat {JOC} = 30^\circ \] (1)
Vậy \[\widehat {BAC} = 60^\circ \].====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình bình hành ABCD như hình vẽ. Biết EF // DC, \[\widehat {DAB} = 65^\circ \] và \[\widehat {AFE} = 35^\circ \]. Số đo góc KAD là:
Câu hỏi:
Cho hình bình hành ABCD như hình vẽ. Biết EF // DC, \[\widehat {DAB} = 65^\circ \] và \[\widehat {AFE} = 35^\circ \]. Số đo góc KAD là:
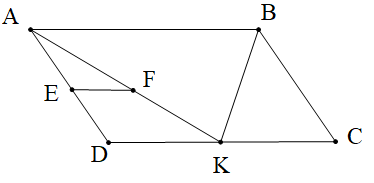
A. 60°;
B. 45°;
C. 30°;
Đáp án chính xác
D. 125°.
Trả lời:
Đáp án đúng là: C
Vì ABCD là hình bình hành nên AB // DC do đó \(\widehat {BAK} = \widehat {AKD}\) (hai góc so le trong).
Vì EF // DC nên \[\widehat {AFE} = \widehat {AKD}\] (hai góc đồng vị)
Suy ra \(\widehat {BAK} = \widehat {AFE}\) (cùng bằng góc \(\widehat {AKD}\))
Mà \[\widehat {AFE} = 35^\circ \Rightarrow \widehat {BAK} = 35^\circ \]
Mà \[\widehat {BAK} + \widehat {KAD} = \widehat {DAB}\] (vì tia AK nằm giữa hai tia AB và AD)
\[ \Rightarrow \widehat {KAD} = \widehat {DAB} – \widehat {KAB} = 65^\circ – 35^\circ = 30^\circ \]
Vậy \[\widehat {KAD} = 30^\circ \].====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình vẽ dưới đây, biết a // b. Tính x, y.
Câu hỏi:
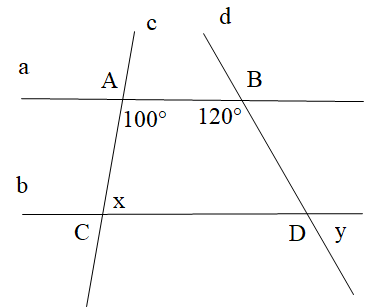
Cho hình vẽ dưới đây, biết a // b. Tính x, y.
A.
x = 80° và y = 80°;B. x = 60° và y = 80°;
Đáp án chính xác
C. x = 80° và y = 60°;
D. x = 60° và y = 60°.
Trả lời:
Đáp án đúng là: B
Vì a // b nên \[\widehat {BAC} + \widehat {ACD} = 180^\circ \] (hai góc trong cùng phía bù nhau)
Suy ra 100o + x = 180o
Do đó x = 180o ‒ 100° = 80°
Vì a // b nên \[\widehat {ABD} + \widehat {CDB} = 180^\circ \] (hai góc trong cùng phía bù nhau)
Suy ra \[\widehat {CDB} = 180^\circ – \widehat {ABD}\]
\[\widehat {CDB} = 180^\circ – 120^\circ = 60^\circ \]
Mà góc y và \(\widehat {CDB}\) là hai góc đổi đỉnh nên \[y = \widehat {CDB} = 60^\circ \]
Vậy x = 80° và y = 60°.====== **** mời các bạn xem câu tiếp bên dưới **** =====