Câu hỏi:
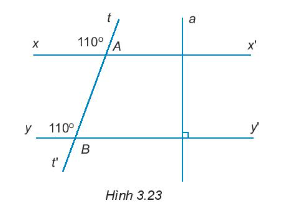
Vẽ lại Hình 3.23 vào vở. Giải thích tại sao
xx’ // yy’.
Trả lời:
Lời giải:
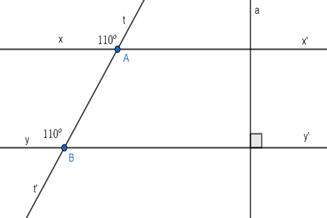
Ta có: \(\widehat {tAx}\) = 110o và \(\widehat {yBt}\) = 110o nên \(\widehat {tAx}\) = \(\widehat {yBt}\) = 110o. Mà hai góc này ở vị trí đồng vị. Do đó, xx’ song song với yy’.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
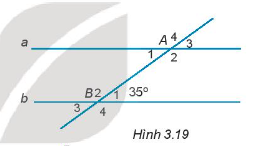
- Cho Hình 3.19, biết a // b.
Tính số đo góc A1.
Câu hỏi:
Cho Hình 3.19, biết a // b.
Tính số đo góc A1.
Trả lời:
Lời giải:
Vì a // b nên \(\widehat {{A_1}}\) và góc \(\widehat {{B_1}}\) là hai góc so le trong.
Do đó, \(\widehat {{A_1}}\) = \(\widehat {{B_1}}\) = 35o.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- So sánh góc A4 và B2.
Câu hỏi:
So sánh góc A4 và B2.
Trả lời:
Hướng dẫn giải:
Vì a // b nên các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.
Ta có, \(\widehat {{A_4}}\) và \(\widehat {{B_2}}\) là hai góc đồng vị.
Do đó, \(\widehat {{A_4}}\) = \(\widehat {{B_2}}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tính số đo góc A2.
Câu hỏi:
Tính số đo góc A2.
Trả lời:
Hướng dẫn giải:
Vì \(\widehat {{A_1}}\) và \(\widehat {{A_2}}\) là hai góc kề bù nên \(\widehat {{A_1}}\) + \(\widehat {{A_2}}\) = 180o
Thay số: 35o + \(\widehat {{A_2}}\) = 180o
\(\widehat {{A_2}}\) = 180o – 35o
\(\widehat {{A_2}}\) = 145o.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Vẽ lại Hình 3.20 vào vở
Câu hỏi:
Vẽ lại Hình 3.20 vào vở
Giải thích tại sao Ax // By.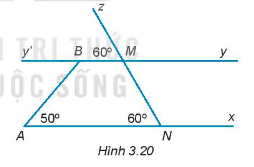
Trả lời:
Lời giải:
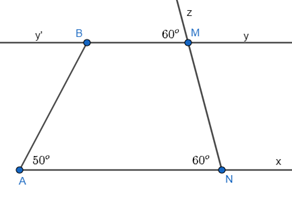
Ta có:
\(\widehat {zMy’} = \widehat {zNA} = 60^\circ \) mà \(\widehat {zMy’}\) và \(\widehat {zNA}\) là hai góc đồng vị.
Do đó, Ax // By.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tính số đo góc ABy’.
Câu hỏi:
Tính số đo góc ABy’.
Trả lời:
Hướng dẫn giải:
Vì Ax // By nên các góc so le trong bằng nhau và các góc đồng vị bằng nhau.
Lại có: \(\widehat {ABy’}\) và \(\widehat {BAx}\) là hai góc so le trong.
Do đó, \(\widehat {ABy’}\) = \(\widehat {BAx}\) = 50o.====== **** mời các bạn xem câu tiếp bên dưới **** =====