Câu hỏi:
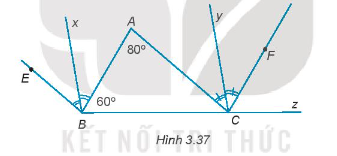
Gọi Bx, Cy lần lượt là tia phân giác của các góc BE và ACF. Chứng minh rằng Bxx // Cy.
Trả lời:
Hướng dẫn giải:
Vì Bx là tia phân giác của góc \(\widehat {ABE}\) nên \(\widehat {EBx} = \widehat {xBA} = \frac{{\widehat {EBA}}}{2} = \frac{{80^\circ }}{2} = 40^\circ \)
Vì Cy là tia phân giác của góc \(\widehat {ACF}\) nên \(\widehat {ACy} = \widehat {yCF} = \frac{{\widehat {ACF}}}{2} = \frac{{80^\circ }}{2} = 40^\circ \)
Ta có BC cắt Bx và cắt Cy tạo ra cặp góc đồng vị là \[\widehat {zCy}\] và \(\widehat {zBx}\).
Ta có:
\[\widehat {zCy}\] = \(\widehat {yCF}\)+ \(\widehat {FCz}\) = 40o + 60o = 100o.
\(\widehat {zBx}\)= \(\widehat {xBA}\)+ \(\widehat {ABC}\) = 40o + 60o = 100o.
Suy ra, \[\widehat {zCy}\] = \(\widehat {zBx}\)= 100o
Vì \[\widehat {zCy}\] và \(\widehat {zBx}\) là hai góc đồng vị và \[\widehat {zCy}\] = \(\widehat {zBx}\) nên Bx // Cy.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- A. Câu hỏi (trắc nghiệm)
Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia ON là tia đối của tia OM. Khi đó cặp góc đối đỉnh là cặp góc nào trong các cặp góc sau đây?
Câu hỏi:
A. Câu hỏi (trắc nghiệm)
Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia ON là tia đối của tia OM. Khi đó cặp góc đối đỉnh là cặp góc nào trong các cặp góc sau đây?A. \(\widehat {BOM}\) và \(\widehat {CON}\);
B. \(\widehat {AOB}\) và \(\widehat {AON}\);
C. \(\widehat {AOM}\) và \(\widehat {CON}\);
Đáp án chính xác
D. \(\widehat {COM}\) và \(\widehat {CON}\).
Trả lời:
Lời giải:
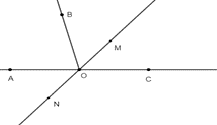
Từ hình vẽ ta thấy cặp góc đối đỉnh là \(\widehat {AOM}\) và \(\widehat {CON}\) vì OA là tia đối của tia OC và OM là tia đối của tia ON.
Đáp án đúng là C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong các khẳng định sau, khẳng định nào đúng?
Câu hỏi:
Trong các khẳng định sau, khẳng định nào đúng?
A. Hai góc bằng nhau thì đối đỉnh;
B. Hai góc không đối đỉnh thì không bằng nhau;
C. Hai góc đối đỉnh thì bằng nhau;
Đáp án chính xác
D. Cả ba khẳng định trên đều đúng.
Trả lời:
Lời giải:
Khẳng định đúng là: Hai góc đối đỉnh thì bằng nhau.
Đáp án đúng là C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Biết số đo của một trong bốn góc đó là 65o. Khi đó số đo của ba góc còn lại là:
Câu hỏi:
Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Biết số đo của một trong bốn góc đó là 65o. Khi đó số đo của ba góc còn lại là:
A. 65o; 115o; 120o;
B. 65o; 65o; 115o;
C. 115o; 115o; 50o;
D. 65o; 115o; 115o.
Đáp án chính xác
Trả lời:
Lời giải:
Giả sử: đừng thẳng a cắt đường thẳng b tại O, tạo thành 4 góc \(\widehat {{O_1}};\widehat {{O_2}};\widehat {{O_3}};\widehat {{O_4}}\) và \(\widehat {{O_1}}\) = 65o.
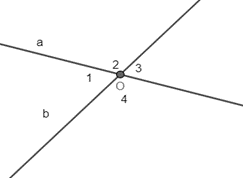
Vì \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) đối đỉnh nên \(\widehat {{O_1}}\) = \(\widehat {{O_3}}\) = 65o.
Vì \(\widehat {{O_3}}\) và \(\widehat {{O_4}}\) kề bù nên \(\widehat {{O_3}}\) + \(\widehat {{O_4}}\) = 180o.
Thay số: 65o + \(\widehat {{O_4}}\) = 180o
\(\widehat {{O_4}}\) = 180o – 65o = 115o.
Mà \(\widehat {{O_4}}\) và \(\widehat {{O_2}}\) đối đỉnh nên \(\widehat {{O_4}}\) = \(\widehat {{O_2}}\) = 115o.
Vậy \(\widehat {{O_4}}\) = \(\widehat {{O_2}}\) = 115o; \(\widehat {{O_1}}\) = \(\widehat {{O_3}}\) = 65o.
Đáp án đúng là D.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Số đo của bốn góc đó có thể là trường hợp nào trong các trường hợp sau đây?
Câu hỏi:
Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Số đo của bốn góc đó có thể là trường hợp nào trong các trường hợp sau đây?
A. 70o; 70o; 70o; 110o;
B. 60o; 120o; 120o;120o;
C. 80o; 50o; 130o; 100o;
D. 90o; 90o; 90o; 90o.
Đáp án chính xác
Trả lời:
Lời giải:
Vì hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt nên sẽ có hai cặp góc đối đỉnh.
Mà các góc đối đỉnh thì bằng nhau. Do đó, trong bốn giá trị sẽ lần lượt có hai cặp giá trị góc bằng nhau.
Nhận thấy chỉ có đáp án D thỏa mãn.
Vậy đáp án đúng là D.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hai đường thẳng AB và CD cắt nhau tại O. Cho OM là tia phân giác của góc BOD và \(\widehat {BOM} = 30^\circ \). Số đo của góc AOC bằng:
Câu hỏi:
Hai đường thẳng AB và CD cắt nhau tại O. Cho OM là tia phân giác của góc BOD và \(\widehat {BOM} = 30^\circ \). Số đo của góc AOC bằng:
A. 30o;
B. 60o;
Đáp án chính xác
C. 120o;
D. Một kết quả khác.
Trả lời:
Lời giải:
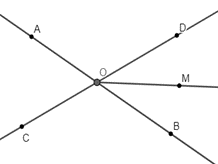
Vì OM là tia phân giác của góc BOD nên \(\widehat {BOM} = \widehat {MOD} = \frac{{\widehat {BOD}}}{2} = 30^\circ \)
Suy ra \(\widehat {BOD}\) = 2.30o = 60o.
Lại có, \(\widehat {BOD}\) và \(\widehat {AOC}\) là hai góc đối đỉnh nên \(\widehat {BOD}\) = \(\widehat {AOC}\) = 60o.
Đáp án đúng là B.====== **** mời các bạn xem câu tiếp bên dưới **** =====