Câu hỏi:
Nối cột A với cột B để được một phát biểu đúng.Cột A Cột BHình vuông không có trục đối xứng, cũng không có tâm đối xứng.Hình trònkhông có trục đối xứng nhưng có tâm đối xứng.Hình thoicó vố số trục đối xứng.Hình thangcó bốn trục đối xứng.Hình bình hànhcó hai trục đối xứng.
Trả lời:
Hình vuông là hình có 4 trục đối xứng là hai đường chéo và hai đường nối trung điểm của các cặp cạnh đối diện.Hình tròn là hình có vô số trục đối xứng là các đường thẳng đi qua tâm.Hình thoi là hình có hai trục đối xứng là hai đường chéo.Hình thang không có trục đối xứng và cũng có tâm đối xứng.Hình bình hành là hình không có trục đối xứng và có tâm đối xứng.Ta hoàn thành bảng ghép cột như sau: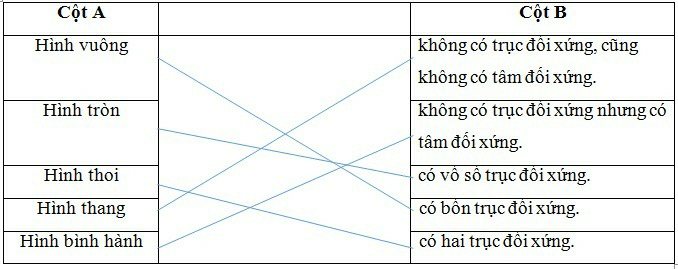
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Lý thuyết Toán lớp 6 Chương 5 (Kết nối tri thức 2023): Tính đối xứng của hình phẳng trong tự nhiên hay, chi tiết
Lý thuyết Toán lớp 6 Chương 5: Tính đối xứng của hình phẳng trong tự nhiên
Video giải Toán 6 Chương 5: Tính đối xứng của hình phẳng trong tự nhiên – Kết nối tri thức
A. Lý thuyết Toán lớp 6 Chương 5: Tính đối xứng của hình phẳng trong tự nhiên
1. Hình có trục đối xứng trong thực tế
Các hình có một đường thẳng d chia hình đó thành hai phần mà nếu “gấp” hình theo đường thẳng d thì hai phần đó “chồng khít” lên nhau. Những hình như thế được gọi là hình có trục đối xứng và đường thẳng d là trục đối xứng của nó.
2. Trục đối xứng của một số hình phẳng
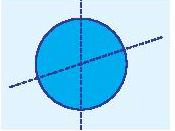
Mỗi đường thẳng đi qua tâm là một trục đối xứng của hình tròn. Do đó hình tròn có vô số trục đối xứng.
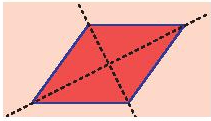
Mỗi đường chéo là một trục đối xứng của hình thoi.
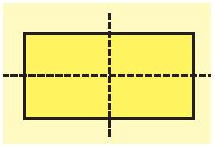
Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.
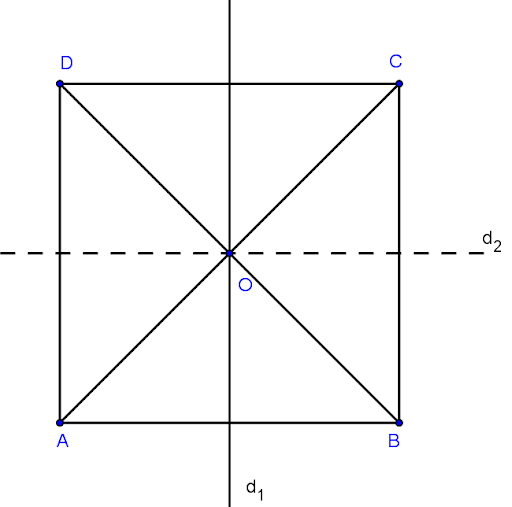
Hình vuông có 4 trục đối xứng bao gồm: Hai đường thẳng đi qua trung điểm hai cạnh đối điện và hai đường chéo.
3. Hình có tâm đối xứng trong thực tế
Mỗi hình có mổ điểm O, mà khi quay hình đó xung quanh điểm O đúng một nửa vòng thì hình thu được “trùng khít” với chính nó ở vị trí ban đầu (trước khi quay).
Những hình như thế được gọi là “hình có tâm đối xứng” và điểm O được gọi là “tâm đối xứng” của hình.
4. Tâm đối xứng của một số hình phẳng
Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.
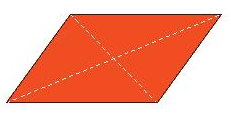
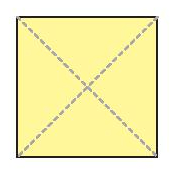
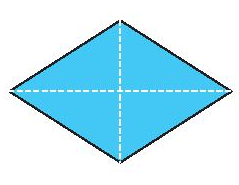
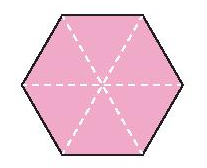
Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
B. Bài tập
Bài 1. Trong các hình bên, em hãy chỉ ra:
a) Những hình có tâm đối xứng;
b) Những hình có trục đối xứng.
Lời giải
a) Những hình có tâm đối xứng là: cánh quạt.
b) Những hình có trục đối xứng là: tam giác đều, trái tim và cánh diều.
Bài 2. Nối cột A với cột B để được một phát biểu đúng.
Cột A
Cột B
Hình vuông
không có trục đối xứng, cũng không có tâm đối xứng.
Hình tròn
không có trục đối xứng nhưng có tâm đối xứng.
Hình thoi
có vố số trục đối xứng.
Hình thang
có bốn trục đối xứng.
Hình bình hành
có hai trục đối xứng.
Lời giải
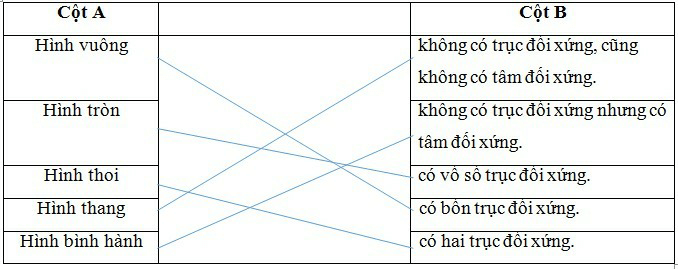
Hình vuông là hình có 4 trục đối xứng là hai đường chéo và hai đường nối trung điểm của các cặp cạnh đối diện.
Hình tròn là hình có vô số trục đối xứng là các đường thẳng đi qua tâm.
Hình thoi là hình có hai trục đối xứng là hai đường chéo.
Hình thang không có trục đối xứng và cũng có tâm đối xứng.
Hình bình hành là hình không có trục đối xứng và có tâm đối xứng.
Ta hoàn thành bảng ghép cột như sau:
Xem thêm các bài tóm tắt lý thuyết Toán 6 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Chương 4: Một số hình phẳng trong thực tiễn
Lý thuyết Chương 5: Tính đối xứng của hình phẳng trong tự nhiên
Lý thuyết Chương 6: Phân số
Lý thuyết Chương 7: Số thập phân
Lý thuyết Chương 8: Những hình học cơ bản
- Sách bài tập Toán 6 (Kết nối tri thức) Ôn tập chương 5 trang 91, 92, 93
Giải SBT Toán lớp 6 Ôn tập chương 5 trang 91, 92, 93
Câu hỏi (Trắc Nghiệm)
Bài 1 trang 90 sách bài tập Toán lớp 6 Tập 1: Trong các câu sau, câu nào đúng?
(A) Tam giác đều có 6 trục đối xứng;
(B) Hình chữ nhật với hai kích thước khác nhau có 4 trục đối xứng;
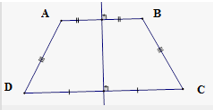
(C) Hình thang cân, góc ở đáy khác 90o, có đúng một trục đối xứng;
(D) Hình bình hành có hai trục đối xứng.
Lời giải:
(A). Sai vì tam giác đều có 3 trục đối xứng
(B). Sai vì hình chữ nhật có 2 trục đối xứng
(D). Sai vì hình bình hành không có trục đối xứng
(C). Đúng vì hình thang cân, góc ở đáy khác 90o, có đúng một trục đối xứng là đường thẳng đi qua trung điểm hai đáy của hình thang cân.
Đáp án cần chọn là: C
Bài 2 trang 90 sách bài tập Toán lớp 6 Tập 1: Trong các câu sau, câu nào sai?
(A) Hình vuông có đúng 4 trục đối xứng;
(B) Hình thoi, các góc khác 90o, có đúng 2 trục đối xứng;
(C) Hình lục giác đều có đúng 3 trục đối xứng;
(D) Hình chữ nhật với hai kích thước khác nhau có đúng hai trục đối xứng.
Lời giải:
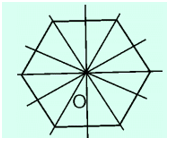
(C). Sai vì hình lục giác đều có 6 trục đối xứng gồm 3 đường thẳng đi qua hai đỉnh đối diện và 3 đường thẳng đi qua trung điểm của hai cạnh đối diện như hình vẽ dưới
Đáp án cần chọn là: C
Bài 3 trang 91 sách bài tập Toán lớp 6 Tập 1: Trong các câu sau, câu nào đúng?
(A) Hình tam giác đều có tâm đối xứng là giao điểm của ba trục đối xứng;
(B) Hình chữ nhật có tâm đối xứng là giao của hai đường chéo;
(C) Hình thang cân, góc ở đáy khác 90o, có tâm đối xứng là giao điểm của hai đường chéo;
(D) Hình thang có tâm đối xứng là giao điểm của hai đường chéo.
Lời giải:
(A). Sai vì tam giác đều không có tâm đối xứng.
(B). Đúng
(C). Sai vì hình thang cân không có tâm đối xứng.
(D). Sai vì hình thang không có tâm đối xứng.
Đáp án cần chọn là: B
Bài 4 trang 91 sách bài tập Toán lớp 6 Tập 1: Trong các câu sau, câu nào sai?
(A) Hình lục giác đều có 6 tâm đối xứng;
(B) Hình thoi có tâm đối xứng là giao điểm của hai đường chéo;
(C) Hình tròn có tâm đối xứng là tâm của đường tròn;
(D) Hình vuông có tâm đối xứng là giao điểm của hai đường chéo.
Lời giải:
(A) Sai vì hình lục giác đều có 1 tâm đối xứng.
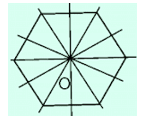
Đáp án cần chọn là: A
Bài tập
Bài 5.22 trang 91 sách bài tập Toán lớp 6 Tập 1: Đoạn thẳng AB có độ dài 4 cm. Gọi O là tâm đối xứng của đoạn thẳng AB. Tính độ dài đoạn OA.
Lời giải:
Vì O là tâm đối xứng của đoạn thẳng AB nên O là trung điểm của đoạn thẳng AB
Do đó độ dài đoạn thẳng AB gấp đôi độ dài đoạn thẳng OA hay độ dài đoạn thẳng OA bằng nửa độ dài đoạn thẳng AB.
Độ dài đoạn OA dài là: 4: 2 = 2 (cm)
Vậy OA = 2cm.
Bài 5.23 trang 91 sách bài tập Toán lớp 6 Tập 1: Quan sát các hình dưới đây:
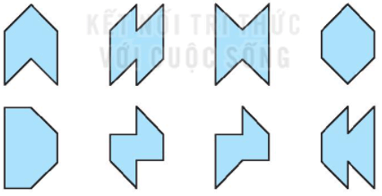
a) Có bao nhiêu hình có tâm đối xứng?
b) Có bao nhiêu hình có đúng một trục đối xứng?
c) Có bao nhiêu hình có cả tâm đối xứng và trục đối xứng?
d) Có bao nhiêu hình không có cả tâm đối xứng lẫn trục đối xứng?
Lời giải:
a) Có 4 hình có tâm đối xứng là:
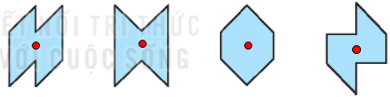
b) Có 3 hình có đúng 1 trục đối xứng;
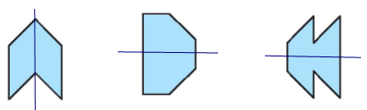
c) Có 2 hình có cả tâm đối xứng và trục đối xứng;
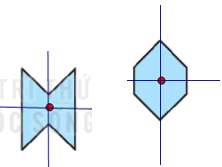
d) Có 1 hình không có tâm đối xứng và trục đối xứng;
Bài 5.24 trang 92 sách bài tập Toán lớp 6 Tập 1: Em hãy hoàn thiện các bức vẽ dưới đây để thu được các hình có trục đối xứng d.
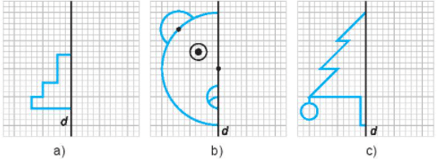
Lời giải:
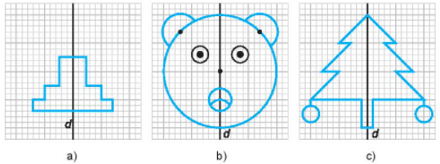
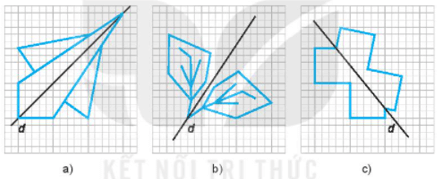
Bài 5.25 trang 92 sách bài tập Toán lớp 6 Tập 1: Em hãy hoàn thiện các bước vẽ dưới đây để thu được các hình có trục đối xứng d.
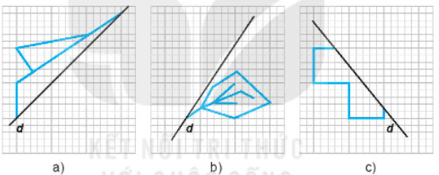
Lời giải:
Bài 5.26 trang 92 sách bài tập Toán lớp 6 Tập 1: Em hãy hoàn thiện các bức vẽ dưới đây để thu được các hình có tâm đối xứng O.
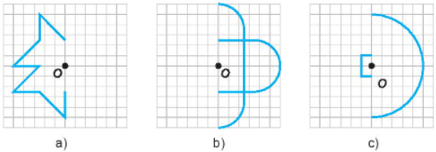
Lời giải:
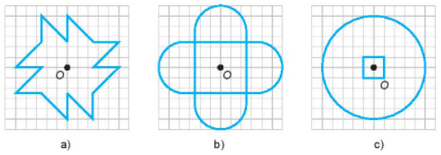
Bài 5.27 trang 93 sách bài tập Toán lớp 6 Tập 1: Em hãy hoàn thiện các bức vẽ dưới đây để thu được các hình có trục đối xứng d và tâm đối xứng O.
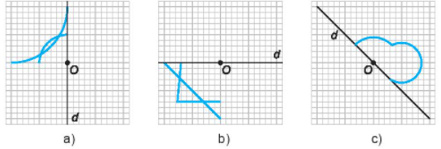
Lời giải:
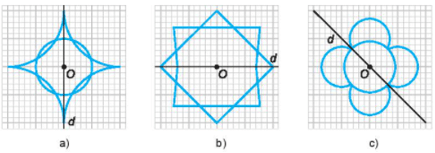
Bài 5.28 trang 93 sách bài tập Toán lớp 6 Tập 1: Em hãy ghép hai tấm thẻ trong các thẻ số dưới đây để được một hình chỉ một số có hai chữ số sao cho:
a) Hình đó có trục đối xứng.
b) Hình đó có tâm đối xứng.
Trong mỗi trường hợp, em có thể ghép được tất cả bao nhiêu “số” như vậy?
Lời giải:
a) Ta có 6 số có trục đối xứng: 10, 80, 18, 81, 25, 52.
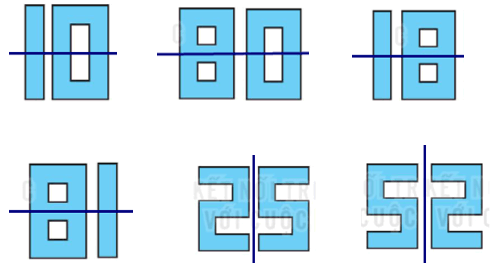
b) Ta có hai số có tâm đối xứng: 69, 96.
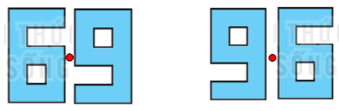
Bài 5.29 trang 93 sách bài tập Toán lớp 6 Tập 1: Hình thoi ABCD có tâm đối xứng O. Biết OA = 3cm, OB = 2 cm. Hãy tính diện tích hình thoi.
Lời giải:
Vì O là tâm đối xứng của hình thoi ABCD nên O là giao điểm của hai đường chéo AC và BD.
Do đó độ dài đoạn thẳng AC gấp hai lần độ dài đoạn thẳng OA nên AC = 2. 3 = 6 (cm)
Độ dài đoạn thẳng BD gấp hai lần độ dài đoạn thẳng OB nên BD = 2. 2 = 4 (cm)
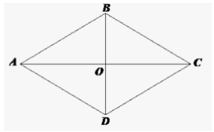
Diện tích hình thoi ABCD là:
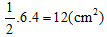
Vậy diện tích hình thoi là 12 cm2.
- Em hãy vẽ các hình dưới đây vào giấy kẻ ô vuông rồi chỉ ra tất cả các trục đối xứng của chúng (nếu có)
Câu hỏi:
Em hãy vẽ các hình dưới đây vào giấy kẻ ô vuông rồi chỉ ra tất cả các trục đối xứng của chúng (nếu có)
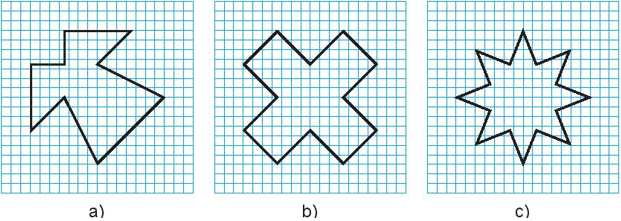
Trả lời:
+) Hình a) có 1 trục đối xứng.
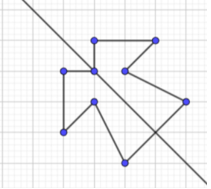+) Hình b) có 4 trục đối xứng
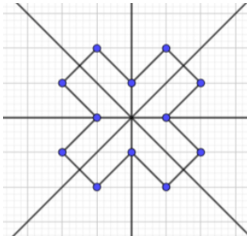+) Hình c) có 8 trục đối xứng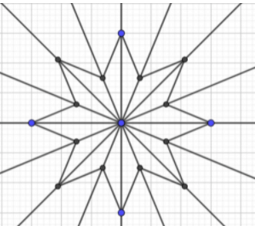
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hình nào dưới đây là hình có tâm đối xứng?
Câu hỏi:
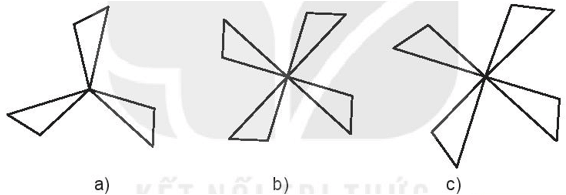
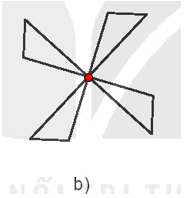
Hình nào dưới đây là hình có tâm đối xứng?
Trả lời:
Hình b) có tâm đối xứng
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Vẽ các hình sau vào vở và vẽ thêm họa tiết để được hình mặt cười nhận đường thẳng d cho trước là trục đối xứng
Câu hỏi:
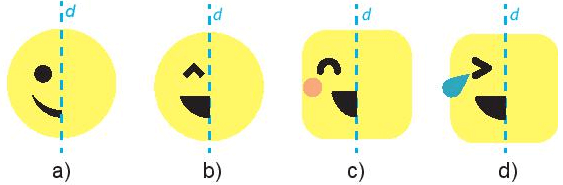
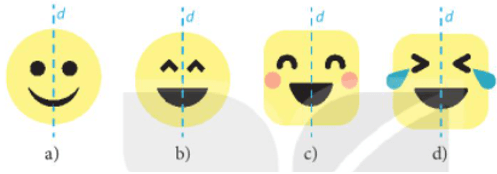
Vẽ các hình sau vào vở và vẽ thêm họa tiết để được hình mặt cười nhận đường thẳng d cho trước là trục đối xứng
Trả lời:
Vẽ thêm họa tiết để được hình mặt cười nhận đường thẳng d cho trước là trục đối xứng là:
====== **** mời các bạn xem câu tiếp bên dưới **** =====