Câu hỏi:
Một lớp có 22 nữ sinh và 18 nam sinh. Hãy tính tỉ số phần trăm của nữ sinh so với tổng số học sinh cả lớp, tỉ số phần trăm của nam sinh so với tổng số học sinh của cả lớp.
Trả lời:
Tổng số học sinh của lớp là:
22 + 18 = 40 (học sinh)
Tỉ số học sinh nữ so với học sinh của lớp là: 22:40 = 0,55 = 55%Tỉ số học sinh nam so với học sinh của lớp là: 18: 40 = 0,45 = 45%Đáp số: 55% và 45%
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Lý thuyết Tỉ số và tỉ số phần trăm (Chân trời sáng tạo 2023) hay, chi tiết | Toán lớp 6
Lý thuyết Toán lớp 6 Bài 4: Tỉ số và tỉ số phần trăm
Video giải Toán 6 Bài 4: Tỉ số và tỉ số phần trăm – Chân trời sáng tạo
A. Lý thuyết Tỉ số và tỉ số phần trăm
1. Tỉ số của hai đại lượng
Ta gọi thương trong phép chia số a cho số b (b ≠0) là tỉ số của a và b.
Tỉ số của a và b kí hiệu là a : b (cũng kí hiệu là
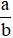).Ví dụ 1.
– Tỉ số của hai số 16 và 37 được kí hiệu là 16 : 37 hay
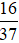.– Tỉ số của hai số 3,6 và 8,25 được kí hiệu là 3,6 : 8,25 hay
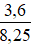.Chú ý:
– Phân số
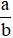thì cả a và b phải là các số nguyên.– Tỉ số
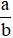thì a và b có thể là các số nguyên, phân số, hỗn số, số thập phân,…– Ta thường dùng khái niệm tỉ số nói về thương của hai đại lượng cùng loại và cùng đơn vị đo.
Ví dụ 2. Tính tỉ số của hai đại lượng được cho trong các trường hợp sau:
a) 0,6 kg và 260 g;
b) 15 phút và
giờ.Lời giải:
a) Đổi 0,6 kg = 600 g
Tỉ số của hai đại lượng 0,4 kg và 340 g hay tỉ số của 400 g và 340 g là:
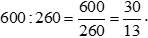.Vậy tỉ số của hai đại lượng 0,6 kg và 260 g là
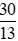.b)
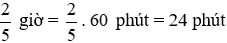
Tỉ số của hai đại lượng 15 phút và
giờ hay tỉ số của 15 phút và 24 phút là: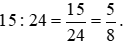
Vậy tỉ số của hai đại lượng 15 phút và
giờ là 
.2. Tỉ số phần trăm của hai đại lượng
Trong thực hành, ta thường dùng tỉ số dưới dạng tỉ số phần trăm với kí hiệu % thay cho
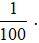.Để tính tỉ số phần trăm của hai số a và b, ta nhân a với 100 rồi chia cho b và viết kí hiệu % vào bên phải kết quả tìm được.
Ví dụ 3. Tính tỉ số phần trăm của hai số cho trong mỗi trường hợp sau:
a) 2 và 8;
b)
và 3,125.Lời giải:
a) Tỉ số phần trăm của hai số 2 và 8 là:
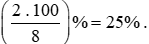
Vậy tỉ số phần trăm của hai số 2 và 8 là 25%.
b) Tỉ số phần trăm của hai số
và 3,125 là: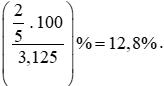
Vậy tỉ số phần trăm của hai số
và 3,125 là 12,8%.B. Bài tập tự luyện
Bài 1. Lớp 6A có 36 học sinh, trong đó có 20 học sinh nữ. Tính tỉ số giữa học sinh nam so với số học sinh cả lớp.
Lời giải:
Số học sinh nam của lớp 6A là:
36 −20 = 16 (học sinh).
Tỉ số giữa học sinh nam so với số học sinh cả lớp là:
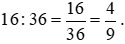
Vậy tỉ số giữa học sinh nam so với số học sinh cả lớp là
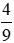.Bài 2. Viết các số thập phân sau đây dưới dạng tỉ số phần trăm:
−0,56; 7,5; −3,25.
Lời giải:
Các số thập phân được viết dưới dạng tỉ số phần trăm như sau:
−0,56 = −0,56 . 100% = −56%;
7,5 = 7,5 . 100% = 75%;
−3,25 = −12,25 . 100% = −325%.
Bài 3. Viết các phân số sau dưới dạng tỉ số phần trăm:
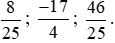
Lời giải:
Để viết các phân số dưới dạng tỉ số phần trăm, ta làm như sau:
Bước 1: Viết các phân số dưới dạng phân số có mẫu là 100.
Bước 2: Thêm kí hiệu % vào sau tử số của phân số mới.
Các phân số được viết dưới dạng tỉ số phần trăm là:
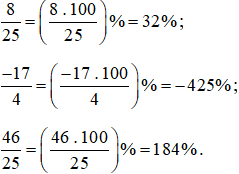
Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 3: Làm tròn số thập phân và ước lượng kết quả
Lý thuyết Bài 4: Tỉ số và tỉ số phần trăm
Lý thuyết Bài 5: Bài toán về tỉ số phần trăm
Lý thuyết Bài 1: Hình có trục đối xứng
Lý thuyết Bài 2: Hình có tâm đối xứng
- Một lớp có 22 nữ sinh và 18 nam sinh. Hãy tính tỉ số phần trăm của nữ sinh so với tổng số học sinh cả lớp, tỉ số phần trăm của nam sinh so với tổng số học sinh của cả lớp.
Câu hỏi:
Một lớp có 22 nữ sinh và 18 nam sinh. Hãy tính tỉ số phần trăm của nữ sinh so với tổng số học sinh cả lớp, tỉ số phần trăm của nam sinh so với tổng số học sinh của cả lớp.
Trả lời:
Tổng số học sinh của lớp là:
22 + 18 = 40 (học sinh)Tỉ số học sinh nữ so với học sinh của lớp là:
Tỉ số học sinh nam so với học sinh của lớp là:
18: 40 = 0,45 = 45%Đáp số: 55% và 45%====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Một số sau khi giảm đi 20% thì phải tăng thêm bao nhiêu phần trăm số mới để lại được số cũ.
Câu hỏi:
Một số sau khi giảm đi 20% thì phải tăng thêm bao nhiêu phần trăm số mới để lại được số cũ.
Trả lời:
Một số giảm đi 20% tức là giảm đi 1/5 giá trị của số đó.
Vậy phải tăng số mới thêm 1/4 của nó tức là 25% thì được số ban đầu====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Lượng nước trong cỏ tươi là 55%, trong cỏ khô là 10%. Hỏi phơi 100 kg cỏ tươi ta được bao nhiêu ki lô gam cỏ khô.
Câu hỏi:
Lượng nước trong cỏ tươi là 55%, trong cỏ khô là 10%. Hỏi phơi 100 kg cỏ tươi ta được bao nhiêu ki lô gam cỏ khô.
Trả lời:
Lượng cỏ có trong cỏ tươi là:
100 – 55 = 45%
Hay 100 kg cỏ tươi có 45 kg cỏ.
Nhưng trong cỏ khô còn có 10% nước. Nên 45 kg cỏ là 90% khối lượng trong cỏ khô.Vậy 100 kg cỏ tươi thu được số cỏ khô là:
Đáp số: 50kg====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Nước biển chứa 4% muối. Cần đổ thêm bao nhiêu gam nước lã vào 400 gam nước biển để tỉ lệ muối trong dung dịch là 2%.
Câu hỏi:
Nước biển chứa 4% muối. Cần đổ thêm bao nhiêu gam nước lã vào 400 gam nước biển để tỉ lệ muối trong dung dịch là 2%.
Trả lời:
Lượng nước muối có trong 400g nước biển là:
400 x 4: 100 = 16 (g)
Dung dịch chứa 2 % muối là:
Cứ có 100 g nước thì có 2 g muối
16 g muối cần số lượng nước là:
100: 2 x 16 = 800 (g)
Lượng nước phải thêm là:
800 – 400 = 400 (g)Đáp số 400 g.====== **** mời các bạn xem câu tiếp bên dưới **** =====