Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Vectơ trong không gian, quan hệ vuông góc – bản 1
CHƯƠNG 3. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC
Bài 1. Vectơ trong không gian. sự đồng phẳng của các vectơ
A. Tóm tắt lí thuyết
I. Vectơ trong không gian.
a. Quy tắc ba điểm: Với ba điểm bất kì A, B, C ta có \[\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \].
b. Quy tắc hình bình hành: Nếu OABC là hình bình hành thì \[\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} \]
c. Quy tắc phân tích một vectơ thành hiệu của hai vectơ cùng gốc:
\[\overrightarrow {AB} = \overrightarrow {OB} – \overrightarrow {OA} \], với mọi điểm O.
d. I là trung điểm đoạn thẳng AB khi và chỉ khi
\[\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \Leftrightarrow \overrightarrow {OI} = \frac{{\overrightarrow {OA} + \overrightarrow {OB} }}{2}\], với mọi điểm O. (i)
e. G là trọng tâm tam giác ABC khi và chỉ khi
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {OG} = \frac{{\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} }}{3}\], với mọi điểm O. (ii)
Lưu ý. Khi gặp tổng hai vectơ cùng gốc hoặc tổng ba vectơ cùng gốc ta thường sử dụng (i), (ii).
f. Quy tắc hình hộp (để cộng ba vectơ khác \[\overrightarrow 0 \] không đồng phẳng):
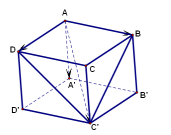
Cho hình hộp \[ABCD.A’B’C’D’\].
Khi đó: \[\overrightarrow {AC’} = \overrightarrow {AA’} + \overrightarrow {AB} + \overrightarrow {AD} \].
g. \[\overrightarrow a \] cùng phương \[\overrightarrow b \] (\[\overrightarrow b \ne \overrightarrow 0 \]) ⇔ ∃k ∈ R : \[\overrightarrow a = k\overrightarrow b \].
2. Sự đồng phẳng của các vectơ. Điều kiện để ba vectơ đồng phẳng.
Định nghĩa 1. Ba vectơ gọi là đồng phẳng nếu giá của chúng cùng song song với một mặt phẳng.
Định lí 1 (Điều kiện để ba vectơ đồng phẳng).
Cho ba vectơ \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \] trong đó \[\overrightarrow a \] và \[\overrightarrow b \] không cùng phương. Điều kiện cần và đủ để \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \] đồng phẳng là có các số m, n sao cho \[\overrightarrow c = m\overrightarrow a + n\overrightarrow b \]. Hơn nữa, các số m, n là duy nhất.
Chú ý 1. Ba vectơ \[\overrightarrow {OA} ,\overrightarrow {OB} ,\overrightarrow {OC} \] đồng phẳng khi và chỉ khi bốn điểm O, A, B, C đồng phẳng, tức là ba đường thẳng OA, OB, OC cùng nằm trong một mặt phẳng.
Định lí 2 (Biểu thị một vectơ theo ba vectơ không đồng phẳng).
Nếu \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \] là ba vectơ không đồng phẳng thì với mỗi vectơ \[\overrightarrow d \], luôn tồn tại các số m, n, p sao cho \[\overrightarrow d = m\overrightarrow a + n\overrightarrow b + p\overrightarrow c \]. Hơn nữa các số m, n, p là duy nhất.
B. Một số dạng toán
Dạng 1. Chứng minh các đẳng thức vectơ. Biểu thị một vectơ theo các vectơ không đồng phẳng.
Phương pháp. Dựa vào các quy tắc, tính chất và các hệ thức vectơ thường dùng.
Bài 1. Cho hình hộp \[ABCD.A’B’C’D’\].
Hãy biểu diễn các vectơ \[\overrightarrow {AC’} ,\overrightarrow {BD’} ,\overrightarrow {CA’} ,\overrightarrow {DB’} ,\overrightarrow {BC’} ,\overrightarrow {A’D} \]
theo các vectơ\[\;\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} \; = \overrightarrow b ,\overrightarrow {AA’} = \overrightarrow c \].
Lời giải
Ta có
\[\overrightarrow {AC’} = \overrightarrow {AB} + \overrightarrow {BB’} + \overrightarrow {B’C’} = \overrightarrow a + \overrightarrow c + \overrightarrow b \]
\[\overrightarrow {BD’} = \overrightarrow {BA} + \overrightarrow {AD} + \overrightarrow {DD’} = – \overrightarrow a + \overrightarrow b + \overrightarrow c \]
\[\overrightarrow {CA’} = \overrightarrow {CD} + \overrightarrow {DA} + \overrightarrow {AA’} = – \overrightarrow a – \overrightarrow b + \overrightarrow c \]
\[\overrightarrow {DB’} = \overrightarrow {DC} + \overrightarrow {CB} + \overrightarrow {BB} = \overrightarrow a – \overrightarrow b + \overrightarrow c \]
\[\overrightarrow {BC’} = \overrightarrow {BC} + \overrightarrow {CC’} = \overrightarrow b + \overrightarrow c \]
\[\overrightarrow {A’D} = \overrightarrow {A’D’} + \overrightarrow {D’D} = \overrightarrow b – \overrightarrow c \]
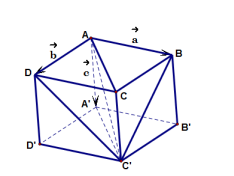
Bài 2. Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD và O là trung điểm đoạn thẳng AG. Chứng minh rằng:
a) \[3\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \].
b) \[3\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 6\overrightarrow {MO} \] (M là điểm bất kì trong không gian).
Lời giải
a) Vì G là trọng tâm của tam giác BCD nên \[3\overrightarrow {OG} = \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \]. Vì O là trung điểm đoạn thẳng AG nên \[\overrightarrow {OA} + \overrightarrow {OG} = \overrightarrow 0 \]. Do đó
\[3\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = 3(\overrightarrow {OA} + \overrightarrow {OG} ) = \overrightarrow 0 \].
b) Theo quy tắc ba điểm ta có
\[3\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} \]
\[ = 3\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + \overrightarrow {MO} + \overrightarrow {OB} + \overrightarrow {MO} + \overrightarrow {OC} + \overrightarrow {MO} + \overrightarrow {OD} \]
\[ = 6\overrightarrow {MO} + 3\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = 6\overrightarrow {MO} \]
Lưu ý. Có thể giải câu b) như sau: Do G là trọng tâm ∆BCD nên
\[\overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 3\overrightarrow {MG} \].
Do đó
\[\begin{array}{l}3\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 3\overrightarrow {MA} + 3\overrightarrow {MG} \\ = 3\left( {\overrightarrow {MA} + \overrightarrow {MG} } \right) = 6\overrightarrow {MO} \end{array}\].
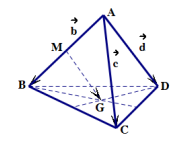
Bài 3. Cho tứ diện ABCD. Gọi M là trung điểm AB và G là trọng tâm tam giác BCD. Đặt \[\;\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} \; = \overrightarrow c ,\overrightarrow {AD} = \overrightarrow d \]. Phân tích \[\overrightarrow {MG} \] theo \[\overrightarrow b ,\overrightarrow c ,\overrightarrow d \].
Lời giải
Ta có
\[\overrightarrow {MG} = \frac{1}{3}\left( {\overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} } \right)\]
\[ = \frac{1}{3}\left[ {\frac{1}{2}\overrightarrow {AB} + (\overrightarrow {MA} + \overrightarrow {AC} ) + (\overrightarrow {MA} + \overrightarrow {AD} )} \right]\]
\[ = \frac{1}{3}\left[ {\frac{1}{2}\overrightarrow b – \frac{1}{2}\overrightarrow b + \overrightarrow c – \frac{1}{2}\overrightarrow b + \overrightarrow d } \right]\]
\[ = – \frac{1}{6}\overrightarrow b + \frac{1}{3}\overrightarrow c + \frac{1}{3}\overrightarrow d \].
Bài 4. Cho hình chóp S.ABCD.
a) Chứng minh rằng nếu ABCD là hình bình hành thì
\[\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \].
Điều ngược lại đúng không?
b) Gọi O là giao điểm của AC và BD. Chứng tỏ rằng ABCD là hình bình hành khi và chỉ khi \[\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow {SO} \].
Lời giải
a) Ta có sự tương đương:
\[\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \Leftrightarrow \overrightarrow {SB} – \overrightarrow {SA} = \overrightarrow {SC} – \overrightarrow {SD} \]
\[ \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \] ⇔ ABCD là hình bình hành (do ABCD đã là tứ giác rồi).
Vậy nếu ABCD là hình bình hành thì \[\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \]. Chiều ngược lại cũng đúng.
b) Giả sử ABCD là hình bình hành. Khi đó:
\[\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} \]
\[ = \overrightarrow {SO} + \overrightarrow {OA} + \overrightarrow {SO} + \overrightarrow {OB} + \overrightarrow {SO} + \overrightarrow {OC} + \overrightarrow {SO} + \overrightarrow {OD} \]
\[ = 4\overrightarrow {SO} + (\overrightarrow {OA} + \overrightarrow {OC} ) + (\overrightarrow {OB} + \overrightarrow {OD} ) = 4\overrightarrow {SO} \].
Giả sử \[\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \]. Gọi I, J theo thứ tự là trung điểm của AC, BD. Khi đó:
\[\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} \]
\[\begin{array}{l} = 4\overrightarrow {SO} + (\overrightarrow {OA} + \overrightarrow {OC} ) + (\overrightarrow {OB} + \overrightarrow {OD} )\\ = 4\overrightarrow {SO} + 2(\overrightarrow {OI} + 2\overrightarrow {OJ} )\end{array}\]
Bởi vậy: \[\overrightarrow {OI} + \overrightarrow {OJ} = \overrightarrow 0 \]. Suy ra O là trung điểm I J. Suy ra I ∈ BD và J ∈ AC. Do đó I ≡ J ≡ O. Vậy hai đường chéo AC và BD có cùng chung trung điểm. Suy ra ABCD là hình bình hành.
Cách khác. Ta có \[\overrightarrow {OC} = k\overrightarrow {OA} ,\overrightarrow {OD} = m\overrightarrow {OB} \]. Do đó:
\[\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \]
\[ \Leftrightarrow (\overrightarrow {SO} + \overrightarrow {OA} ) + (\overrightarrow {SO} + \overrightarrow {OB} ) + (\overrightarrow {SO} + \overrightarrow {OC} ) + (\overrightarrow {SO} + \overrightarrow {OD} ) = 4\overrightarrow {SO} \]
\[ \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \]
# » SA + # »SB + # » SC +
# » SD = 4 # » SO
⇔( # » SO
\[\begin{array}{l} \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} + k\overrightarrow {OA} + m\overrightarrow {OB} = \overrightarrow 0 \\ \Leftrightarrow (1 + k)\overrightarrow {OA} + (1 + m)\overrightarrow {OB} = \overrightarrow 0 \end{array}\]
\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{1 + k = 0}\\{1 + m = 0}\end{array}} \right.\] (do \[\overrightarrow {OA} \] và \[\overrightarrow {OB} \] không cùng phương)
\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{k = – 1}\\{m = – 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\overrightarrow {OC} = – \overrightarrow {OA} }\\{\overrightarrow {OD} = – \overrightarrow {OB} }\end{array}} \right.} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{OlatrungdiemAC}\\{OlatrungdiemBD}\end{array}} \right.\]
⇔ABCD là hình bình hành.
Ta có điều phải chứng minh.
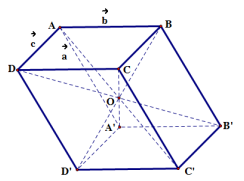
Bài 5. Cho hình hộp \[ABCD.A’B’C’D’\] tâm O. Chứng minh:
a) \[\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OA’} + \overrightarrow {OB’} + \overrightarrow {OC’} + \overrightarrow {OD’} = \overrightarrow 0 \]
b) Gọi D1, D2, D3 lần lượt là điểm đối xứng của điểm D’ qua A, B’, C. Chứng tỏ rằng \[\overrightarrow {B{D_1}} + \overrightarrow {B{D_2}} + \overrightarrow {B{D_3}} + \overrightarrow {BD’} = \overrightarrow 0 \].
Lời giải
a) Do O là trung điểm ba đoạn thẳng AC’, A’C, BD’, B’D nên ta có:
\[\overrightarrow {OA} + \overrightarrow {OC’} = \overrightarrow 0 ,\] \[\overrightarrow {OB} + \overrightarrow {OD} ‘ = \overrightarrow 0 \]
\[\overrightarrow {OC} + \overrightarrow {OA’} = \overrightarrow 0 ,\] \[\overrightarrow {OD} + \overrightarrow {OB} ‘ = \overrightarrow 0 \]
Cộng lại ta được điều phải chứng minh.
b) Đặt: \[\overrightarrow {AA’} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AD} = \overrightarrow c \]
Khi đó: \[\overrightarrow {B{D_1}} + \overrightarrow {B{D_2}} + \overrightarrow {B{D_3}} + \overrightarrow {BD’} = \left( {\overrightarrow {B{D_1}} + \overrightarrow {BD’} } \right) + \left( {\overrightarrow {B{D_2}} + \overrightarrow {B{D_3}} } \right)\]
Mà
\[\overrightarrow {B{D_1}} + \overrightarrow {BD’} = 2\overrightarrow {BA} = – 2\overrightarrow b \],
\[\overrightarrow {B{D_2}} = \overrightarrow {BB’} + \overrightarrow {B'{D_2}} = \overrightarrow a + ( – \overrightarrow c + \overrightarrow b )\],
\[\overrightarrow {B{D_3}} = \overrightarrow {BC} + \overrightarrow {C{D_3}} = \overrightarrow c – \overrightarrow a + \overrightarrow b \]
nên ta có:
\[\left( {\overrightarrow {B{D_1}} + \overrightarrow {BD’} } \right) + \left( {\overrightarrow {B{D_2}} + \overrightarrow {B{D_3}} } \right) = – 2\overrightarrow b + \overrightarrow a + ( – \overrightarrow c + \overrightarrow b ) + \overrightarrow c – \overrightarrow a + \overrightarrow b = \overrightarrow 0 \]
Dạng 2. Xác định vị trí các điểm thỏa điều kiện vectơ, chứng minh các điểm trùng nhau, các điểm thẳng hàng.
Phương pháp.
Thường đưa về các hệ thức quen thuộc liên quan đến các điểm như trung điểm đoạn thẳng, trọng tâm tam giác . . .
Lưu ý rằng:
\[\overrightarrow {AB} = \overrightarrow 0 \Leftrightarrow A \equiv B\].
Ba điểm A, B, C thẳng hàng ⇔ \[\overrightarrow {AB} \] và \[\overrightarrow {AC} \] cùng phương.
Khi gặp tổng hai vectơ cùng gốc ta thường dùng:
\[\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \]với I là trung điểm AB.
Khi gặp tổng ba vectơ cùng gốc ta thường dùng:
\[\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \] với G là trọng tâm tam giác ABC.
Bài 6. Cho tứ diện ABCD.
a) Xác định điểm O thỏa mãn \[\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \]. (1)
(Điểm O thỏa điều kiện trên gọi là trọng tâm của tứ diện ABCD).
b) Xác định điểm P để \[\left| {\overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {PC} + \overrightarrow {PD} } \right|\] có giá trị nhỏ nhất.
Lời giải
a) Gọi M và N lần lượt là trung điểm của AB và CD. Gọi I là trung điểm MN. Ta có:
\[\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = 2\overrightarrow {OM} + 2\overrightarrow {ON} = 2(\overrightarrow {OM} + \overrightarrow {ON} )\]
Vậy điểm O thỏa mãn (1) khi và chỉ khi:
\[\overrightarrow {OM} + \overrightarrow {ON} = \overrightarrow 0 \]⇔ \[2\overrightarrow {OI} = \overrightarrow 0 \] ⇔ O ≡ I.
Do đó O là trung điểm MN.
b) Gọi O là trọng tâm của tứ diện ABCD. Ta có:
\[\overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {PC} + \overrightarrow {PD} \]
\[ = \overrightarrow {PO} + \overrightarrow {OA} + \overrightarrow {PO} + \overrightarrow {OB} + \overrightarrow {PO} + \overrightarrow {OC} + \overrightarrow {PO} + \overrightarrow {OD} \]
\[ = 4\overrightarrow {PO} + \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = 4\overrightarrow {PO} \].
Do đó điều kiện cần và đủ để \[\left| {\overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {PC} + \overrightarrow {PD} } \right|\] đạt giá trị nhỏ nhất là:
\[\overrightarrow {PO} = \overrightarrow 0 \] ⇔ P ≡ O.
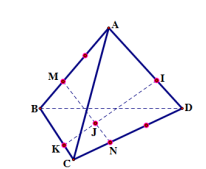
Bài 7. Cho tứ diện ABCD, M và N là hai điểm lần lượt thuộc AB và CD sao cho \[\overrightarrow {MA} = – 2\overrightarrow {MB} \], \[\overrightarrow {ND} = – 2\overrightarrow {NC} \]. Các điểm I, J, K lần lượt thuộc AD, MN, BC sao cho \[\overrightarrow {IA} = k\overrightarrow {ID} \], \[\overrightarrow {JM} = k\overrightarrow {JN} \], \[\overrightarrow {KB} = k\overrightarrow {KC} \] (k ≠ 1).
a) Biểu diễn \[\overrightarrow {IJ} \] theo \[\overrightarrow {AM} ,\overrightarrow {DN} \]; biểu diễn \[\overrightarrow {IK} \] theo \[\overrightarrow {MB} ,\overrightarrow {NC} \].
b) Chứng minh rằng các điểm I, J, K thẳng hàng.
Lời giải
a) Ta có:
\[\overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AM} + \overrightarrow {MJ} \]
\[\overrightarrow {IJ} = \overrightarrow {ID} + \overrightarrow {DN} + \overrightarrow {NJ} \]
\[k\overrightarrow {IJ} = k\overrightarrow {ID} + k\overrightarrow {DN} + k\overrightarrow {NJ} \]
\[k\overrightarrow {IJ} = \overrightarrow {IA} + k\overrightarrow {DN} + \overrightarrow {MJ} \]
\[(1 – k)\overrightarrow {IJ} = \overrightarrow {AM} – k\overrightarrow {DN} \]
Suy ra:
\[\overrightarrow {IJ} = \frac{1}{{1 – k}}\overrightarrow {AM} – \frac{k}{{1 – k}}\overrightarrow {DN} \]
Chứng minh tương tự như trên ta có:
\[\overrightarrow {JK} = \frac{1}{{1 – k}}\overrightarrow {MB} – \frac{k}{{1 – k}}\overrightarrow {NC} \]
Xem thêm