Phương pháp giải và bài tập về Cách xác định thiết diện của (α) với hình chóp khi biết (α) với một mặt phẳng (β) cho trước

Tài liệu Cách xác định thiết diện của (α) với hình chóp khi biết (α) với một mặt phẳng (β) cho trước gồm các nội dung chính sau:

Phương pháp

–          Tóm tắt lý thuyết ngắn gọn và phương pháp giải Cách xác định thiết diện của (α) với hình chóp khi biết (α) với một mặt phẳng (β) cho trước.

–          Gồm 3 bài tập tự luyện của các dạng bài tập Cách xác định thiết diện của (α) với hình chóp khi biết (α) với một mặt phẳng (β) cho trước có đáp án và lời giải chi tiết.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

DẠNG 7. CÁCH XÁC ĐỊNH THIẾT DIỆN CỦA (α) VỚI HÌNH CHÓP KHI BIẾT (α) VỚI MỘT MẶT PHẲNG (β) CHO TRƯỚC

 

Phương pháp:

–   Để xác định thiết diện trong trường hợp này ta sử dụng các tính chất sau.

–   Khi $\left(\alpha \right)\parallel \left(\beta \right)$ thì $\left(\alpha \right)$ sẽ song song với tất cả các đường thẳng trong $\left(\beta \right)$ và ta chuyển về dạng thiết diện song song với đường thẳng (§3)

Sử dụng $\left\{\begin{array}{l}\left(\alpha \right)\parallel \left(\beta \right)\\ \left(\beta \right)\parallel \left(\gamma \right)\\ \left(\beta \right)\cap \left(\gamma \right)=d\\ M\in \left(\alpha \right)\cap \left(\gamma \right)\end{array}\right.\Rightarrow \left(\alpha \right)\cap \left(\gamma \right)=d‘\parallel d,M\in d‘$.

–   Tìm đường thẳng $d$ mằn trong $\left(\beta \right)$ và xét các mặt phẳng có trong hình chóp mà chứa $d$, khi đó $\left(\alpha \right)\parallel d$ nên sẽ cắt các mặt phẳng chứa $d$ ( nếu có) theo các giao tuyến song song với $d$.

 

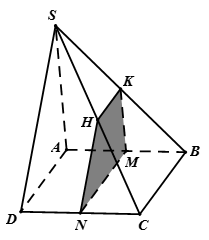
Câu 1: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành và $M,N$ lần lượt là trung điểm của $AB,CD$ . Xác định thiết diện của hình chóp cắt bởi $\left(\alpha \right)$ đi qua $MN$ và song song với mặt phẳng $\left(SAD\right)$.Thiết diện là hình gì?

     A. Tam giác                       B. Hình thang                    C. Hình bình hành             D. Tứ giác

Hướng dẫn giải::

Ta có $\left\{\begin{array}{l}M\in \left(SAB\right)\cap \left(\alpha \right)\\ \left(SAB\right)\cap \left(SAD\right)=SA\end{array}\right.$. $\Rightarrow \left(SAB\right)\cap \left(\alpha \right)=MK\parallel SA,K\in SB$ Tương tự  $\left\{\begin{array}{l}N\in \left(SCD\right)\cap \left(\alpha \right)\\ \left(\alpha \right)\parallel \left(SAD\right)\\ \left(SCD\right)\cap \left(SAD\right)=SD\end{array}\right.$. $\Rightarrow \left(SCD\right)\cap \left(\alpha \right)=NH\parallel SD,H\in SC$ Dễ thấy $HK=\left(\alpha \right)\cap \left(SBC\right)$. Thiết diện là tứ giác $MNHK$ Ba mặt phẳng $\left(ABCD\right),\left(SBC\right)$ và $\left(\alpha \right)$ đôi một cắt nhau theo các giao tuyến là $MN,HK,BC$, mà $MN\parallel BC\Rightarrow MN\parallel HK$. Vậy thiết diện là một hình thang.

 

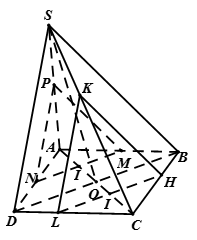
Câu 2: Cho hìh chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$ có $AC=a,BD=b$. Tam giác $SBD$ là tam giác đều. Một mặt phẳng $\left(\alpha \right)$ di động song song với mặt phẳng $\left(SBD\right)$ và đi qua điểm $I$ trên đoạn  $AC$ và $AI=x\left(0<x<a\right)$.

a) thiết diện của hình chóp cắt bởi $\left(\alpha \right)$ là hình gi?

     A. Tam giác                       B. Tứ giác                          C. Hình thang                    D. Hình bình hành

b) Tính diện tích thiết diện theo $a,b$ và $x$.

Hướng dẫn giải::

a) Trường hợp 1. Xét $I$ thuộc đoạn $OA$

Ta có $\left\{\begin{array}{l}I\in \left(\alpha \right)\cap \left(ABD\right)\\ \left(\alpha \right)\parallel \left(SBD\right)\\ \left(ABD\right)\cap \left(SBD\right)=BD\end{array}\right.$ $\Rightarrow \left(\alpha \right)\cap \left(ABD\right)=MN\parallel BD,I\in MN$. Tương tự  $\left\{\begin{array}{l}N\in \left(\alpha \right)\cap \left(SAD\right)\\ \left(\alpha \right)\parallel \left(SBD\right)\\ \left(SAD\right)\cap \left(SBD\right)=SD\end{array}\right.$. $\Rightarrow \left(SAD\right)\cap \left(\alpha \right)=NP\parallel SD,P\in SN$ Thiết diện là tam giác $MNP$.

 

Do $\left\{\begin{array}{l}\left(\alpha \right)\parallel \left(SBD\right)\\ \left(SAB\right)\cap \left(SBD\right)=SB\\ \left(SAB\right)\cap \left(\alpha \right)=MP\end{array}\right.\Rightarrow MP\parallel SB$. Hai tam giác $MNP$ và $BDS$ có các cặp cạnh tương ứng song song nên chúng đồng dạng, mà $BDS$ đều nên tam giác $MNP$ đều.

 

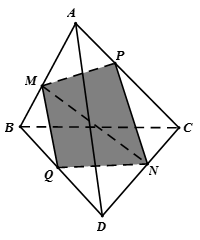
Trường hợp 2. Điểm $I$ thuộc đoạn $OC$, tương tự trường hợp 1 ta được thiết diện là tam giác đều $HKL$ như $\left(hv\right)$.

b) Trường hợp 1. $I$ thuộc đoạn $OA$

Ta có $S_{BCD}=\frac{B{D}^2\sqrt{3}}{4}=\frac{b^2\sqrt{3}}{4}$, Do $MN\parallel BD\Rightarrow \frac{MN}{BD}=\frac{AI}{AO}=\frac{2x}{a}$. $\Rightarrow S_{MNP}={\left(\frac{2x}{a}\right)}^2{S}_{BCD}=\frac{b^2{x}^2\sqrt{3}}{a^2}$ Trường hợp 2. $I$ thuộc đoạn $OC$, tính tương tự ta có $S_{MNP}={\left(\frac{HL}{BD}\right)}^2{S}_{BCD}={\text{[}\frac{2\left(a-x\right)}{a}\text{]}}^2\frac{b^2\sqrt{3}}{4}=\frac{b^2{\left(a-x\right)}^2\sqrt{3}}{a^2}$. Vậy $S_{td}=\left\{\begin{array}{l}\frac{b^2{x}^2\sqrt{3}}{a^2};I\in \left(OA\right)\\ \frac{b^2{\left(a-x\right)}^2\sqrt{3}}{a^2};I\in \left(OC\right)\end{array}\right.$.

Xem thêm