Phương pháp giải và bài tập về Cách chứng minh hai đường thẳng vuông góc

Tài liệu Cách chứng minh hai đường thẳng vuông góc gồm các nội dung chính sau:

I. Phương phương giải

– Tóm tắt lý thuyết ngắn gọn Hai đường thẳng vuông góc.

II. Bài tập

– Gồm 14 bài tập tự luyện có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng bài tập Cách chứng minh hai đường thẳng vuông góc.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Cách chứng minh hai đường thẳng vuông góc (ảnh 1)

DẠNG 4. CÁCH CHỨNG MINH HAI ĐƯỜNG THẲNG VUÔNG GÓC

I. PHƯƠNG PHÁP:

Để chứng minh $d_{1} ⊥ d_{2}$ ta có trong phần này ta có thể thực hiện theo các cách sau:

· Chứng minh $d_{1} ⊥ d_{2}$ ta chứng minh $\vec{u_{1}} \vec{u_{2}} = 0$ trong đó $\vec{u_{1}}, \vec{u_{2}}$ lần lượt là các vec tơ chỉ phương của $d_{1}$ và $d_{2}$ .

· Sử dụng tính chất $\{\begin{cases} b ∥ c \\ a ⊥ c \end{cases} \Rightarrow a ⊥ b$ .

· Sử dụng định lí Pitago hoặc xác định góc giữa $d_{1}, d_{2}$ và tính trực tiếp góc đó.

· Tính độ dài đoạn thẳng, diện tích của một đa giác

· Tính tích vô hướng…

II. BÀI TẬP

Câu 1: Cho hình hộp $A B C D . A^{‘} B^{‘} C^{‘} D^{‘}$ có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh đề nào có thể sai?

A. $A^{‘} C^{‘} ⊥ B D$ . B. $B B^{‘} ⊥ B D$ . C. $A^{‘} B ⊥ D C^{‘}$ . D. $B C^{‘} ⊥ A^{‘} D$ .

Hướng dẫn giải:

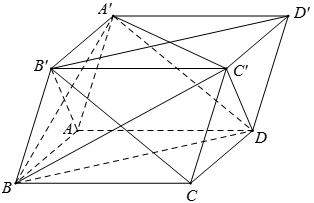
Chọn B.

Chú ý: Hình hộp có tất cả các cạnh bằng nhau còn gọi là hình hộp thoi.

A đúng vì:

$\{\begin{cases} A^{‘} C^{‘} ⊥ B^{‘} D^{‘} \\ B^{‘} D^{‘} // B D \end{cases} \Rightarrow A^{‘} C^{‘} ⊥ B D$ .

B sai vì:

C đúng vì: $\{\begin{cases} A^{‘} B ⊥ A B^{‘} \\ A B^{‘} // D C^{‘} \end{cases} \Rightarrow A^{‘} B ⊥ D C^{‘}$ .

D đúng vì: $\{\begin{cases} B C^{‘} ⊥ B^{‘} C \\ B^{‘} C // A^{‘} D \end{cases} \Rightarrow B C^{‘} ⊥ A^{‘} D$

Câu 2: Cho tứ diện $A B C D$ . Chứng minh rằng nếu $\vec{A B} . \vec{A C} = \vec{A C} . \vec{A D} = \vec{A D} . \vec{A B}$ thì $A B ⊥ C D$ , $A C ⊥ B D$ , $A D ⊥ B C$ . Điều ngược lại đúng không?

Sau đây là lời giải:

Bước 1: $\vec{A B} . \vec{A C} = \vec{A C} . \vec{A D}$ $\Leftrightarrow$ $\vec{A C} . (\vec{A B} - \vec{A D}) = 0$ . $\Leftrightarrow$ $\vec{A C} . \vec{D B} = 0$ $\Leftrightarrow$ $A C ⊥ B D$

Bước 2: Chứng minh tương tự, từ $\vec{A C} . \vec{A D} = \vec{A D} . \vec{A B}$ ta được $A D ⊥ B C$ và $\vec{A B} . \vec{A C} = \vec{A D} . \vec{A B}$ ta được .

Bước 3: Ngược lại đúng, vì quá trình chứng minh ở bước 1 và 2 là quá trình biến đổi tương đương.

Bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?

A. Đúng. B. Sai từ bước 1. C. Sai từ bước 1. D. Sai ở bước 3.

Hướng dẫn giải:

Chọn A.

Câu 4: Cho tứ diện $A B C D$ có $A B$ vuông góc với $C D$ . Mặt phẳng $(P)$ song song với $A B$ và $C D$ lần lượt cắt $B C, D B, A D, A C$ tại $M, N, P, Q$ . Tứ giác $M N P Q$ là hình gì?

A. Hình thang. B. Hình bình hành.

C. Hình chữ nhật. D. Tứ giác không phải là hình thang.

Hướng dẫn giải:

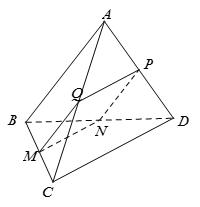
Chọn C.

Ta có: $\{\begin{cases} (M N P Q) // A B \\ (M N P Q) \cap (A B C) = M Q \end{cases} \Rightarrow M Q // A B .$

Tương tự ta có: $M N // C D, N P // A B, Q P // C D$ .

Do đó tứ giác $M N P Q$ là hình bình hành

lại có $M N ⊥ M Q (d o A B ⊥ C D)$ .

Vậy tứ giác $M N P Q$ là hình chữ nhật.

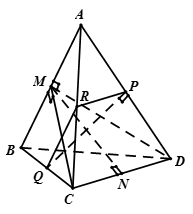
Câu 5: Cho tứ diện đều $A B C D$ có cạnh bằng $a$ . Gọi $M, N, P, Q, R$ lần lượt là trung điểm của $A B, C D, A D, B C$ và $A C$ .

a) Khẳng định nào sau đây là đúng nhất?

A. $M N ⊥ R P, M N ⊥ R Q$ B. $M N ⊥ R P,$ MN cắt RQ

C. MN chéo RP; MN chéo RQ D. Cả A, B, C đều sai

b) Tính góc của hai đường thẳng AB và CD?

A. $\hat{(A B, C D)} = 60^{0}$ B. $\hat{(A B, C D)} = 30^{0}$

C. $\hat{(A B, C D)} = 45^{0}$ D. $\hat{(A B, C D)} = 90^{0}$

Hướng dẫn giải:

a) Ta có $M C = M D = \frac{a \sqrt{3}}{2}$ nên tam giác $M C D$ cân tại $M$ , do đó $M N ⊥ C D$ .

Lại có $R P ∥ C D \Rightarrow M N ⊥ R Q$ .

b) Tương tự ta có $Q P ⊥ A D$

Trong tam giác vuông $P D Q$ ta có

$Q P^{2} = Q D^{2} - D P^{2} = {(\frac{a \sqrt{3}}{2})}^{2} - {(\frac{a}{2})}^{2} = \frac{a^{2}}{2}$ Ta có : $R Q^{2} + R P^{2} = {(\frac{a}{2})}^{2} + {(\frac{a}{2})}^{2} = a^{2} = Q P^{2}$

Do đó tam giác $R P Q$ vuông tại $R$ , hay $R P ⊥ R Q$ .

Vì vậy $\{\begin{cases} A B ∥ R Q \\ C D ∥ R P \\ R P ⊥ R Q \end{cases} \Rightarrow A B ⊥ C D$ .

Xem thêm

Bài liên quan:

Leave a Comment Hủy