Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Phân dạng bài tập và phương pháp giải bài toán về khoảng cách từ điểm đến mặt phẳng
PHẦN 1: KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG DẠNG 1: DỰNG HÌNH CHIẾU VÀ TÍNH KHOẢNG CÁCH
*) Quy trình tìm hình chiếu của O trên mặt phẳng (α)
Bước 1: Tìm một mặt phẳng (P) ^ d với d là đường thẳng nằm trong (a).
Bước 2: Tìm D = (P) Ç (a)
Bước 3: Từ O kẻ OH ^ D thì H là hình chiếu của O trên (a) . Khi đó, d(O;(α)) = OH
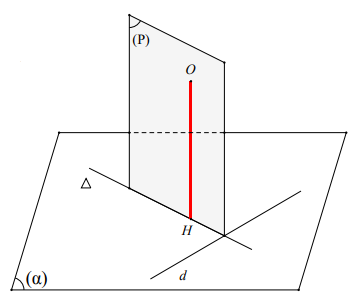
*) Tính OH Dùng công thức diện tích, các hệ thức lượng trong tam giác, tam giác đồng dạng để tính OH Với mỗi dạng bài ta lại có quy trình dựng cụ thể hơn mà chúng ta sẽ tìm hiểu dưới đây
Dạng 1.1. Khoảng cách từ O đến (α) chứa đường cao hình chóp
*) Dựng hình chiếu OH
Bước 1: D = (a) Ç đáy
Bước 2: Kẻ OH ^ D .
Chứng minh OH ^ (a) Þ d(O; (a)) = OH
*) Tính OH Dạng này thường tính qua diện tích tam giác.
B – VÍ DỤ
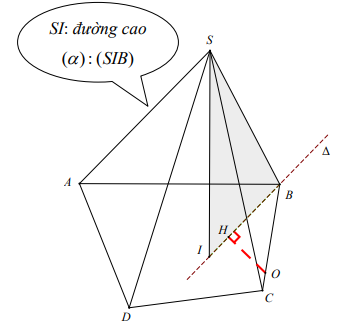
Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = 2a; BC \[\frac{{3a}}{2}\]AD =3a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trung điểm I của BD. Tính khoảng cách từ C đến mặt phẳng (SBD).
Giải:
*) Dựng hình chiếu CH Kẻ CH ^ BD,(H Î BD)
Ta có: SI ^ (ABC) Þ SI ^ CH (1)
Mà, CH ^ BD (2)
Từ (1) và (2) suy ra, CH ^ SB Þ d(C;(SBD)) = CH
*) Tính CH
Ta tính CH qua diện tích tam giác BCD.
SDBCD = \[\frac{1}{2}\]AB.BC = \[\frac{1}{2}\]BD.CH Þ CH = \[\frac{{AB.BC}}{{BD}}\]
\[\begin{array}{l}BD = \sqrt {A{B^2} + A{{\rm{D}}^2}} = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {3a} \right)}^2}} = \sqrt {13{a^2}} = a\sqrt {13} ;\\BC = \frac{{3a}}{2}\end{array}\]
Þ CH = \[\frac{{2a.\frac{{3a}}{2}}}{{a\sqrt {13} }} = \frac{{3a}}{{\sqrt {13} }}\]
Vậy, d(C;(SBD)) = \[\frac{{3a}}{{\sqrt {13} }}\]
C – BÀI TẬP LUYỆN TẬP
Bài 1 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a. M là trung điểm của CD, hình chiếu vuông góc của S lên (ABCD) là trung điểm H của AM. Biết góc giữa SD và (ABCD) bằng 600 . Tính khoảng cách
a. Từ B đến (SAM)
b. Từ C đến (SAH).
Bài 2: Cho hình chóp S.ABC có đáy là tam giác vuông tại A với AB = \[a\sqrt 3 \] ; AC = a. Gọi I là điểm trên BC sao cho BI = \[\frac{1}{2}\] IC và H là trung điểm của AI. Biết rằng SH ^ (ABC) và góc giữa mặt phẳng (SBC) và (ABC) bằng 600 . Tính khoảng cách:
a. Từ B đến (SHC)
b. Từ C đến (SAI).
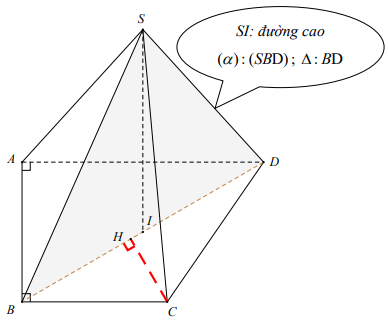
Dạng 2 : Khoảng cách từ O chân đƣờng cao đến mặt phẳng (α) chứa cạnh trong mặt đáy
A – KIẾN THỨC CHUNG
*) Dựng hình chiếu OH
Bước 1 : Dựng mặt phẳng (P) qua O và vuông góc với CD bằng cách kẻ từ S hoặc từ O đường vuông góc với CD. Khi đó, (P) là (SOM)
Bước 2 : D = (SOM ) Ç (SCD)
Chứng minh OH ^ (a) Þ d(O;(a)) = OH
*) Tính OH
Dạng này thường dùng hệ thức lượng trong tam giác vuông
B – VÍ DỤ
Ví dụ 1 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a. Mặt bên (SAB) nằm trong mặt phẳng vuông góc với đáy, hình chiếu vuông góc của S trên mặt đáy là điểm H thuộc đoạn AB sao cho BH = 2AH. Góc giữa SC và mặt phẳng đáy là 600 . Tính khoảng cách từ điểm H đến mặt phẳng (SCD).
Giải :
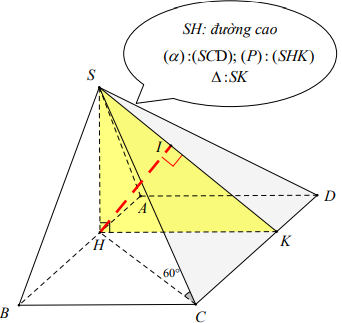
*) Dựng hình chiếu HI
Kẻ HK ^ CD (KÎCD)
Ta có : SH ^ (ABCD) Þ SH ^ CD
Mà HK ^ CDÞ (SHK) ^ CD
Kẻ HI ^ SK (I Î HK) (1) CD ^ (SHK)
Þ CD ^ HI (2)
Từ (1) và (2) suy ra HI ^ (SCD)
Þ d(H;(SCD) = HI
*) Tính HI
Ta có : BH = 2AH Þ BH = \[\frac{2}{3}a\]Þ CH = \[\frac{{a\sqrt {13} }}{3}\]
SH = \[\frac{{a\sqrt {39} }}{3}\].
Ta có: \[\frac{1}{{H{I^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{S{K^2}}} \Rightarrow HI = \frac{{a\sqrt {13} }}{4}\]
Vậy d(H,(SCD)) = \[\frac{{a\sqrt {13} }}{4}\]
C – BÀI TẬP LUYỆN TẬP
Bài 1: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Gọi I là trung điểm của cạnh AB. HÌnh chiếu vuông góc của đỉnh S trên mặt phẳng đáy là trung điểm H của CI, góc giữa đường thẳng SA và mặt đáy bằng 600 . Tính khoảng cách từ điểm H đến mặt phẳng (SBC).
Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Biết SA ^ (ABCD) , SC hợp với mặt phẳng ( ABCD) một góc a với tan a = \[\frac{4}{5}\], AB=3a, BC=4a. Tính khoảng cách từ điểm A đến mặt phẳng (SBC).
Bài 3: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I và có cạnh bằng a, BAD = 60o. Gọi H là trung điểm của IB và SH vuông góc với mặt phẳng (ABCD). Góc giữa SC và mặt phẳng (ABCD) bằng 45 . Tính khoảng cách từ điểm H đến mặt phẳng (SCD).
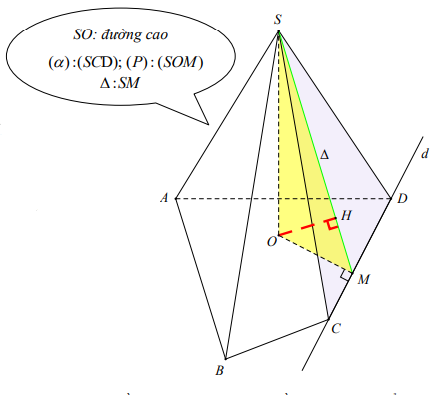
DẠNG 2 : DỜI ĐIỂM VÀ DỰNG KHOẢNG CÁCH GIÁN TIẾP
A – KIẾN THỨC CHUNG
Trong một số trường hợp việc dựng khoảng cách trực tiếp từ O trở nên khó khăn. Do đó, ta có thể dùng tính chất về tỉ số khoảng cách để dời khoảng cách từ O về khoảng cách từ điểm M đơn giản hơn (về dạng 1.1 và 1.2 ở trên). Cụ thể :
*) Tính chất
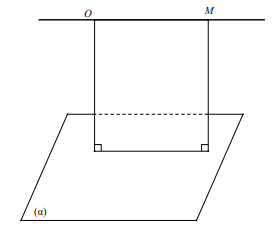
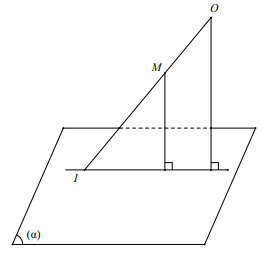
– Nếu OM cắt mặt phẳng (a ) tại I thì ta có :
\[\frac{{d(O;\left( \alpha \right))}}{{d(M;\left( \alpha \right))}} = \frac{{OI}}{{MI}}\]
– Nếu OM / / (a ) thì \[d(O;\left( \alpha \right)) = d(M;\left( \alpha \right))\]
*) Chú ý : Một số bài phức tạp có thể phải dời đến 2 lần để việc tính tỉ số đơn giản hơn
B – VÍ DỤ
Ví dụ 1 : Cho hình chóp tứ giác S.ABCD, đáy ABCD là hình chữ nhật với AB =a, AD = \[a\sqrt 3 \] , hình chiếu vuông góc của S lên (ABCD) là trung điểm H của OB với O là tâm đáy. Biết góc giữa SC và mặt phẳng (ABCD) bằng 600. Tính khoảng cách từ B đến (SAC).
Giải :
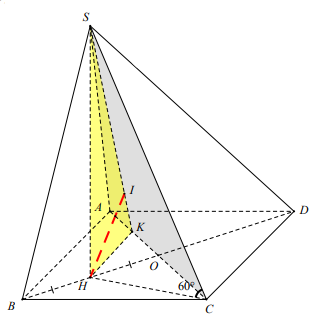
Thay vì dựng khoảng cách từ B đến (SAC) ta sẽ dựng khoảng cách từ H đến (SAC) (theo dạng 1.2) ư
*) Dựng khoảng cách HI Kẻ HK ^ AC (K Î AC)
Ta có : SH ^ (ABCD) Þ SH ^ AC
Mà HK ^ AC Þ (SHK) ^ AC
Kẻ HI ^ SK (I ÎHK) (1)
AC ^ (SHK) Þ AC ^ HI (2)
Từ (1) và (2) suy ra HI ^ (SAC) Þ d(H; (SAC)) = HI
*) Tính HI Theo công thức trung tuyến tính được :
HC2 = \[\frac{{C{O^2} + B{C^2}}}{2} – \frac{{O{B^2}}}{4} = \frac{{7{a^2}}}{4}\]
\[ \Rightarrow HC = \frac{{a\sqrt 7 }}{2} \Rightarrow SH = \frac{{a\sqrt {21} }}{2}\]
Kẻ BM ^ AC (MÎ AC) Þ BM = \[\frac{{a\sqrt 3 }}{2}\]
Þ HK = \[\frac{{a\sqrt 3 }}{4}\]
\[\frac{1}{{H{I^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{S{K^2}}} = \frac{{128}}{{21{a^2}}} \Rightarrow HI = \frac{{a\sqrt {42} }}{{16}}\]
d(H;(SAC)) =\[\frac{{a\sqrt {42} }}{{16}}\]
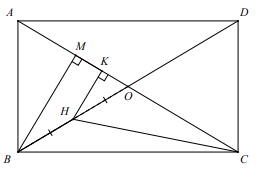
*) Tính khoảng cách từ B
Ta có : BH \[ \cap \](SAC) = O
\[ \Rightarrow \] \[\frac{{d(B;(SAC))}}{{d(H;(SAC))}} = \frac{{BO}}{{HO}} = 2\]
\[ \Rightarrow d(B;(SAC)) = 2d(H;(SAC)) = \frac{{a\sqrt {42} }}{8}\]
Vậy d(B;(SAC)) = \[\frac{{a\sqrt {42} }}{8}\]
Xem thêm