Lý thuyết Góc lượng giác. Giá trị lượng giác của góc lượng giác (Cánh diều 2023) hay, chi tiết | Toán lớp 11

Lý thuyết Toán lớp 11 Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác

A. Lý thuyết Góc lượng giác. Giá trị lượng giác của góc lượng giác

I. Góc lượng giác

1. Góc hình học và số đo của chúng

 

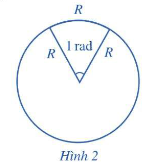
*Nhận xét:

– Đơn vị đo góc: độ hoặc radian (rad).

– Ta có: ${180}^o=\pi$rad, do đó 1 rad $={\left(\frac{180}{\pi }\right)}^o$, $1^o=\left(\frac{\pi }{180}\right)$rad.

– Người ta thường không viết chữ radian hay rad sau số đo góc.

VD: $\frac{\pi }{2}$rad cũng được viết là $\frac{\pi }{2}$.

2. Góc lượng giác và số đo của chúng

a, Khái niệm

– Cho 2 tia Ou, Ov. Nếu tia Om quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ Ou đến trùng với tia Ov thì ta nói: Tia Om quét một góc lượng giác với tia đầu Ou và tia cuối Ov.

Kí hiệu: (Ou, Ov).

– Mỗi góc lượng giác được xác định bởi tia đầu Ou, tia cuối Ov và số đo của góc đó.

b, Tính chất

– Cho hai góc lượng giác = và (O’u’,O’v’) có tia đầu trùng nhau $\left(Ou\equiv O^{\prime }{u}^{\prime }\right)$, tia cuối trùng nhau $\left(Ov\equiv O^{\prime }{v}^{\prime }\right)$.

Khi đó, nếu sử dụng đợn vị đo là độ thì ta có:

$\left(Ou,Ov\right)=\left(O^{\prime }{u}^{\prime },O^{\prime }{v}^{\prime }\right)+k{360}^o,k\in \mathbb{Z}.$

Nếu sử dụng đơn vị đo là radian thì:

$\left(Ou,Ov\right)=\left(O^{\prime }{u}^{\prime },O^{\prime }{v}^{\prime }\right)+k2\pi ,k\in \mathbb{Z}.$

* Hệ thức Chasles

Với 3 tia Ou, Ov, Ow bất kì ta có:

 (Ou,Ov) + (Ov, Ow) = (Ou,Ow) $+k2\pi ,k\in \mathbb{Z}.$

II. Giá trị lượng giác của góc lượng giác

1. Đường tròn lượng giác

Trong mặt phẳng toa độ đã được định hướng Oxy, lấy điểm A(1;0). Đường tròn tâm O, bán kính OA = 1 được gọi là đường tròn lượng giác (hay đường tròn đơn vị) gốc A.

2. Giá trị lượng giác của góc lượng giác

 

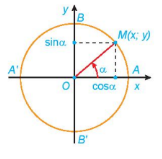
– Trục tung là trục sin, trục hoành là trục côsin.

– Điểm M(x;y) nằm trên đường tròn như hình vẽ. Khi đó:

$x=$cos$\alpha$, $y=$sin$\alpha$.

tan$\alpha$$=\frac{\sin \alpha }{\cos \alpha }=\frac{y}{x}\left(x\ne 0\right)$

$\cot \alpha =\frac{\cos \alpha }{\sin \alpha }=\frac{x}{y}\left(y\ne 0\right)$

* Dấu của các giá trị lượng giác của góc $\alpha$

 

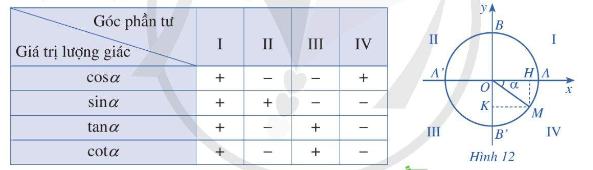
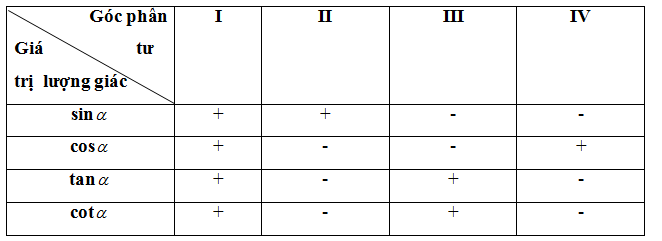
* Các công thức lượng giác cơ bản

$\begin{array}{l}{\sin }^2\alpha +{\cos }^2\alpha =1\\ 1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha }\left(\alpha \ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\right)\\ 1+{\cot }^2\alpha =\frac{1}{{\sin }^2\alpha }\left(\alpha \ne k\pi ,k\in \mathbb{Z}\right)\\ \tan \alpha .\cot \alpha =1\left(\alpha \ne \frac{k\pi }{2},k\in \mathbb{Z}\right)\end{array}$

3. Giá trị lượng giác của các góc có liên quan đặc biệt

• Hai góc đối nhau $\alpha$ và $-\alpha$

$\begin{array}{l}\sin \left(-\alpha \right)=-\sin \alpha \\ \cos \left(-\alpha \right)=\cos \alpha \\ \tan \left(-\alpha \right)=-\tan \alpha \\ \cot \left(-\alpha \right)=-\cot \alpha \end{array}$

• Hai góc bù nhau ($\alpha$ và $\pi$–$\alpha$)

$\begin{array}{l}\sin \left(\pi -\alpha \right)=\sin \alpha \\ \cos \left(\pi -\alpha \right)=-\cos \alpha \\ \tan \left(\pi -\alpha \right)=-\tan \alpha \\ \cot \left(\pi -\alpha \right)=-\cot \alpha \end{array}$

• Hai góc phụ nhau ($\alpha$ và $\frac{\pi }{2}$–$\alpha$)

$\begin{array}{l}\sin \left(\frac{\pi }{2}-\alpha \right)=c\mathrm{o}\mathrm{s}\alpha \\ \cos \left(\frac{\pi }{2}-\alpha \right)=\sin \alpha \\ \tan \left(\frac{\pi }{2}-\alpha \right)=\cot \alpha \\ \cot \left(\frac{\pi }{2}-\alpha \right)=\tan \alpha \end{array}$

• Hai góc hơn kém $\pi$($\alpha$ và $\pi$ + $\alpha$)

$\begin{array}{l}\sin \left(\pi +\alpha \right)=-\sin \alpha \\ \cos \left(\pi +\alpha \right)=-\cos \alpha \\ \tan \left(\pi +\alpha \right)=\tan \alpha \\ \cot \left(\pi +\alpha \right)=\cot \alpha \end{array}$

4. Sử dụng máy tính cầm tay để tính giá trị của một góc lượng giác

Đơn vị độ:

 

Đơn vị radian:

 

 

B. Bài tập Góc lượng giác. Giá trị lượng giác của góc lượng giác

Bài 1. Tìm các giá trị lượng giác của góc lượng giác $\alpha =\frac{3\pi }{4}$.

Hướng dẫn giải

Lấy điểm M trên đường tròn lượng giác sao cho $\left(OA,OM\right)=\alpha =\frac{3\pi }{4}$ (hình vẽ).

Gọi H, K lần lượt là hình chiếu của điểm M lên các trục Ox, Oy.

Khi đó $\widehat{AOM}=\frac{3\pi }{4}$.

Suy ra $\widehat{BOM}=\widehat{KOM}=\frac{3\pi }{4}-\frac{\pi }{2}=\frac{\pi }{4}$.

Tam giác KOM vuông tại K, có:

⦁ $OK=OM.\cos \widehat{KOM}=1.\cos \frac{\pi }{4}=\frac{\sqrt{2}}{2}$;

⦁ $MK=OM.\sin \widehat{KOM}=1.\sin \frac{\pi }{4}=\frac{\sqrt{2}}{2}$.

Suy ra tọa độ .

Vậy $\sin \frac{3\pi }{4}=-\frac{\sqrt{2}}{2}$; $\cos \frac{3\pi }{4}=\frac{\sqrt{2}}{2}$; $\tan \frac{3\pi }{4}=\frac{\sin \frac{3\pi }{4}}{\cos \frac{3\pi }{4}}=-1$ và $\cot \frac{3\pi }{4}=\frac{\cos \frac{3\pi }{4}}{\sin \frac{3\pi }{4}}=-1$.

Bài 2. Tìm số đo α của góc lượng giác (Ou, Ov) với 0 ≤ α ≤ 2π (0° ≤ α ≤ 360°), biết một góc lượng giác có cùng tia đầu, tia cuối với góc đó có số đo là:

a) $\frac{33\pi }{4}$;

b) $-\frac{291983\pi }{3}$;

c) 3270°.

Hướng dẫn giải

a) Ta có: .

Vì 0 ≤ α ≤ 2π nên $0\le \frac{33\pi }{4}+k2\pi \le 2\pi$.

$\iff -\frac{33\pi }{4}\le k2\pi \le -\frac{25\pi }{4}$.

$\iff -\frac{33}{8}\le k\le -\frac{25}{8}$.

Mà k ∈ ℤ, suy ra k = –4.

Vậy .

b) Ta có: .

Vì 0 ≤ α ≤ 2π nên $0\le -\frac{291983\pi }{3}+k2\pi \le 2\pi$.

$\iff \frac{291983\pi }{3}\le k2\pi \le \frac{291989\pi }{3}$.

$\iff \frac{291983}{6}\le k\le \frac{291989}{6}$.

Mà k ∈ ℤ, suy ra k = 48664.

Vậy $\alpha =-\frac{291983\pi }{3}+48664.2\pi =\frac{\pi }{3}$.

c) Ta có: (Ou,Ov) = α = 3270° + k.360° (k ∈ ℤ).

Vì 0° ≤ α ≤ 360° nên 0° ≤ 3270° + k.360° ≤  360°.

⇔ –3270° ≤ k.360° ≤  –2910°.

$\iff -\frac{109}{12}\le k\le -\frac{97}{12}$.

Mà k ∈ ℤ, suy ra k = –9.

Vậy α = 3270° + (–9).360° = 30°.

Bài 3.

a) Cho $\cos x=\frac{2}{3}$. Tính $A=\frac{\tan x+3\cot x}{\tan x+\cot x}$.

b) Cho $\sin x=-\frac{4}{5}$ và $\frac{3\pi }{2}<x<2\pi$. Tính $B=\frac{\sin x+3\cos x}{\tan x}$.

c) Cho tanx = 3. Tính $C=\frac{\sin x-\cos x}{{\sin }^{3}x+3{\cos }^{3}x+2\sin x}$.

Hướng dẫn giải

a) Ta có $A=\frac{\tan x+3\cot x}{\tan x+\cot x}=\frac{\tan x+3.\frac{1}{\tan x}}{\tan x+\frac{1}{\tan x}}$ (do cosx ≠ 0)

                 

b) Vì $\frac{3\pi }{2}<x<2\pi$ nên cosx > 0.

Ta có sin²x + cos²x = 1, suy ra

.

$\iff \cos x=\frac{3}{5}$ (do cosx > 0).

Suy ra $\tan x=\frac{\sin x}{\cos x}=-\frac{4}{5}:\frac{3}{5}=-\frac{4}{3}$.

Khi đó $B=\frac{\sin x+3\cos x}{\tan x}=\frac{-\frac{4}{5}+3.\frac{3}{5}}{-\frac{4}{3}}=-\frac{3}{4}$.

c) Do tanx = 3 nên cosx ≠ 0.

Chia cả tử và mẫu của C cho cos³x, ta được:

$C=\frac{\frac{\sin x}{{\cos }^{3}x}-\frac{\cos x}{{\cos }^{3}x}}{\frac{{\sin }^{3}x}{{\cos }^{3}x}+3+2.\frac{\sin x}{{\cos }^{3}x}}$

Bài 4. Cho tam giác ABC. Chứng minh rằng:

Hướng dẫn giải

Tam giác ABC, có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$

Suy ra $\widehat{A}+2\widehat{B}+\widehat{C}=180°+\widehat{B}$ và $\widehat{B}+\widehat{C}=180°-\widehat{A}$.

 

VP = tanA.cot(B + C) = tanA.cot(180° – A) = tanA.(–cotA) = –tanA.cotA = –1 .

Khi đó VT = VP (= –1).

Vậy ta có điều phải chứng minh.

Bài 5. Một bánh xe có bán kính R = 2,4 m quay một góc bằng 30°. Tính độ dài đường đi của một điểm bất kì trên vành bánh xe.

Hướng dẫn giải

Ta xem vành bánh xe là một đường tròn có bán kính R = 2,4 m.

Độ dài đường đi của một điểm bất kì trên vành bánh xe là độ dài của cung tròn có số đo 30°.

Vậy độ dài đường đi cần tìm là $\frac{30°.2\pi .R}{360°}=\frac{30°.2\pi \mathrm{.2,4}}{360°}=\mathrm{0,4}$ m.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác

Lý thuyết Bài 2: Các phép biến đổi lượng giác

Lý thuyết Bài 3: Hàm số lượng giác và đồ thị

Lý thuyết Bài 4: Phương trình lượng giác cơ bản

Lý thuyết Bài 1: Dãy số

Lý thuyết Bài 2: Cấp số cộng

Xem thêm các bài tóm tắt lý thuyết chương Toán lớp 11 Cánh diều hay, chi tiết khác:

Lý thuyết Chương 1: Hàm số lượng giác và phương trình lượng giác

Lý thuyết Chương 2: Dãy số. Cấp số cộng. Cấp số nhân

Lý thuyết Chương 3: Giới hạn. Hàm số liên tục

Lý thuyết Chương 4: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song