Lý thuyết Dãy số (Chân trời sáng tạo 2023) hay, chi tiết | Toán lớp 11

Lý thuyết Toán lớp 11 Bài 1: Dãy số

A. Lý thuyết Dãy số

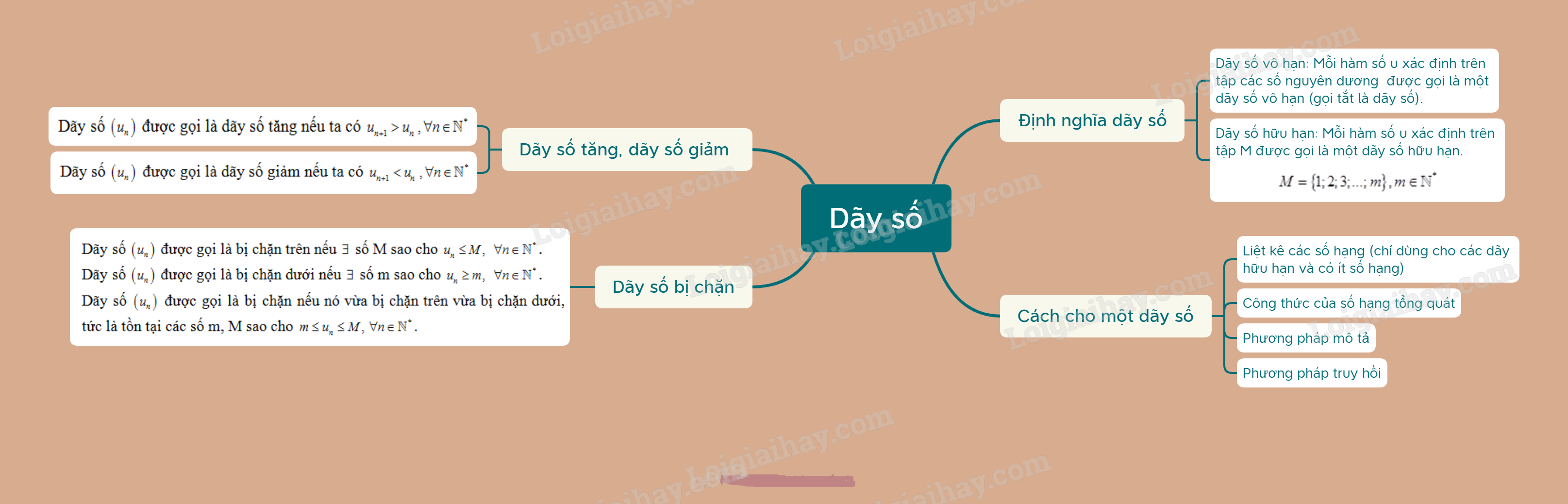
1. Định nghĩa dãy số

• Dãy số vô hạn

– Hàm số u xác định trên tập các số nguyên dương ${\mathbb{N}}^{\ast }$được gọi là một dãy số vô hạn (gọi tắt là dãy số), nghĩa là

$u:{\mathbb{N}}^{\ast }\to \mathbb{R}$

$n\mapsto u_n=u\left(n\right)$

  Dãy số trên được kí hiệu là $\left(u_n\right)$.

– Dãy số $\left(u_n\right)$được viết dưới dạng khai triển $u_1,u_2,u_3,...,u_n,...$

– Số $u_1$ là số hạng đầu; $u_n$là số hạng thứ n và gọi là số hạng tổng quát của dãy số.

*Chú ý: Nếu $\mathrm{\forall }n\in {\mathbb{N}}^{\ast },u_n=c$thì $\left(u_n\right)$được gọi là dãy số không đổi.

• Dãy số hữu hạn

Mỗi hàm số u xác định trên tập $M=\left\{1;2;3;...;m\right\},m\in {\mathbb{N}}^{\ast }$ được gọi là một dãy số hữu hạn.Dạng khai triển của dãy số hữu hạn là $u_1,u_2,u_3,...,u_m$.

Trong đó, số $u_1$ gọi là số hạng đầu, $u_m$là số hạng cuối.

2. Cách cho một dãy số

Một dãy số có thể cho bằng:

– Liệt kê các số hạng (với các dãy hữu hạn).

– Công thức của số hạng tổng quát $u_n$.

– Phương pháp truy hồi:

+) Cho số hạng thứ nhất $u_1$ (hoặc một vài số hạng đầu tiên)

+) Cho một công thức tính $u_n$ theo$u_{n-1}$ (hoặc theo vài số hạng đứng ngay trước nó).

– Phương pháp mô tả.

3. Dãy số tăng, dãy số giảm

Dãy số $\left(u_n\right)$ được gọi là dãy số tăng nếu ta có $u_{n+1}>u_n$$,\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là dãy số giảm nếu ta có $u_{n+1}<u_n$$,\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

4. Dãy số bị chặn

Dãy số $\left(u_n\right)$ được gọi là bị chặn trên nếu $\mathrm{\exists }$ số M sao cho $u_n\le M,$ $\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là bị chặn dưới nếu $\mathrm{\exists }$ số m sao cho $u_n\ge m,$ $\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho $m\le u_n\le M,$$\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

 

 

B. Bài tập Dãy số

Bài 1. Cho dãy số (u_n) được xác định bởi $u_n=\frac{n+1}{2^n}$ với n ∈ ℕ*.

a) Liệt kê 3 số hạng đầu của dãy số (u_n).

b) Xét tính tăng, giảm của dãy số (u_n).

Hướng dẫn giải

a) Ta có: $u_1=\frac{1+1}{2^1}=1,u_2=\frac{2+1}{2^2}=\frac{3}{4},u_3=\frac{3+1}{2^3}=\frac{1}{2}.$

b) Ta có: $u_{n+1}-u_n=\frac{\left(n+1\right)+1}{2^{n+1}}-\frac{n+1}{2^n}$

$=\frac{n+2}{{2.2}^n}-\frac{n+1}{2^n}=\frac{n+2-2n-2}{{2.2}^n}=\frac{-n}{2^{n+1}}<0$

⇔ u_{n + 1} < u_n.

Vậy (u_n) là dãy số giảm.

Bài 2. Xét tính bị chặn của dãy số sau: u_n = 4 – 3n – n².

Hướng dẫn giải

Ta có: u_{n + 1} – u_n = 4 – 3(n + 1) – (n + 1)² – (4 – 3n – n²)

= 4 – 3n – 3 – n² – 2n – 1 – 4 + 3n + n²

= − 2n − 4

⇔ u_{n + 1} < u_n.

⇒ (u_n) là dãy số giảm, tức là n càng tăng thì u_n càng giảm ⇒ (u_n) không bị chặn dưới.

Vậy (u_n) là dãy số bị chặn trên.

Bài 3. Cho dãy số (u_n) bởi hệ thức truy hồi: $u_1=\frac{1}{2},u_{n+1}=2u_n.$ Tìm ra công thức số hạng tổng quát của dãy số này.

Hướng dẫn giải

Ta có: $u_1=\frac{1}{2}=2^{-1};u_2=1=2^0;u_3=2=2^1;u_4=4=2^2.$

Ta nhận thấy u₁ = 2^{1 – 2}; u₂ = 2^{2 – 2}; u₃ = 2^{3 – 2}; u₄ = 2^{4 – 2}.

Vậy công thức số hạng tổng quát của dãy số (u_n) là u_n = 2^{n – 2}.

Bài 4. Cho dãy số (u_n), biết $u_n=\frac{n+1}{2n+1}.$ Số $\frac{8}{15}$ là số hạng thứ mấy của dãy số?

A. 8;                               

B. 6;                                

C. 5;                                

D. 7.

Hướng dẫn giải

Đáp án đúng là: D

Ta cần tìm n sao cho $u_n=\frac{n+1}{2n+1}=\frac{8}{15}\iff 15n+15=16n+8\iff n=7.$

Video bài giảng Toán 11 Bài 1: Dãy số – Chân trời sáng tạo

Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 5: Phương trình lượng giác cơ bản

Lý thuyết Bài 1: Dãy số

Lý thuyết Bài 2: Cấp số cộng

Lý thuyết Bài 3: Cấp số nhân

Lý thuyết Bài 1: Giới hạn của dãy số

Lý thuyết Bài 2: Giới hạn của hàm số

Xem thêm các bài tóm tắt lý thuyết chương Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Chương 1: Hàm số lượng giác và phương trình lượng giác

Lý thuyết Chương 2: Dãy số. Cấp số cộng. Cấp số nhân

Lý thuyết Chương 3: Giới hạn. Hàm số liên tục

Lý thuyết Chương 4: Đường thẳng và mặt phẳng. Quan hệ song song trong không gian

Lý thuyết Chương 5: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm