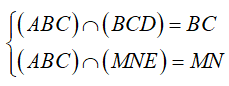BỘ 20 Đề thi Toán lớp 11 Học kì 1 năm 2022 – 2023 có đáp án

Đề thi Toán lớp 11 Học kì 1 năm 2022 – 2023 có đáp án (4 đề) – Đề 1

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 1 – Năm học ….

Môn: Toán lớp 11

Thời gian làm bài: 90 phút

(Đề 1)

Câu 1 : Cho  thỏa mãn  . Khi đó  có giá trị bằng:

Câu 2 : Gieo một đồng tiền cân đối và đồng chất bốn lần. Xác suất để cả bốn lần xuất hiện mặt sấp là?

Câu 3 : Cho hình bình hành ABCD. Phép tịnh tiến  biến:

A. B thành C

B. C thành A

C. C thành B

D. A thành D

Câu 4 : Một cuộc thi có 15 người tham dự, giả thiết rằng không có hai người nào có điểm bằng nhau. Nếu kết quả cuộc thi và việc chọn ra 4 người có điểm cao nhất thì có bao nhiêu kết quả có thể xảy ra?

A. 1635

B. 1536

C. 1356

D. 1365

Câu 5 : Tính chất nào sau đây không phải là tính chất của phép dời hình?

A. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng bảo toàn thứ tự của ba điểm đó.

B. Biến đường tròn thành đường tròn bằng nó.

C. Biến tam giác thành tam giác bằng nó, biến tia thành tia.

D. Biến đoạn thẳng thành đoạn thẳng có độ dài gấp k lần đoạn thẳng ban đầu k ≠ 1 .

Câu 6 : Giả sử bạn muốn mua một áo sơ mi cỡ 39 hoặc cỡ 40. Áo cỡ 39 có 5 màu khác nhau, áo cỡ 40 có 4 màu khác nhau. Hỏi có bao nhiêu sự lựa chọn (về màu áo và cỡ áo)?

A. 9

B. 5

C. 4

D. 10

Câu 7 : Cho  và điểm M'(4;2) . Biết là ảnh của M qua phép tịnh tiến  . Tìm M.

A. M(5;-3)

B. M(-3;5)

C. M(3;7)

D. M(-4;10)

Câu 8 : Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2sin²x – cos2x lần lượt là:

A. 2; −1

B. 3; −1

C. −1; −3

D. 3; 1

Câu 9 : Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x + 3y – 3 = 0 . Ảnh của đường thẳng d qua phép vị tự tâm O tỉ số k = 2 biến đường thẳng d thành đường thẳng có phương trình là:

A. 2x + 3y – 6 = 0

B. 4x + 2y – 5 = 0

C. 2x + 3y + 3 = 0

D. 4x – 2y – 3 = 0

Câu 10 : Cho hai đường thẳng song song a và b Trên a lấy 17 điểm phân biệt, trên b lấy 20 điểm phân biệt. Tính số tam giác mà có các đỉnh được chọn từ 37 điểm này.

A. 5690

B. 5960

C. 5950

D. 5420

Câu 11 : Có bao nhiêu phép quay tâm O góc α, 0 ≤ α ≤ 2π , biến tam giác đều có tâm O thành chính nó

A. 4

B. 1

C. 2

D. 3

Câu 12 : Điều kiện xác định của hàm số  là:

Câu 13 : Trong mặt phẳng Oxy cho đường tròn (C) có phương trình (x – 1)² + (y – 2)² = 4. Hỏi phép vị tự tâm O tỉ số k = -2 biến (C) thành đường tròn nào sau đây:

A. (x – 4)² + (y – 2)² = 4

B. (x – 4)² + (y – 2)² = 16

C. (x + 2)² + (y + 4)² = 16

D. (x – 2)² + (y – 4)² = 16

Câu 14 : Cho  và đường tròn  . Ảnh của (C) qua  là (C’) :

Câu 15 : Chu kỳ của hàm số  là:

Câu 16 : Có 5 tem thư khác nhau và 6 bì thư khác nhau. Từ đó người ta muốn chọn ra 3 tem thư, 3 bì thư và dán 3 tem thư ấy lên 3 bì đã chọn. Hỏi có bao nhiêu cách làm như thế?

A. 1000

B. 1200

C. 2000

D. 2200

Câu 17 : Ảnh của đường thẳng d: -3x + 4y + 5 = 0 qua phép đối xứng trục Ox là đường thẳng nào sau đây

A. 3x + 4y – 5 = 0

B. 3x – 4y – 5 = 0

C. -3x + 4y – 5 = 0

D. x + 3y – 5 = 0

Câu 18 : Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng.

Câu 19 : Ảnh của điểm P(-1;3) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O(0;0) góc quay 180^o và phép vị tự tâm O(0;0) tỉ số 2 là.

A. (2; -6)

B. (-2; 6)

C. (6; 2)

D. (- 6; -2)

Câu 20 : Cho  . Tính giá trị  .

Câu 21 : Trong một hộp chứa sáu quả cầu trắng được đánh số từ 1 đến 6 và ba quả cầu đen được đánh số 7; 8; 9 Có bao nhiêu cách chọn một trong các quả cầu ấy?

A.27

B. 9

C. 6

D. 3

Câu 22 : Tìm m để phương trình 5cosx – msinx = m + 1 có nghiệm

A. m ≤ 24

B. m ≥ 24

C. m ≤ 12

D. m ≤ -13

Câu 23 : Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Số cách sắp xếp sao cho bạn Chi luôn ngồi chính giữa là

A. 24

B. 120

C. 60

D. 16

Câu 24 : Phương trình:  tương đương với phương trình nào sau đây:

Câu 25 : Một thùng trong đó có 12 hộp đựng bút màu đỏ, 18hộp đựng bút màu xanh. Số cách khác nhau để chọn được đồng thời một hộp màu đỏ, một hộp màu xanh là?

A. 13

B. 12

C. 18

D. 216

Câu 26 : Phương trình 1 + cosx = m có đúng 2 nghiệm  khi và chỉ khi:

Câu 27 : Tìm hệ số của x¹² trong khai triển (2x – x²)¹⁰

Câu 28 : Giải phương trình 

Câu 29 : Số 253125000 có bao nhiêu ước số tự nhiên?

A. 160

B.240

C.180

D. 120

Câu 30 : Phương trình sinx = cosx chỉ có các nghiệm là:

Câu 31 : Tìm hệ số của x⁵ trong khai triển P(x) = x(1 – 2x)⁵ + x²(1 + 3x)¹⁰

A. 80

B. 3240

C. 3320

D. 259200

Câu 32 : Trong một ban chấp hành đoàn gồm 7 người, cần chọn ra 3 người vào ban thường vụ. Nếu cần chọn ban thường vụ gồm ba chức vụ Bí thư, Phó bí thư, Ủy viên thường vụ thì có bao nhiêu cách chọn?

A. 210

B. 200

C. 180

D. 150

Câu 33 : Phương trình  :

Câu 34 : Từ các chữ số 0; 1; 2;3 ; 4; 5 có thể lập được bao nhiêu số chẵn gồm 4 chữ số khác nhau

A. 156

B. 144

C. 96

D. 134

Câu 35 : Nghiệm của phương trình  là:

Câu 36 : Có bao nhiêu số tự nhiên gồm 7 chữ số khác nhau đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3?

A. 249

B. 7440

C. 3204

D. 2942

Câu 37 : Tính tổng  .

A. S = 3ⁿ

B. S = 2ⁿ

C. S = 3.2ⁿ

D. S = 4ⁿ

Câu 38 : Một hộp chứa 3 viên bi xanh, 5 viên bi đỏ và 6 viên bi vàng. Lấy ngẫu nhiên 6 viên bi từ hộp, tính xác suất để 6 viên bi được lấy ra có đủ cả ba màu.

Câu 39 : Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hai đường thằng có một điểm chung thì chúng có vô số điểm chung khác.

B. Hai đường thẳng song song khi và chỉ khi chúng không điểm chung.

C. Hai đường thẳng song song khi và chỉ khi chúng không đồng phẳng.

D. Hai đường thẳng chéo nhau khi và chỉ khi chúng không đồng phẳng.

Câu 40 : Cho tứ diện ABCD. Gọi I; J lần lượt là trọng tâm các tam giác ABD và ABC. Chọn khẳng định đúng trong các khẳng định sau?

A. IJ song song với CD

B. IJ song song với AB

C. IJ chéo CD

D. IJ cắt AB

Đáp án và Hướng dẫn làm bài

Câu 1 : Chọn D

Ta có 

Ta có 

Câu 2 : Chọn C

Số phần tử của không gian mẫu là 

Gọi A là biến cố Cả bốn lần gieo xuất hiện mặt sấp n(A) = 1

Vậy xác suất cần tính  .

Câu 3 : Chọn C

Vì ABCD là hình bình hành nên: 

Phép tịnh tiến  biến C thành B

Câu 4 : Chọn D

Nếu kết quả cuộc thi là việc chọn ra 4 người có điểm cao nhất thì mỗi kết quả ứng với một tổ hợp chập 4 của 15 phần tử.

Như vậy, ta có  kết quả.

Câu 5 : Chọn D

Tính chất D sai vì hai đoạn thẳng đó bằng nhau

Câu 6 : Chọn A

Nếu chọn cỡ áo 39 thì sẽ có 5 cách.

Nếu chọn cỡ áo 40 thì sẽ có 4 cách.

Theo qui tắc cộng, ta có 5 + 4 = 9 cách chọn mua áo.

Câu 7 : Chọn A

Ta có: 

Vậy M (5; -3)

Câu 8 : Chọn B

Câu 9 : Chọn A

Câu 10 : Chọn C

Một tam giác được tạo bởi ba điểm phân biệt nên ta xét:

TH1. Chọn 1 điểm thuộc a và 2 điểm thuộc b có  tam giác.

TH2. Chọn 2 điểm thuộc a và 1 điểm thuộc b có  tam giác.

Như vậy, ta có  tam giác cần tìm.

Câu 11 : Chọn A

Các phép quay thỏa mãn bài toán là 

Câu 12 : Chọn D

Điều kiện: 

Câu 13 : Chọn C

Đường tròn (C ) có tâm 

Phép vị tự tâm O, tỉ số k = -2; biến tâm I thành tâm I’ nên:

Câu 14 : Chọn B

Đường tròn (C ) có tâm I(1; -2) và R = 3.

Tinh tiến theo  biến tâm I thành tâm I’ nên:

Đường tròn (C’) có tâm I’ ( 4; 1) và bán kính R’ = R = 3 có phương trình:

(x – 4)⁴ + (y + 1)² = 4

Câu 15 : Chọn A

Hàm số y = tanx(ax + b) (a ≠ 0) có chu kỳ 

Câu 16 : Chọn B

Số cách chọn 3 tem thư trong 5 tem thư khác nhau là:  cách.

Số cách chọn 3 bì thư trong 6 bì thư khác nhau là:  cách.

Số cách dán tem thư thứ nhất vào 3 bì thư là:  cách.

Số cách dán tem thư thứ hai vào 2 bì thư còn lại là:  cách.

Số cách dán tem thư thứ hai vào bì thư cuối cùng là:  cách.

Vậy có  cách làm thỏa mãn yêu cầu bài toán.

Câu 17 : Chọn A

Đường thẳng d cắt trục Ox tại điểm có hoành độ  và trục tung tại điểm có tung độ 

Đường thẳng d’ là ảnh của đường thẳng d qua phép đối xứng trục Ox cắt trục Ox tại điểm có hoành độ  và trục tung tại điểm có tung độ 

Phương trình đoạn chắn của 

Câu 18 : Chọn B

Không gian mẫu là số cách chọn ngẫu nhiên 5 viên bi từ hộp chứa 18 viên bi. Suy ra số phần tử của không gian mẫu là  .

Gọi A là biến cố 5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng . Ta có các trường hợp thuận lợi cho biến cố A là :

● TH1: Chọn 1 bi đỏ, 1 bi vàng và 3 bi xanh nên có  cách.

● TH2: Chọn 2 bi đỏ, 2 bi vàng và 1 bi xanh nên có  cách.

Suy ra số phần tử của biến cố A là  .

Vậy xác suất cần tính  .

Câu 19 : Chọn A

Gọi M(x;y) là ảnh của P qua phép quay tâm O, góc quay 180°.

Khi đó O là trung điểm của MP suy ra M(1;-3) .

Phép vị tự tâm O, tỉ số k = 2 biến điểm M thành điểm N nên:

Câu 20 : Chọn D

Ta có : 

Câu 21 : Chọn B

Vì các quả cầu trắng hoặc đen đều được đánh số phân biệt nên mỗi lần lấy ra một quả cầu bất kì là một lần chọn.

Nếu chọn một quả trắng có 6 cách.

Nếu chọn một quả đen có 3 cách.

Theo qui tắc cộng, ta có 6 + 3= 9 cách chọn.

Câu 22 : Chọn C

Để phương trình đã cho có nghiệm khi:

Câu 23 : Chọn A

Xếp bạn Chi ngồi giữa có 1 cách.

Số cách xếp 4 bạn sinh An, Bình, Dũng, Lệ vào 4 chỗ còn lại là một hoán vị của 4 phần tử nên có có 4! = 24 cách.

Vậy có 24 cách xếp.

Câu 24 : Chọn C

Ta có : 

Câu 25 : Chọn D

Để chọn một hộp màu đỏ và một hộp màu xanh, ta có:

Có 12 cách chọn hộp màu đỏ.

Có 18 cách chọn hộp màu xanh.

Vậy theo qui tắc nhân ta có 12. 18 = 216 cách.

Câu 26 : Chọn A

Phương trình đã cho có 2 nghiệm  khi và chỉ khi

Câu 27 : Chọn B

Theo khai triển nhị thức Niu-tơn, ta có

Số hạng đứng thứ k + 1 là:

Hệ số của x¹² ứng với 10 + k = 12 nên k = 2

Hệ số cần tìm 

Câu 28 : Chọn C

Đặt 

Do đó sin2x = 1 – t² .

Câu 29 : Chọn C

Ta có: 253125000= 23. 34. 58 nên mỗi ước số tự nhiên của số đã cho đều có dạng 2^m x 3ⁿ x 5^p trong đó m,n,p ∈ N sao cho 0 ≤ m ≤ 3 ; 0 ≤ n ≤ 4; 0 ≤ p ≤ 8

Có 4 cách chọn m

Có 5 cách chọn n

Có 9 cách chọn p

Vậy theo qui tắc nhân ta có 4.5.9 = 180 ước số tự nhiên.

Câu 30 : Chọn A

Ta có : 

Câu 31 : Chọn C

Theo khai triển nhị thức Niu-tơn, ta có

số hạng chứa x⁵ tương ứng với 6- k = 5 nên k = 1 .

Tương tự, ta có  .

số hạng chứa x⁵ tương ứng với 12 – l= 5 hay l = 7.

Vậy hệ số của x⁵ cần tìm là  .

Câu 32 : Chọn A

Số cách chọn ban thường vụ gồm ba chức vụ Bí thư, Phó bí thư, Ủy viên thường vụ từ 7 người là số các chỉnh hợp chập ba của bảy phần tử

Câu 33 : Chọn D

Câu 34 : Chọn A

Gọi số cần tìm có dạng  với a,b,c,d ∈ A = {0,1,2,3,4,5}

Vì  là số chẵn ⇒ d = {0,2,4}

TH1. Nếu d = 0 số cần tìm là  Khi đó:

a được chọn từ tập A\{0} nên có 5 cách chọn.

b được chọn từ tập A\{0,a} nên có 4 cách chọn.

c được chọn từ tập A\{0,a,b} nên có 3 cách chọn.

Như vậy, ta có 5.4.3 = 60 số có dạng 

TH2. Nếu d = {2,4} ⇒ d có 2 cách chọn.

Khi đó a: có 4 cách chọn (khác 0 và d),

b: có 4 cách chọn và c có 3 cách chọn.

Như vậy, ta có 2.4.4.3 = 96 số cần tìm như trên.

Vậy có tất cả 60 +96 = 156 số cần tìm.

Câu 35 : Chọn B

Điều kiện: sin2x ≠ 0 .

Phương trình tương đương 

Câu 36 : Chọn B

Ta chia thành các trường hợp sau:

TH1: Nếu số 123 đứng đầu thì có  số.

TH2: Nếu số 321 đứng đầu thì có  số.

TH3: Nếu số 123; 321 không đứng đầu

Khi đó có 6 cách chọn số đứng đầu ( khác 0; 1; 2; 3 ),

khi đó còn 6 vị trí có 4 cách xếp 3 số 321 hoặc 123, còn lại 3 vị trí có  cách chọn các số còn lại. Do đó trường hợp này có 6.2.4. = 5760

Suy ra tổng các số thoả mãn yêu cầu là 2. + 5760 = 7440 .

Câu 37 :

Khai triển nhị thức Niu-tơn của (1 + x)ⁿ , ta có

Cho x = 3, ta được:

Câu 38 : Chọn A

Không gian mẫu là số cách chọn ngẫu nhiên 6 viên bi từ hộp chứa 14 viên bi. Suy ra số phần tử của không gian mẫu là  .

Gọi A là biến cố 6 viên bi được lấy ra có đủ cả ba màu .

Để tìm số phần tử của biến cố A ta đi tìm số phần tử của biến cố  tức là 6 viên bi lấy ra không có đủ ba màu như sau:

● TH1: Chọn 6 viên bi chỉ có một màu (chỉ chọn được màu vàng).

Do đó trường hợp này có  cách.

● TH2: Chọn 6 viên bi có đúng hai màu xanh và đỏ, có  cách.

Chọn 6 viên bi có đúng hai màu đỏ và vàng, có  cách.

Chọn 6 viên bi có đúng hai màu xanh và vàng, có  cách.

Do đó trường hợp này có  cách.

Suy ra số phần tử của biến cố  là .

Suy ra số phần tử của biến cố  là .

Vậy xác suất cần tính 

Câu 39 : Chọn D

A sai. Trong trường hợp 2 đường thẳng cắt nhau thì chúng chỉ có 1 điểm chung.

B và C sai. Hai đường thẳng song song khi và chỉ khi chúng đồng phằng và không có điểm chung.

Câu 40 : Chọn A

Gọi M;N lần lượt là trung điểm của BD; BC

là đường trung bình của tam giác BCD ⇒ MN // CD

Vì I; J lần lượt là trọng tâm các tam giác ABD và ABC ⇒ 

Từ (1) và (2) suy ra: IJ // CD

Đề thi Toán lớp 11 Học kì 1 năm 2022 – 2023 có đáp án (4 đề) – Đề 2

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 1 – Năm học ….

Môn: Toán lớp 11

Thời gian làm bài: 90 phút

(Đề 2)

I. TRẮC NGHIỆM (5 điểm)

Câu 1 : Giá trị lớn nhất, nhỏ nhất của hàm số y= 3 – 2cos²x lần lượt là:

A. y_max = 3, y_min = 1

B. y_max = 1, y_min = -1

C. y_max = 5, y_min = 1

D. y_max = 5, y_min = -1

Câu 2 : Trong 1 tổ có 6 học sinh nam và 4 học sinh nữ. Chọn ngẫu nhiên 3 bạn trong tổ tham gia đội tình nguyện của trường. Tính xác suất để 3 bạn được chọn toàn nam?

Câu 3 : Cho hình chóp S.ABCD có đáy là hình thang ABCD ( AD// BC). Gọi M là trung điểm của CD. Giao tuyến của hai mặt phẳng (SBM) và (SAC) là:

A. SP (P là giao điểm của AB và CD).

B. SO (O là giao điểm của AC và BD)

C. SJ (J là giao điểm của AM và BD)

D. SI (I là giao điểm của AC và BM)

Câu 4 : Trong mặt phẳng tọa độ Oxy, tìm ảnh của đường tròn (c):(x-1)² + (y + 2)² = 4 qua phép đối xứng trục Ox.

A. (C’):(x + 1)² + (y + 2)² = 4

B. (C’):(x + 1)² + (y – 2)² = 4

C. (C’):(x – 1)² + (y – 2)² = 4

D. (C’):(x – 1)² + (y – 2)² = 2

Câu 5 : Nghiệm của phương trình 2sin x + 1 = 0 là:

Câu 6 : Dãy số (u_n) có  là dãy số:

A. Giảm

B. Không tăng, không giảm

C. Tăng

D. Không bị chặn

Câu 7 : Tìm số hạng thứ 11 của cấp số cộng có số hạng đầu bằng 3 và công sai d = -2.

A. – 21

B. 23

C. – 17

D.- 19

Câu 8 : Trong mặt phẳng tọa độ ( Oxy), ảnh của điểm M(1; -2) qua phép vị tự tâm O tỉ số k = -2 là:

Câu 9 : Trong mặt phẳng, cho 6 điểm phân biệt sao cho không ba điểm nào thẳng hàng. Hỏi có thể lập được bao nhiêu tam giác mà các đỉnh của nó thuộc tập điểm đã cho?

Câu 10 : Tìm tập xác định của hàm số y = tan x

Câu 11 : Trong các mệnh đề sau, mệnh đề nào sai ?

A. “Phép vị tự tỉ số k = -1 là phép dời hình”.

B. “Phép đối xứng tâm biến đường tròn thành đường tròn có cùng bán kính”

C. “Phép đối xứng trục biến đường thẳng thành đường thẳng song song với nó”

D. “Phép quay tâm I góc quay 90° biến đường thẳng thành đường thẳng vuông góc với nó.”

Câu 12 : Tìm số hạng chứa x³ trong khai triển 

Câu 13 : Nghiệm của phương trình sinx – cos2x = 2 là:

Câu 14 : Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, AC. E là điểm trên cạnh CD với ED = 3EC. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là:

A. Tam giác MNE

B. Hình thang MNEF với F là điểm trên cạnh BD mà EF// BC

C. Tứ giác MNEF với F là điểm bất kì trên cạnh BD

D. Hình bình hành MNEF với F là điểm trên cạnh BD mà EF// BC

Câu 15 : Trong mặt phẳng tọa độ Oxy, tìm ảnh của đường thẳng  qua phép tịnh tiến theo 

Câu 16 : Có bao nhiêu số tự nhiên có 5 chữ số được thành lập từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9.

Câu 17 : Một hình chóp có tổng số đỉnh và số cạnh bằng 13. Tìm số cạnh của đa giác đáy.

A. 4

B. 3

C. 5

D. 6

Câu 18 : Tìm mệnh đề đúng trong các mệnh đề sau

A. Nếu hai mặt phẳng  và  song song với nhau thì mọi đường thẳng nằm trong  đều song song với mọi đường thẳng nằm trong  B. Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân biệt  và  thì  và  song song với nhau C. Qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó D. Nếu hai mặt phẳng  và  song song với nhau thì mọi đường thẳng nằm trong  đều song song với 

Câu 19 : Tìm công bội q của một cấp số nhân  có và 

Câu 20 : Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm I, J lần lượt là trọng tâm tam giác SAB, SAD. M là trung điểm CD. Chọn mệnh đề đúng trong các mệnh đề sau:

A. IJ // (SCD)

B. IJ // (SBD)

C. IJ // (SBC)

D. IJ // (SBM)

II. TỰ LUẬN (5 điểm)

Câu 1 (1 điểm) : Giải phương trình sau: 

Câu 2 (1 điểm) : Đội thanh niên xung kích của một trường phổ thông có 10 học sinh, gồm 4 học sinh lớp A, 3 học sinh lớp B và 3 học sinh lớp C. Hỏi có bao nhiêu cách chọn 5 học sinh đi làm nhiệm vụ mà số học sinh lớp B bằng số học sinh lớp C

Câu 3 (1 điểm) : Tìm số hạng không chứa x trong khai triển 

Câu 4 (2 điểm) : Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi N là trung điểm của cạnh SC. Lấy điểm M đối xứng với B qua A.

a) Chứng minh rằng: MD song song với mặt phẳng (SAC).

b) Xác định giao điểm G của đường thẳng MN với mặt phẳng (SAD). Tính tỉ số  .

Đáp án và Hướng dẫn làm bài

Câu 1 : Chọn A

Ta có:

Câu 2 : Chọn D

Số phần tử của không gian mẫu: 

Gọi A: “3 bạn được chọn toàn nam”.

Khi đó,  .

Câu 3 : Chọn D

Trong (ABCD), gọi I là giao điểm của AC và BM

Khi đó: 

Mà  .

Câu 4 : Chọn C

+ Đường tròn (C ): ( x- 1)² + (y + 2)² = 4 có tâm I( 1; -2), bán kính R = 2

+ Qua phép đối xứng trục Ox, biến tâm I (1; -2) thành tâm I’ (1; 2); bán kính R’ = R= 2.

Do đó. ảnh của đường tròn (C )qua phép đối xứng trục Ox là:

(C’):(x-1)² + (y-2)² = 4

Câu 5 : Chọn A

Câu 6 : Chọn C

Ta có: u_n > 0 với n > 0.  Do đó, dãy số đã cho là dãy tăng.

Câu 7 : Chọn C

Theo đề bài, ta có: 

Câu 8 : Chọn D

Câu 9 : Chọn D

Từ 6 điểm phân biệt sao cho không ba điểm nào thẳng hàng có thể lập được số tam giác là:  .

Câu 10 : Chọn C

Tập xác định của hàm số y = tan x là: 

Câu 11 : Chọn C

“Phép đối xứng trục biến đường thẳng thành đường thẳng song song với nó” là mệnh đề sai. Vì hai đường thẳng có thể trùng nhau ( nếu tâm đối xứng nằm trên đường thẳng d).

Câu 12 : Chọn D

Ta có:

Số hạng chứa x³ trong khai triển ứng với i thỏa mãn: 2i – 9 = 3 ⇔ i = 6

⇒ Số hạng chứa x³ trong khai triển là:

 .

Câu 13 : Chọn C

Câu 14 : Chọn B

Định lý về giao tuyến của ba mặt phẳng: Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng qui hoặc đôi một song song với nhau.

Xét ba mặt phẳng phân biệt (ABC), (BCD), (MNE) có:

Mà MN // BC ⇒ EF // BC (F là giao điểm của MNE với đường thẳng BD)

Từ E, ta kẻ EF // BC, F ∈ BC

⇒ MNEF là hình thang

(Do  không phải hình bình hành)

Câu 15 : Chọn A

Phép tịnh tiến theo 

Suy ra; d’ song song hoặc trùng với d.

Đường thẳng d’ có dạng: x + 2y + m = 0

Lấy  . Phép tịnh tiến  với 

Vì  nên  .

Câu 16 : Chọn D

Giả sử số đó là  . Khi đó:

Các số  đều có 9 cách chọn, 

Lập được tất cả 9⁵ số.

Câu 17 : Chọn A

Giả sử hình chóp có n cạnh bên. Khi đó, số đỉnh là n + 1 , số cạnh là 2n.

Theo đề bài, ta có: n + 1 +2n = 13 ⇔ 3n = 12 ⇔ n = 4

Số cạnh của đa giác đáy là 4.

Câu 18 : Chọn D

Nếu hai mặt phẳng  và  song song với nhau thì mọi đường thẳng nằm trong  đều song song với  : là mệnh đề đúng.

Câu 19 : Chọn A

 và 

Câu 20 : Chọn B

Gọi E, F lần lượt là trung điểm của AB, AD.

Do I, J lần lượt là trọng tâm tam giác SAB, SAD nên:

Mà EF // BD (vì EF là đường trung bình của ΔABD ) .

⇒ IJ // BD ⇒ IJ // (SBD)

II. TỰ LUẬN (5 điểm)

Câu 1 :

Đặt 

Phương trình đã cho trở thành

Câu 2 :

Số cách chọn 5 học sinh, trong đó: 1 học sinh lớp A, 2 học sinh lớp B, 2 học sinh lớp C là:  (cách)

Số cách chọn 5 học sinh, trong đó: 3 học sinh lớp A, 1 học sinh lớp B, 1 học sinh lớp C là:  (cách)

Vậy có tất cả số cách chọn 5 học sinh đi làm nhiệm vụ mà số học sinh lớp B bằng số học sinh lớp C là: 36 + 36 = 72 (cách).

Câu 3 :

Ta có:

Số hạng không chứa x trong khai triển ứng với i thỏa mãn: 5i- 15 ⇔ i = 3

⇒ Số hạng không chứa x trong khai triển là:  .

Câu 4 :

a) Chứng minh rằng: MD song song với mặt phẳng (SAC).

Do ABCD là hình bình hành nên  , mà M đối xứng với B qua A

 là hình bình hành ⇒ MD // AC

Vì AC ⊂ (SAC) ⇒ MD // (SAC)

b) Xác định giao điểm G của đường thẳng MN với mặt phẳng (SAD). Tính tỉ số 

Gọi E là giao điểm của AD và MC.

Do ACDM là hình bình hành nên E là trung điểm của MC

Trong (SMC) gọi G là giao điểm của SE và MN ⇒ 

Mà 

Tam giác SMC có: SE, MN là trung tuyến, SE ∩ MN = G ⇒ G là trọng tâm tam giác SMC ⇒ 

 

Đề thi Toán lớp 11 Học kì 1 năm 2022 – 2023 có đáp án (4 đề) – Đề 3

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 1 – Năm học ….

Môn: Toán lớp 11

Thời gian làm bài: 90 phút

(Đề 3)

Câu 1 : Phương trình:  có các nghiệm là

Câu 2 : Số nghiệm của phương trình  trong khoảng  là

A. 5

B. 7

C. 4

D. 6

Câu 3 : Phương trình  tương đương với phương trình

Câu 4 : Cho đa giác đều n đỉnh,  . Tìm n biết rằng đa giác đã cho có 135 đường chéo.

A. n = 15

B. n = 27

C. n = 8

D. n = 18

Câu 5 : Phương trình nào sau đây vô nghiệm

Câu 6 : Cho đường tròn  . Ảnh của đường tròn (C) qua phép Đ_O là đường tròn có phương trình nào dưới đây?

Câu 7 : Gieo một con xúc sắc cân đối đồng chất hai lần. Tính xác suất sao cho tổng số chấm của hai lần gieo là số lẻ

Câu 8 : Tập nghiệm của phương trình 

Câu 9 : Điều kiện xác định của hàm số  là

Câu 10 : Trong các khẳng định sau, khẳng định nào sai

Câu 11 : Tập xác định của hàm số  là

Câu 12 : Giải phương trình 

Câu 13 : Lớp 11A7 có 18 nam và 24 nữ. Chọn ngẫu nhiên hai học sinh để hát song ca. Xác suất để trong đó có ít nhất một nam là?

Câu 14 : Giá trị nhỏ nhất của y = 4 – 3cos2x là

A. 1

B. 7

C. -7

D. -3

Câu 15 : Cho tập A = {0;1;2;3;4;5;6;7} .Từ tập A có thể lập được bao nhiêu số tự nhiên chẵn có bốn chữ số đôi một khác nhau?

A. 2048

B. 420

C. 840

D. 750

Câu 16 : Cho đường thẳng  . Điểm nào sau đây thuộc đường thẳng (d) :

A. (-1;5)

B. (-2;3)

C. (2;3)

D. (-3;-1)

Câu 17 : Một tổ gồm 7 nam và 6 nữ. Hỏi có bao nhiêu cách chọn 4 em đi trực nhật sao cho có ít nhất 2 nữ?

Câu 18 : Phương trình 2cosx + 1 = 0 có nghiệm là

Câu 19 : Trong các mệnh đề sau, mệnh đề nào đúng?

A. Phép đối xứng trục là phép đồng nhất

B. Thực hiện liên tiếp phép quay và phép vị tự ta được phép đồng dạng.

C. Phép đồng dạng là một phép dời hình.

D. Phép vị tự là một phép dời hình.

Câu 20 : Cho 2 đường thẳng song song. Trên đường thẳng thứ nhất lấy 7 điểm phân biệt, trên đường thẳng thứ hai lấy 9 điểm phân biệt. Hỏi có bao nhiêu tam giác có các đỉnh thuộc tập 16 điểm đã lấy trên hai đường thẳng trên?

A. 560 tam giác.

B. 270 tam giác.

C. 441 tam giác.

D. 150 tam giác.

Câu 21 : Từ một hộp chứa ba quả cầu trắng và hai quả cầu đen, lấy ngẫu nhiên đồng thời hai quả. Tính xác suất để hai quả đó cùng màu

Câu 22 : Giá trị nhỏ nhất của hàm số y = 2sinx – cosx là

Câu 23 : Gieo một đồng xu cân đối và đồng chất liên tiếp ba lần. Gọi A là biến cố “Có ít nhất hai mặt sấp xuất hiện liên tiếp” và B là biến cố “Kết quả ba lần gieo là như nhau”. Xác định biến cố A ∪ B

Câu 24 : Trong mp oxy cho  và điểm A(1;3) . Tìm ảnh của A qua phép  ?

A. (-1;2)

B. (-1;-2)

C. (1;-2)

D. (3;4)

Câu 25 : Có hai chiếc hộp: Hộp thứ nhất chứa bốn bi xanh, ba bi vàng; Hộp thứ hai chứa hai bi xanh, một bi đỏ. Lấy ngẫu nhiên từ mỗi hộp một viên bi. Xác suất để được hai bi xanh là;

Câu 26 : Biết n là số nguyên dương thỏa mãn  . Giá trị của n là:

A. 15

B. 16

C. 14

D. 12

Câu 27 : Trong mặt phẳng, với hệ tọa độ Oxy , cho điểm M(1;-3) . Phép tịnh tiến theo véctơ  biến M thành điểm

A. M'(1;7)

B. M'(3;2)

C. M'(3;1)

D. M'(-1;-7)

Câu 28 : Trong mp Oxy cho đường thẳng d có phương trình 3x + y – 3 = 0 . Ảnh của đường thẳng d qua phép V_(O;-2) biến đường thẳng d thành đường thẳng có phương trình là:

A. -3x + y + 3 = 0

B. 3x + y + 6 = 0

C. 3x + y – 6 = 0

D. 3x + y – 3 = 0

Câu 29 : Lớp 11A7 có 18 học sinh nam và 24 học sinh nữ. Thầy chủ nhiệm cần chọn 10 học sinh để luyện tập vũ khúc sân trường. Hỏi thầy chủ nhiệm có bao nhiêu cách chọn 10 học sinh sao cho có ít nhất 1 học sinh nữ?

Câu 30 : Hàm số y = sin2x – tan2x tuần hoàn với chu kỳ là bao nhiêu?

Câu 31 : Giải phương trình 

Câu 32 : Sắp xếp 5 người trong đó có An và Linh ngồi vào 5 ghế thẳng hàng. Xác suất để An và Linh không ngồi cạnh nhau là:

Câu 33 : Từ thành phố A tới thành phố B có 4 con đường, từ thành phố B tới thành phố C có 5 con đường. Hỏi có bao nhiêu cách đi từ A tới C qua B chỉ một lần.

A.9

B. 20

C. 1

D. 25

Câu 34 : Phương trình sin²x – 3sinx + 2 = 0

Câu 35 : Trong mặt phẳng mo Oxy cho đường thẳng d có phương trình: x – 2y + 3 = 0 . Ảnh của đường thẳng d qua phép tịnh tiến theo véctơ  có phương trình:

A. x – 2y + 1 = 0

B. x – 2y + 3 = 0

C. 2x – 4y + 3 = 0

D. x – 2y – 1 = 0

Câu 36 : Phép vị tự tâm O(0;0) tỉ số -2 biến đường tròn : (x – 1)² – (y – 2)² = 4 thành:

A. (x – 2)² – (y – 4)² = 16

B. (x – 4)² – (y – 2)² = 4

C. (x – 1)² – (y – 2)² = 16

D. (x + 2)² + (y + 4)² = 16

Câu 37 : Phương trình 

Câu 38 : Để chào mừng ngày 26/3 Đoàn trường THPT XXX tổ chức giải bóng đá có 10 đội tham dự theo thể thức thi đấu vòng tròn tính điểm (hai đội bất kỳ đều gặp nhau đúng 1 trận). Hỏi đoàn trường phải tổ chức bao nhiêu trận đấu ?

A. 10 trận

B. 45 trận

C. 90 trận

D. Kết quả khác

Câu 39 : Đường thẳng đi qua điểm A(-2;1) và song song với đường thẳng y = 2x – 3 có phương trình là

A. y = -2x + 3

B. y = 2x – 6

C. y = 2x + 5

D. y = -2x – 5

Câu 40 : Cho tập A = {0;1;2;3;4;5;6;7;8;9} . Số các số tự nhiên có năm chữ số đôi một khác nhau được lấy ra từ tập A là

A. 30420

B. 27216

C. 15120

D. 27162

Câu 41 : Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x – 3y + 1 = 0 . Để phép tịnh tiến theo vector  biến đường thẳng d thành chính nó thì  phải là vecto nào trong số các vecto sau ?

Câu 42 : Một thùng có 7 sản phẩm, trong đó có 4 sản phầm loại I và 3 sản phầm loại II. Lấy ngẫu nhiên 2 sản phẩm. Xác suất để lấy được 2 sản phẩm cùng loại là

Câu 43 : Số hạng không chứa x trong khai triển  là

Câu 44 : Cho tanα = -2 . Giá trị của biểu thức 

Câu 45 : Phương trình  có các họ nghiệm là:

Câu 46 : Trong mặt phẳng tọa độ Oxy cho điểm M'(-3;2) là ảnh của điểm M qua phép quay tâm O góc 90^o thì điểm M có tọa độ là:

A. (2;-3)

B. (2;3)

C. (-2;-3)

D. (3;-2)

Câu 47 : Tính 

A. 2²⁰¹⁸ – 1

B. 2²⁰¹⁸ + 1

C. 2²⁰¹⁸

D. 2²⁰¹⁸ – 2

Câu 48 : Trong mặt phẳng Oxy cho đường thẳng d: x + 2y – 3 = 0 . Hỏi phép dời hình có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = 2 và phép tịnh tiến theo vector  biến d thành đường thẳng d’ có phương trình:

A. x + 2y – 6 = 0

B. x + 2y – 11 = 0

C. x + 2y + 6 = 0

D. x + 2y + 11 = 0

Câu 49 : Tập xác định của hàm số  là:

Câu 50 : Trong các giá trị sau, giá trị nào là nghiệm của phương trình : 

Đáp án và Hướng dẫn làm bài

Câu 1 : Chọn B

Ta thấy cosx = 0 không thỏa mãn phương trình đã cho

chia cả 2 vế của phương trình cho cos²x , ta được:

Câu 2 : Chọn A

Câu 3 : Chọn A

Phương trình đã cho

Câu 4 : Chọn D

Đa giác lồi n đỉnh thì có n cạnh. Nếu vẽ tất cả các đoạn thẳng nối từng cặp trong n đỉnh này thì có một bộ gồm các cạnh và các đường chéo.

Vậy để tính số đường chéo thì lấy tổng số đoạn thẳng dựng được trừ đi số cạnh, với

• Tất cả đoạn thẳng dựng được là bằng cách lấy ra 2 điểm bất kỳ trong n điểm, tức là số đoạn thẳng chính là số tổ hợp chập 2 của n phần tử.

Như vậy, tổng số đoạn thẳng là 

• Số cạnh của đa giác lồi là n

Suy ra số đường chéo của đa giác đều n đỉnh là 

Theo bài ra, ta có 

Câu 5 : Chọn B

Các phương trình ở các đáp án A, C và D có nghiệm.

Xét phương trình: 2sinx – 3cosx = 4

Vì 4² < 2² + (-3)² nên phương trình vô nghiệm

Câu 6 : Chọn B

Đường tròn (C) có tâm I(-2;1) và bán kính R = 3

D₀(I) = I'(2;-1)

Gọi (C’) là ảnh của (C) qua phép D₀ ⇒ (C’) tâm I'(2′-1) và bán kính R’ = R = 3 .

Khi đó (C’): (x – 2)² + (y + 1)² = 9

Câu 7 : Chọn A

Số phần tử của không gian mẫu là: n(Ω)= 6.6 = 36 (phần tử)

Để tổng số chấm lẻ thì số cách chọn là: 6.3 = 18 (cách)

Xác suất để tổng số chấm của hai lần gieo là số lẻ là: 

Câu 8 : Chọn D

Điều kiện: 

Với điều kiện (*) phương trình đã cho

Câu 9 : Chọn C

Câu 10 : Chọn B

Câu 11 : Chọn B

Câu 12 : Chọn B

Câu 13 : Chọn B

Số cách chọn ngẫu nhiên 2 học sinh là:  (Cách)

Số cách chọn 2 học sinh để có ít nhất 1 nam là:  (Cách)

Xác suất để có ít nhất 1 nam là: 

Câu 14 : Chọn A

Câu 15 : Chọn D

Gọi số tự nhiên có 4 chữ số thỏa mãn đề bài là 

+) Nếu d = 0 thì số cách chọn abc là:  (cách)

+) Nếu d ∈ {2;4;6} thì a có 6 cách chọn ⇒ số cách chọn là bc là 

Trong trường hợp này có: 3.6. = 540 (cách)

Số các số thỏa mã đề bài là: 210 + 540 = 710 (số)

Câu 16 : Chọn A

Thay điểm x = -1 ⇒ t = 1 ⇒ y = 5 ⇒ điểm (1;-5) ∈ d

Câu 17 : Chọn B

Có các cách chọn sau:

+) 2 nữ, 2 nam  (cách)

+) 3 nữ, 1 nam  (cách)

+) 4 nữ  (cách)

Theo quy tắc cộng, số cách chọn là:  (cách)

Câu 18 : Chọn A

Phương trình đã cho 

Câu 19 : Chọn B

Câu 20 : Chọn C

TH1. Lấy 2 điểm thuộc d₁ ; 1 điểm thuộc d₂ có  tam giác

TH2. Lấy 1 điểm thuộc d₂ ; 2 điểm thuộc d₁ có  tam giác

Vậy số tam giác cần tìm là 

Câu 21 : Chọn D

Lấy ngẫu nhiên 2 quả cầu trong 5 quả cầu có  cách

TH1. 2 quả cầu lấy ra cùng màu trắng ⇒ có  cách

TH1. 2 quả cầu lấy ra cùng màu đen ⇒ có  cách

Vậy xác suất cần tính là 

Câu 22 : Chọn C

Câu 23 : Chọn C

Phần tử của biến cố B là B = {SSS;NNN}

Phần tử của biến cố A là A = {SSN;SSS;NSS} .

Vậy A ∪ B = {SSS;SSN;;NSS;NNN}

Câu 24 : Chọn D

Câu 25 : Chọn C

Lấy 1 bi từ hộp thứ nhất có 7 cách, 1 bi từ hộp thứ hai có 3 cách ⇒ n(Ω) = 3.7 = 21

Lấy 1 bi xanh từ hộp thứ nhất có 4 cách, 1 bi xanh từ hộp thứ hai có 2 cách ⇒ n(X) = 4.2 = 8

Vậy xác suất cần tính là 

Câu 26 : Chọn D

Câu 27 : Chọn C

Câu 28 : Chọn B

Câu 29 : Chọn B

Lớp học có tất cả 42 học sinh

Số cách chọn 10 học sinh từ 42 học sinh là 

Giả sử trong 10 học sinh được chọn không có học sinh nữ có  cách chọn

Vậy số cách chọn thỏa mãn yêu cầu bài toán là 

Câu 30 : Chọn D

Hàm số y = sin 2x tuần hoàn với chu kì 

Hàm số y = tan2x tuần hoàn với chu kì 

Do đó; hàm số đã cho tuần hoàn với chu kì T = π

Câu 31 : Chọn C

Câu 32 : Chọn D

Sắp xếp 5 người vào 5 ghế có 5! = 120 cách

Giả sử An và Linh ngồi cạnh nhau, khi đó coi An và Linh là một phần tử + 3 người còn lại ngồi vào ghế.

Khi đó, có 2!.4! = 48 cách sắp xếp để An và Linh ngồi cạnh nhau

Vậy có 120 – 48 = 72 cách sắp xếp để An và Linh không ngồi cạnh nhau

Câu 33 : Chọn B

Đi từ A → B có 4 cách, đi từ B → C có 5 cách.

Theo quy tắc nhân, đi từ A → C có 4 x 5 = 20 cách

Câu 34 : Chọn A

Câu 35 : Chọn D

Câu 36 : Chọn D

Câu 37 : Chọn A

Câu 38 : Chọn B

Cứ 2 đội ta sẽ có 1 trận bóng đá

Với 10 đội, đoàn trưởng phải tổ chức số trận là 

Câu 39 : Chọn C

Gọi phương trình đường thẳng cần tìm là (d): y = ax + b

Vì

Mà (d) đi qua A(2;-1) ⇒ -2a + b = 1 ⇔ b = 5

Vậy phương trình đường thẳng d): y = 2x + 5

Câu 40 : Chọn B

Gọi số cần tìm có dạng  với a,b,c,d,e ∈ A

Suy ra a có 9 cách chọn, b có 9 cách chọn, c có 8 cách chọn, d có 7 cách chọn, e có 6 cách chọn.

Khi đó, có tất cả 9.9.8.7.6 = 27216 số cần tìm

Câu 41 : Chọn A

Giả sử vector  .

Gọi M(x;y) là điểm thuộc đường thẳng d và M'(x’;y’) là ảnh của đường thẳng d qua phép tịnh tiến vector  .

Câu 42 : Chọn B

Câu 43 : Chọn C

Ta có : 

Số hạng không chứa x khi 12 – 4k = 0 ⇔ k =3 ⇒ số hạng đó là 

Câu 44 : Chọn D

Ta có 

Câu 45 : Chọn D

Câu 46 : Chọn B

Điểm M(-3;2) là ảnh của điểm M(2;3) qua phép quay tâm O góc 90^o

Câu 47 : Chọn D

Câu 48 : Chọn B

Gọi M(x;y) là điểm thuộc đường thẳng d, M'(x’;y’) là điểm thuộc đường thẳng d₁ là ảnh của d qua phép vị tự tâm O tỉ số k = 2, M”(x”;y”) là điểm thuộc đường thẳng d” là ảnh của d₁ qua phép tịnh tiến theo vector 

Câu 49 : Chọn D

Điều kiện: 

Câu 50 : Chọn C

Đề thi Toán lớp 11 Học kì 1 năm 2022 – 2023 có đáp án (4 đề) – Đề 4

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 1 – Năm học ….

Môn: Toán lớp 11

Thời gian làm bài: 90 phút

(Đề 4)

 

Câu 1 : Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M(1;0) . Phép quay tâm O góc 90^o biến điểm M thành M’ có tọa độ là

A. (0;2) .

B. (0;1) .

C. (1;1) .

D. (2;0) .

Câu 2 : Phương trình  tương đương với phương trình nào sau đây ?

Câu 3 : Phương trình  có nghiệm là

Câu 4 : Khẳng định nào sau đây là sai ?

A. Hàm số y = x + xcos là hàm số chẵn.

B. Hàm số y = sinx là hàm số lẻ.

C. Hàm số y = cosx là hàm số chẵn.

D. Hàm số y = x + sinx là hàm số lẻ.

Câu 5 : Trong mặt phẳng với hệ tọa độ Oxy. Phép tịnh tiến theo vectơ  biến đường thẳng Δ: x – y -1 = 0 thành đường thẳng Δ’ có phương trình là

A.x – y – 1 = 0 .

B. x + y – 1 = 0 .

C. x – y – 2 = 0 .

D. x + y + 2 = 0 .

Câu 6 : Trong mặt phẳng với hệ tọa độ Oxy, điểm M(1;1) . Phép tịnh tiến theo vectơ  biến M thành điểm M’ có tọa độ là

A. (2;1)

B. (1;0)

C. (1;2)

D. (2;0)

Câu 7 : Trong các mệnh đề sau, mệnh đề nào đúng ?

A. Có đúng hai mặt phẳng đi qua một điểm và một đường thẳng cho trước.

B. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng không chứa điểm đó.

C. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng chứa điểm đó.

D. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng cho trước.

Câu 8 : Có 8 đội bóng chuyền nữ thi đấu theo thể thức vòng tròn (hai đội bóng chuyền bất kì chỉ gặp nhau một lần) và tính điểm. Số trận đấu được tổ chức là

A. 28.

B. 56.

C. 8.

D. 40320.

Câu 9 : Giả sử một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có  cách thực hiện, hành động kia có  cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất. Công việc đó có

A.  cách thực hiện.

B.  cách thực hiện.

C.  cách thực hiện.

D.  cách thực hiện.

Câu 10 : Kí hiệu  là số các tổ hợp chập k của n phần tử  . Khi đó  bằng

Câu 11 : Khẳng định nào sau đây là đúng?

Câu 12 : Từ các chữ số 1, 2,3, 4,5, 6, 7 và 8 lập được bao nhiêu số gồm 5 chữ số khác nhau đôi một?

A. 120.

B. 6720.

C. 7620.

D. 210.

Câu 13 : Số hạng chứa x trong khai triển của biểu thức (x + 1)⁶ là

A. 7x

B. 5x

C. 4x

D. 6x

Câu 14 : Tìm tập xác định D của hàm số 

Câu 15 : Tìm tập xác định D của hàm số 

Câu 16 : Số nghiệm của phương trình  với  là?

A. 2.

B. 4.

C. 6.

D. 7.

Câu 17 : Tập xác định của hàm số  là

Câu 18 : Trong mặt phẳng với hệ tọa độ Oxy . Phép tịnh tiến theo vectơ  biến đường tròn  thành đường tròn (C’) có phương trình

Câu 19 : Trong mặt phẳng với hệ tọa độ Oxy, điểm M(1;1) N(1;-1) . Phép tịnh tiến theo vectơ  biến M thành điểm N. Khi đó ta có

Câu 20 : Số vị trí biểu diễn các nghiệm của phương trình  trên đường tròn lượng giác là?

A.1

B. 2

C. 4

D. 6

Câu 21 : Tính tổng T các nghiệm của phương trình  trên khoảng 

Câu 22 : Tìm nghiệm dương nhỏ nhất  của 

Câu 23 : Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Một học sinh muốn chọn một đồ vật duy nhất hoặc một cây bút chì hoặc một cây bút bi hoặc một cuốn tập thì số cách chọn khác nhau là:

A. 480

B. 24

C. 48

D. 60

Câu 24 : Một bó hoa có 5 hoa hồng trắng, 6 hoa hồng đỏ và 7 hoa hồng vàng. Hỏi có mấy cách chọn lấy ba bông hoa có đủ cả ba màu.

A. 240

B. 210

C.18

D. 120

Câu 25 : Trong mặt phẳng với hệ tọa độ Oxy. Phép tịnh tiến theo vectơ  biến đường thẳng  thành đường thẳng  . Khi đó ta có

Câu 26 : Tìm mệnh đề sai trong các mệnh đề sau

A. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt

B. Nếu hai mặt phẳng có một điểm chung thì chúng còn vô số điểm chung nữa

C. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng

D. Nếu một đường thẳng có một điểm thuộc mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó

Câu 27 : Trong mặt phẳng với hệ tọa độ Oxy, phép vị tự tâm O tỉ số k = 2 biến đường thẳng  thành đường thẳng nào trong các đường thẳng có phương trình sau ?

Câu 28 : Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất hai lần. Xác suất để ít nhất một lần xuất hiện mặt hai chấm là :

Câu 29 : Giá trị lớn nhất của hàm số  là:

A. -7

B. -3

C. 3

D. -5

Câu 30 : Xếp 2 học sinh nam khác nhau và 2 học sinh nữ khác nhau vào một hàng ghế dài có 6 chỗ ngồi sao cho 2 học sinh nam ngồi kề nhau và 2 học sinh nữ ngồi kề nhau. Hỏi có bao nhiêu cách ?

A. 720.

B. 48.

C. 120.

D. 16.

Câu 31 : Lấy ngẫu nhiên một thẻ từ một hộp chứa 24 thẻ được đánh số từ 1 đến 24. Xác suất để thẻ lấy được ghi số chia hết cho 4 là :

Câu 32 : Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng (SAB) và (SCD) là:

A. Đường thẳng đi qua S và song song với đường thẳng AD

B. Đường thẳng đi qua S và song song với đường thẳng BD

C. Đường thẳng đi qua S và song song với đường thẳng AC

D. Đường thẳng đi qua S và song song với đường thẳng CD

Câu 33 : Trong mặt phẳng với hệ tọa độ Oxy, phép vị tự tâm I(1;2) tỉ số k biến điểm M(3;3) thành điểm M'(5;7) . Khi đó k bằng bao nhiêu?

A. 4.

B. 2.

C. 5.

D. 3.

Câu 34 : Biết hệ số của số hạng chứa x² trong khai triển của biểu thức  là 220. Tìm  ?

Câu 35 : Số hạng không chứa x trong khai triển của biểu thức  là:

Câu 36 : Phương trình  tương đương với phương trình

Câu 37 : Số nghiệm của phương trình  trên khoảng  là:

A. 7.

B. 5.

C. 8.

D. 6.

Câu 38 : Đề cương ôn tập cuối năm môn Toán lớp 11 có 50 câu hỏi. Đề thi cuối năm gồm 5 câu trong số 50 câu đó. Một học sinh chỉ ôn 25 câu trong đề cương. Giả sử các câu hỏi trong đề cương đều có khả năng được chọn làm câu hỏi thi như nhau. Xác suất để có ít nhất 3 câu hỏi của đề thi cuối năm nằm trong số 25 câu hỏi mà học sinh nói trên đã ôn tập là :

Câu 39 : Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho bạn An và bạn Dũng luôn ngồi ở hai đầu ghế?

A. 120

B. 16

C. 12

D. 24.

Câu 40 : Trên giá sách muốn xếp 20 cuốn sách khác nhau. Có bao nhiêu cách sắp xếp sao cho tập 1 và tập 2 không đặt cạnh nhau.

A. 20! – 18!

B.20!- 19!

C. 20!- 18!. 2!

D.19!. 18

Câu 41 : Một thùng có 7 sản phầm, trong đó có 4 sản phầm loại I và 3 sản phầm loại II. Lấy ngẫu nhiên 2 sản phẩm. Xác suất để lấy được 2 sản phẩm cùng loại là

Câu 42 : Số hạng không chứa x trong khai triển  là

Câu 43 : Cho tập A = {0,1,2……9} Số các số tự nhiên có 5 chữ số đôi một khác nhau lấy ra từ tập A là?

A. 30420

B.27162

C.27216

D.30240

Câu 44 : Có bao nhiêu số tự nhiên gồm 7 chữ số khác nhau đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3?

A. 249

B.7440

C.3204

D. 2942

Câu 45 : Trong một ban chấp hành đoàn gồm 7 người, cần chọn 3 người trong ban thường vụ. Nếu không có sự phân biệt về chức vụ của 3 người trong ban thường vụ thì có bao nhiêu các chọn?

A. 25

B. 30

C. 40

D. 35

Câu 46 : Trong mặt phẳng cho tập hợp P gồm 2018 điểm phân biệt. Hỏi có bao nhiêu đoạn thẳng mà hai đầu mút thuộc P ?

Câu 47 : Cho 10 điểm phân biệt A₁; A₂;….;A₁₀₀ trong đó có 4 điểm A₁;A₂;A₃;A₄ thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác có 3 đỉnh được lấy trong 10 điểm trên?

A. 96 tam giác.

B.60 tam giác.

C. 116 tam giác.

D. 80 tam giác.

Câu 48 : Cho hai đường thẳng song song d₁ và d₂ . Trên d₁ lấy 17 điểm phân biệt, trên d₂ lấy 20 điểm phân biệt. Tính số tam giác mà có các đỉnh được chọn từ 37 điểm này.

A. 5690

B. 5960

C. 5950

D. 5590

Câu 49 : Số giao điểm tối đa của 5 đường tròn phân biệt là:

A.10

B. 20

C. 18

D. 22

Câu 50 : Trong các mệnh đề sau, mệnh đề nào đúng?

A. Phép đối xứng trục là phép đồng nhất

B. Thực hiện liên tiếp phép quay và phép vị tự ta được phép đồng dạng.

C. Phép đồng dạng là một phép dời hình.

D. Phép vị tự là một phép dời hình.

Đáp án và Hướng dẫn làm bài

Câu 1 : Chọn B

Câu 2 : Chọn D

Câu 3 : Chọn D

Câu 4 : Chọn A

Xét phương án A:

Ta có

Do đó; hàm số y = x + cosx là hàm số không chẵn; không lẻ

Câu 5 : Chọn A

Ta có: 

Vì điểm M thuộc đường thẳng Δ nên : x – y – 1 = 0 (*)

Thay vào (*) ta được:

Câu 6 : Chọn C

Ta có:

Câu 7 : Chọn B

Ta có A sai vì nếu điểm đó thuộc đường thẳng thì sẽ có vô số mặt phẳng.

+) B đúng

+) C sai (suy ra từ A).

+) D sai (suy ra từ A).

Câu 8 : Chọn A

Số trận đấu được tổ chức là: 

Câu 9 : Chọn C

Công việc đó có m + n cách thực hiện.

Câu 10 : Chọn D

Câu 11 : Chọn C

Hàm số y = cotx nghịch biến trên khoảng 

Câu 12 : Chọn B

Gọi số có 5 chữ số thỏa mãn đầu bài là: 

+ chọn a có 8 cách

+ Chọn b: có 7 cách

+ Chọn c có 6 cách

+ Chọn d co 5 cách

+ Chọn e có 4 cách

Theo quy tắc nhân có 8.7.6.5.4 = 6720 số thỏa mãn.

Câu 13 : Chọn D

Ta có

Số hạng chứa x cần thỏa mãn:

6 – k = 1 ⇒ k = 5

Vậy số hạng chứa x là: 

Câu 14 : Chọn A

Hàm số xác định khi và chỉ khi các điều kiện sau thỏa mãn đồng thời

 , xác định và cot x xác định.

Ta có 

⇒ 

 xác định ⇔ 

cot x xác định 

Do đó hàm số xác định 

Vậy tập xác định 

Câu 15 : Chọn D

Hàm số xác định khi và chỉ khi  .

Do 

Vậy tập xác định 

Câu 16 : Chọn B

Vậy có tất cả 4 nghiệm thỏa mãn bài toán.

Câu 17 : Chọn A

Điều kiện: 

Câu 18 : Chọn C

Câu 19 : Chọn D

Ta có : 

Câu 20 : Chọn C

Câu 21 : Chọn C

Câu 22 : Chọn B

So sánh hai nghiệm ta được nghiệm dương nhỏ nhất là 

Câu 23 : Chọn B

Nếu chọn một cây bút chì thì sẽ có 8 cách.

Nếu chọn một cây bút bi thì sẽ có 6 cách.

Nếu chọn một cuốn tập thì sẽ có 10 cách.

Theo qui tắc cộng, ta có 8+ 6 + 10 = 24cách chọn.

Câu 24 : Chọn B

Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có:

Có 5 cách chọn hoa hồng trắng.

Có 6 cách chọn hoa hồng đỏ.

Có 7 cách chọn hoa hồng vàng.

Vậy theo qui tắc nhân ta có 5.6.7 = 210 cách.

Câu 25 : Chọn C

Lấy A(1;1)∈ d và vectơ 

Ta có 

Vì A’ thuộc d’ suy ra a + 1 + 2(b + 1) – 7 = 0 ⇔ a + 2ab = 4 .

Trong các phương án chỉ có phương án C thỏa mãn

Câu 26 : Chọn D

Mệnh đề: A, B, C đúng.

Mệnh đề D chỉ đúng khi đường thẳng nằm trong mặt phẳng , còn khi đường thẳng cắt mặt phẳng tại một điểm thì mệnh đề trên là sai .

Câu 27 : Chọn B

Gọi d’: x + y + m = 0 là ảnh của d’ qua phép vị tự tâm O.

Vì O ∈ d suy ra O chính là ảnh của O qua V_(O;k) .

Vậy (d’): x + y = 0 .

Câu 28 : Chọn A

TH1: Gieo lần 1 xuất hiện mặt 2 chấm, lần 2 không xuất hiện mặt 2 chấm ⇒ có 5 cách.

TH2: Gieo lần 1 không xuất hiện mặt 2 chấm, lần 2 xuất hiện mặt 2 chấm ⇒ có 5 cách.

TH3: Gieo cả 2 lần đều được mặt 2 chấm ⇒ có 1 cách.

Vậy xác suất cần tính là  .

Câu 29 : Chọn A

Vậy y_max = -3

Câu 30 : Chọn B

Coi 2 bạn nam ngồi cạnh nhau là 1 phần tử X, 2 bạn nữ ngồi cạnh nhau là 1 phần tử Y.

Chọn 2 ghế từ 4 ghế để xếp 2 phần tử X; Y có:  cách

Đổi chỗ 2 bạn nữ ta có them 1 cách. Nên số cách xếp 2 bạn nữ trong Y là 2.

Số cách xếp 2 bạn nam trong X là 2

Theo quy tắc nhân, có tất cả  cách.

Câu 31 : Chọn

Lấy ngẫu nhiên 1 thẻ trong 24 thẻ có 24 cách suy ra n(Ω) = 24 .

Trong các số từ 1 đến 24 có số {4;8;12;16;20;24} chia hết cho 4.

Suy ra số kết quả thuận lợi cho biến cố là n(X) = 6 .

Vậy 

Câu 32 : Chọn D

Xét giao tuyến của 2 mặt phẳng ( SAB) và (SCD) có:

S chung

AB// CD

AB ⊂ (SAB) ; CD ⊂ (SCD)

Suy ra giao tuyến của hai mặt phẳng (SAB), (SCD) là đường thẳng đi qua S và song song với đường thẳng CD.

Câu 33 : Chọn D

Câu 34 : Chọn A

Câu 35 : Chọn D

Ta có 

Số hạng không chứa x khi k = 10 , hệ số của nó là  .

Câu 36 : Chọn C

Câu 37 : Chọn A

Câu 38 : Chọn C

Không gian mẫu là 

Giả sử trong 25 câu có 3 câu hỏi đề thi:  .

Giả sử trong 25 câu có 4 câu hỏi đề thi: 

Giả sử trong 25 câu có 5 câu hỏi đề thi: 

Xác suất cần tìm là: 

Câu 39 : Chọn C

Xếp An và Dũng ngồi hai đầu ghế có 2! cách xếp.

Số cách xếp 3 bạn Bình, Chi, Lệ vào 3 ghế còn lại là một hoán vị của 3 phần tử nên có có 3! cách.

Vậy có 2!.3! = 12 cách.

Câu 40 : Chọn D

• Sắp xếp 20 cuốn sách trên giá là một hoán vị của 20 phần tử nên ta có

20! cách sắp xếp.

• Khi hai cuốn tập 1 và tập 2 đặt cạnh nhau (thay đổi vị trí cho nhau), ta coi đó là một phần tử và cùng sắp xếp với 18 cuốn sách còn lại trên giá nên có 2. 19! cách sắp xếp.

Vậy có tất cả 20! – 2.19! = 19!.18 cách sắp xếp theo yêu cầu bài toán.

Câu 41 : Chọn B

Không gian mẫu là 

Không gian biến cố là 

Câu 42 : Chọn C

Ta có 

Số hạng không chứa x khi 

Câu 43 : Chọn C

Gọi số cần tìm là  .

Chọn a có 9 cách.

Chọn b; c; d; e từ 9 số còn lại có  = 3024 cách.

Vậy có 9. 3024 = 27216.

Câu 44 : Chọn B

Ta chia thành các trường hợp sau:

TH1: Nếu số 123 đứng đầu thì có  số.

TH2: Nếu số 321 đứng đầu thì có  số.

TH3: Nếu số 123; 321 không đứng đầu

Khi đó có 6 cách chọn số đứng đầu ( khác 0; 1; 2; 3 ).

khi đó còn 6 vị trí:

có 4 cách xếp 3 số 321 hoặc 123, còn lại 3 vị trí có  cách chọn các số còn lại.

Do đó trường hợp này có 6.2.4. = 5760

Suy ra tổng các số thoả mãn yêu cầu là 2. + 5760 = 7440 .

Câu 45 : Chọn D

Vì không xét đến sự phân biệt chức vụ của 3 người trong ban thường vụ nên mỗi cách chọn ứng với một tổ hợp chập 3 của 7 phần tử.

Như vậy, ta có  = 35 cách chọn ban thường vụ.

Câu 46 : Chọn D

Với hai điểm bất kỳ trong n điểm ta luôn được một đoạn thẳng.

Vậy số đoạn thẳng cần tìm chính là một tổ hợp chập 2 của 2018 phần tử (điểm).

Như vậy, ta có  đoạn thẳng.

Câu 47 : Chọn C

Số cách lấy 3 điểm từ 10 điểm phân biệt là 

Số cách lấy 3 điểm bất kì trong 4 điểm A₁ ; A₂ ; A₃ ; A₄ là 

Khi lấy 3 điểm bất kì trong 4 điểm A₁ ; A₂ ; A₃ ; A₄ thì sẽ không tạo thành tam giác.

Như vậy, số tam giác tạo thành 120 – 4 = 116 tam giác.

Câu 48 : Chọn C

Một tam giác được tạo bởi ba điểm phân biệt nên ta xét:

TH1. Chọn 1 điểm thuộc d₁ và 2 điểm thuộc d₂ có  tam giác.

TH2. Chọn 2 điểm thuộc d₁ và 1 điểm thuộc d₂ có  tam giác.

Như vậy, ta có  tam giác cần tìm.

Câu 49 : Chọn B

Hai đường tròn cho tối đa hai giao điểm.

Và 5 đường tròn phân biệt cho số giao điểm tối đa khi 2 đường tròn bất kỳ trong 5 đường tròn đôi một cắt nhau.

Vậy số giao điểm tối đa của 5 đường tròn phân biệt là 

Câu 50 : Chọn B