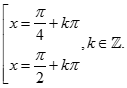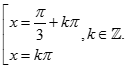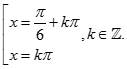MA TRẬN VÀ ĐỀ THI GIỮA HỌC KÌ TOÁN 11
KHUNG MA TRẬN
– Trắc nghiệm: 15 câu x 1/3 điểm= 5,0 điểm;
|
Bài / Chủ đề |
Cấp độ tư duy |
Cộng |
|||||||
|
Nhận biết |
Thông hiểu |
Vận dụng thấp |
Vận dụng cao |
||||||
|
TN |
TL |
TN |
TL |
TN |
TL |
TN |
TL |
|
|
|
Các hàm số lượng giác |
Câu 1, Câu 2 |
|
Câu 3 |
|
|
|
|
|
Đại số 65% |
|
Phương trình lượng giác |
Câu 4 |
Bài 1a |
|
|
Câu 5 |
|
|
Bài 1b |
|
|
Quy tắc đếm |
Câu 6, Câu 7 |
|
|
|
Câu 8 |
Bài 2b |
|
|
|
|
Hoán vị, chỉnh hợp, tổ hợp |
Câu 9 |
|
|
Bài 2a |
|
|
|
|
|
|
Phép tịnh tiến |
Câu 10 |
|
|
Bài 3a |
Câu 11 |
|
|
|
Hình học 35% |
|
Phép quay |
Câu 12 |
|
Câu 13, Câu14 |
|
|
|
|
|
|
|
Phép vị tự |
Câu 15 |
|
|
Bài 3b |
|
|
|
|
|
|
Cộng |
9 câu (3,0 đ) |
1 câu (1,0 đ) |
3 câu (1,0 đ) |
3 câu (2,0 đ) |
3 câu (1,0 đ) |
1 câu (1,0 đ) |
|
1 câu (1,0 đ) |
|
|
40% |
30% |
20% |
10% |
100% |
|||||
2. BẢNG MÔ TẢ CHI TIẾT NỘI DUNG CÂU HỎI
|
CHỦ ĐỀ |
CÂU |
MỨC ĐỘ |
MÔ TẢ |
|
Các hàm số lượng giác |
1 |
NB |
Tính chẵn lẻ, chu kì tuần hoàn của các hàm số lượng giác. |
|
2 |
NB |
Tìm tập giá trị của các hàm số lượng giác. |
|
|
3 |
TH |
Tìm tập xác định của các hàm số lượng giác. |
|
|
Phương trình lượng giác |
4 |
NB |
Tìm nghiệm của phương trình lượng giác cơ bản. |
|
1a(TL) |
NB |
[1.0đ] Giải phương trình lượng giác cơ bản. |
|
|
5 |
VDT |
Giải phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác. |
|
|
1b(TL) |
VDC |
[1.0đ] Tổng hợp về phương trình lượng giác. |
|
|
Qui tắc đếm |
6 |
NB |
Áp dụng các quy tắc đếm. |
|
7 |
NB |
Áp dụng các quy tắc đếm. |
|
|
8 |
VDT |
Áp dụng quy tắc đếm để giải các bài toán liên quan |
|
|
2b(TL) |
VDT |
[1,0đ] Bài toán tổng hợp liên quan qui tắc đếm. |
|
|
Hoán vị, chỉnh hợp, tổ hợp |
9 |
NB |
Định nghĩa và tính chất của hoán vị, chỉnh hợp, tổ hợp. |
|
2b(TL) |
TH |
[0.5đ] Áp dụng các công thức về số hoán vị, hoặc số chỉnh hợp, hoặc số tổ hợp. |
|
|
Phép tịnh tiến |
10 |
NB |
Tính chất của phép tịnh tiến. |
|
11 |
VDT |
Tìm vectơ tịnh tiến. |
|
|
3a(TL) |
TH |
[0.75đ] Tìm ảnh của đường thẳng (đường tròn) qua phép tịnh tiến. |
|
|
Phép quay |
12 |
NB |
Tìm ảnh của điểm qua phép quay, phép tịnh tiến, phép vị tự. |
|
13 |
TH |
Tìm được ảnh của đường thẳng (đường tròn) qua phép quay, phép tịnh tiến, phép vị tự. |
|
|
14 |
TH |
Xác định góc quay. |
|
|
Phép vị tự |
15 |
NB |
Tính chất của phép vị tự. |
|
3b(TL) |
TH |
[0.75đ] Tìm ảnh của đường tròn (đường thẳng) qua phép vị tự trong mặt phẳng toạ độ. |
Đề thi Toán lớp 11 Giữa học kì 1 năm 2022 có ma trận (18 đề) – Đề 1
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa Học kì 1
Năm học 2022 – 2023
Bài thi môn: Toán lớp 11
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 1)
Câu 1: Hàm số nào dưới đây là hàm số chẵn ?
|
A. |
B. |
C. |
D. |
Câu 2: Tập xác định hàm số 
là:
|
A. |
B. |
|
C. |
D. |
Câu 3: Tập giá trị của hàm số 
là
|
A. |
B. |
C. |
D. |
Câu 4: Hàm số 
là hàm số tuần hoàn với chu kì bằng
|
A. |
B. |
C. |
D. |
Câu 5: Hàm số nào dưới đây có đồ thị là đường cong như trong hình bên ?
A. 
B. 
C. 
D. 
Câu 6: Tập hợp tất cả các giá trị của tham số m để phương trình 
có nghiệm là
|
A. |
B. |
C. |
D. |
Câu 7: Nghiệm của phương trình 
là
|
A. |
B. |
|
C. |
D. |
Câu 8: Nghiệm của phương trình 
là
|
A. |
B. |
|
C. |
D. |
Câu 9: Nghiệm của phương trình 
là
|
A. |
B. |
|
C. |
D. |
Câu 10: Nghiệm của phương trình 
là
|
A. |
B. |
|
C. |
D. |
Câu 11: Có bao nhiêu cách chọn ra một cái bút từ 3 cái bút bi khác nhau và 2 cái bút chì khác nhau ?
|
A.5 |
B. 6 |
C.3 |
D.2 |
Câu 12: Đội cầu lông của tỉnh A có 4 vận động viên nam và 5 vận động viên nữ. Hỏi tỉnh A có bao nhiêu cách chọn ra một đôi nam nữ để đi thi đấu?
|
A.20 |
B.9 |
C.4 |
D.5 |
Câu 13: Với k và n là hai số nguyên tùy ý thỏa mãn 
mệnh đề nào dưới đây đúng ?
|
A. |
B. |
|
C. |
D. |
Câu 14: Có bao nhiêu cách xếp 4 học sinh thành một hàng dọc ?
|
A.24 |
B.4 |
C.10 |
D.20 |
Câu 15: 
bằng
|
A.60 |
B.30 |
C.120 |
D.15 |
Câu 16: Trong mặt phẳng Oxy với vectơ 
tùy ý và điểm 
gọi điểm 
là ảnh của M qua phép tịnh tiến theo vectơ 
. Mệnh đề nào dưới đây đúng ?
|
A. |
B. |
C. |
D. |
Câu 17: Ảnh của một đường tròn có bán kính bằng 2 qua phép đối xứng trục là một đường tròn có bán kính bằng bao nhiêu ?
|
A.2 |
B.1 |
C.4 |
D. |
Câu 18: Trong mặt phẳng, cho hai điểm phân biệt A,B. Biết rằng phép đối xứng tâm I biến A thành B. Mệnh đề nào dưới đây đúng?
A. Điểm I là trung điểm của đoạn thẳng AB
B. Điểm A trùng với điểm B
C. Điểm A là trung điểm của đoạn thẳng IB
D. Điểm B là trung điểm của đoạn thẳng IA
Câu 19: Trong mặt phẳng, cho tam giác ABC vuông. Phép dời hình biến tam giác ABC thành tam giác A’B’C’. Mệnh đề nào dưới đây đúng ?
A. Tam giác A’B’C’ là tam giác vuông.
B. Tam giác A’B’C’ là tam giác nhọn.
C. Tam giác A’B’C’ là tam giác đều.
D. Tam giác A’B’C’ là tam giác tù.
Câu 20: Ảnh của đường tròn có bán kính bằng 2 qua phép vị tự tâm I tỉ số k=2 là đường tròn có bán kính bằng bao nhiêu ?
|
A. 4 |
B. 2 |
C. 1 |
D. |
Câu 21: Hàm số nào dưới đây có tập xác định là R?
|
A. |
B. |
|
C. |
D. |
Câu 22: Nghiệm của phương trình 
là
|
A. |
B. |
|
C. |
D. |
Câu 23: Nghiệm của phương trình 
là
|
A. |
B. |
|
C. |
D. |
Câu 24: Nghiệm của phương trình 
là
|
A. |
B. |
|
C. |
D. |
Câu 25: Nghiệm của phương trình 
là
|
A. |
B. |
|
C. |
D. |
Câu 26: Nghiệm của phương trình 
là
|
A. |
B. |
|
C. |
D. |
Câu 27: Từ các chữ số 
có thể lập được bao nhiêu số tự nhiên có 3 chữ số ?
|
A.216 |
B.120 |
C.18 |
D.10 |
Câu 28: Từ các chữ số 
có thể lập được bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau ?
|
A.120 |
B.216 |
C.18 |
D.10 |
Câu 29: Một hộp chứa 5 quả cầu đỏ khác nhau và 3 quả cầu xanh khác nhau. Có bao nhiêu cách chọn ra 2 quả cầu cùng màu ?
|
A.13 |
B.8 |
C.15 |
D.30 |
Câu 30: Có bao nhiêu cách chọn 2 học sinh từ một nhóm gồm 10 học sinh ?
|
A.45 |
B.90 |
C.100 |
D.10 |
Câu 31: Trong mặt phẳng 0xy cho vectơ 
và điểm 
Phép tịnh tiến theo vectơ 
biến A thành điểm A’ tọa độ của A’ là
|
A. |
B. |
C. |
D. |
Câu 32: Trong mặt phẳng )xy cho đường thẳng 
Phép đối xứng qua trục Ox biến 
thành đường thẳng 
phương trình của 
là
|
A.x-y-3=0 |
B.x+y-3=0 |
C.-x+y-3=0 |
D.x+y+3=0 |
Câu 33: Trong mặt phẳng 0xy cho điểm 
Phép đối xứng tâm O biến A thành điểm A’ tọa độ của A’ là
A.
B.
C.
D.
Câu 34: Cho hình vuông 
có tâm như hình vẽ bên. Ảnh của điểm M qua phép quay tâm 0 góc quay 90 là điểm nào dưới đây ?
A. Điểm Q
B. Điểm P
C. Điểm M
D. Điểm N
Câu 35: Cho tam giác ABC có trọng tâm G. Gọi các điểm A’, B’, C’ lần lượt là trung điểm của các cạnh 
Biết rằng phép vị tự tâm G tỉ số k biến tam giác ABC thành tam giác A’B’C’ giá trị của bằng
|
A. |
B. |
C.2 |
D.-2 |
PHẦN TỰ LUẬN
Câu 1: Giải phương trình 
Câu 2: Trong mặt phẳng Oxy cho vectơ 
và đường thẳng 
Phép tịnh tiến theo vectơ 
biến 
thành đường thẳng 
viết phương trình của 
Câu 3: a) Từ các chữ số 
lập được bao nhiêu số tự nhiên có bốn chữ số khác nhau và số đó lớn hơn 2020
b) Cho đa giác lồi H có cạnh. Có bao nhiêu tam giác mà mỗi đỉnh của nó là đỉnh của H và mỗi cạnh của tam giác đó không trùng với cạnh nào của H
Đề thi Toán lớp 11 Giữa học kì 1 năm 2022 có ma trận (18 đề) – Đề 2
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa Học kì 1
Năm học 2022 – 2023
Bài thi môn: Toán lớp 11
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 2)
Câu 1: Nghiệm của phương trình 
là
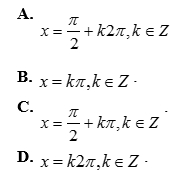
Câu 2: Trong mặt phẳng, cho ba điểm O, M, N không thẳng hàng và 
. Mệnh đề nào sau đây là sai ?
A. OM’N’ = OMN.
B. OM’ = OM.
C. M’N’ = MN.
D. 
.
Câu 3: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng 
. Viết phương trình đường thẳng d’ là ảnh của đường thẳng d qua phép quay tâm O, góc quay 90.
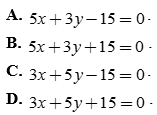
Câu 4: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(1;2), B(5; -1). Gọi A’, B’ lần lượt là ảnh của A, B qua phép quay tâm O góc quay 900. Tính độ dài đoạn thẳng A’B’.
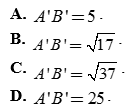
Câu 5: Cho hai số tự nhiên k, n thỏa 
. Mệnh đề nào sau đây đúng ?
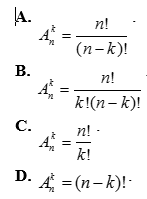
Câu 6: Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn 
. Ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ 
là đường tròn 
Khi đó tọa độ của vectơ là
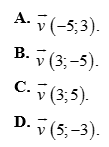
Câu 7: Phương trình 
có bao nhiêu nghiệm trong khoảng 
?
A. 8.
B. 4.
C. 2 .
D. 6.
Câu 8: Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số 
.
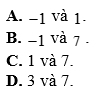
Câu 9: Có bao nhiêu số tự nhiên có 5 chữ số khác nhau sao cho tổng 2 chữ số cách đều chữ số đứng chính giữa là bằng nhau và bằng 5?
A. 120.
B. 24.
C. 20.
D. 144.
Câu 10: Tìm tập xác định của hàm số 
.
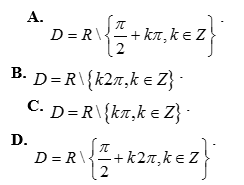
Câu 11: Trong mặt phẳng với hệ tọa độ Oxy, cho vectơ 
, điểm M(4; 3). Tìm tọa độ điểm M’ là ảnh của điểm M qua phép tịnh tiến theo vectơ v.
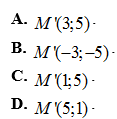
Câu 12: Một người có 4 cái áo khác màu nhau và 5 cái quần khác màu nhau. Hỏi người này có bao nhiêu cách chọn một bộ áo quần để mặc đi dự tiệc ?
A. 9.
B. 20.
C. 45 .
D. 54.
Câu 13: Một cô gái có 2 cái mũ màu trắng, 3 cái mũ màu xanh và 5 cái mũ màu vàng, tất cả các cái mũ đều khác kiểu. Hỏi cô gái này có bao nhiêu cách chọn một cái mũ để đội đi dạo ?
A. 10.
B. 5.
C. 30.
D. 6.
Câu 14: Mệnh đề nào sau đây đúng ?
Câu 15: Trong mặt phẳng, cho đoạn thẳng AB có trung điểm I và phép vị tự tâm A, tỉ số k. Biết 
, tìm tỉ số vị tự k.
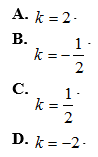
II. Tự luận (5 điểm)
Bài 1. (2.0 điểm) Giải các phương trình sau:
a) 
.
b) 
.
Bài 2. (1.5 điểm)
a) Một hộp đựng 9 viên bi khác nhau, trong đó có 5 viên bi xanh và 4 viên bi đỏ. Có bao nhiêu cách chọn từ hộp đó ra 3 viên bi gồm 2 viên bi xanh và 1 viên bi đỏ?
b) Cho tập hợp 
. Có bao nhiêu số tự nhiên gồm 5 chữ số được lập từ sao cho tích các chữ số bằng 630 ?
Bài 3. (1.5 điểm) Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng 
và đường tròn 
a) Viết phương trình đường thẳng ảnh của (d) qua phép tịnh tiến theo vectơ 
.
b) Viết phương trình đường tròn ảnh của (C) qua phép vị tự tâm O, tỉ số k=2.
Đề thi Toán lớp 11 Giữa học kì 1 năm 2022 có ma trận (18 đề) – Đề 3
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa Học kì 1
Năm học 2022 – 2023
Bài thi môn: Toán lớp 11
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 3)
TRẮC NGHIỆM: (5,0 điểm)
Câu 1: Tìm mệnh đề sai trong các mệnh đề sau:
A. y = cosx là hàm số tuần hoàn chu kì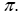
B. y = tanx là hàm số tuần hoàn chu kì
C. y = sin x là hàm số tuần hoàn chu kì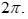
D. y = cotx là hàm số tuần hoàn chu kì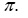
Câu 2: Tập giá trị của hàm số y = cosx là
A. [-1;1] . B.(-1;1) .
C.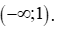
. D. R .
Câu 3: Hàm số y = tanx có tập xác định là:
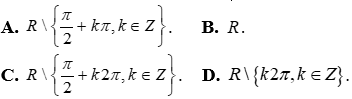
Câu 4: Giải phương trình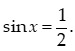
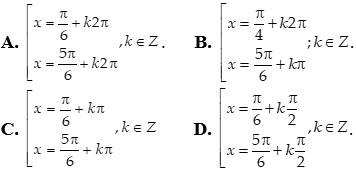
Câu 5: Giải phương trình 4cosx – sin2x = 0.
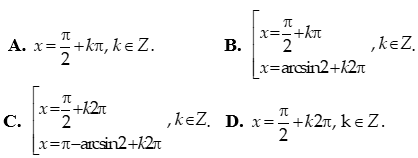
Câu 6: Từ thành phố A đến thành phố B có 5 con đường, từ thành phố B đến thành phố C có 3 con đường. Hỏi có bao nhiêu cách đi từ A đến C, phải qua B?
A. 15. B. 12.
C. 8. D. 6.
Câu 7: Từ các chữ số 1, 2, 3, 4 có thể lập được bao nhiêu số tự nhiên có ba chữ số?
A. 64. B. 12.
C. 24. D. 50.
Câu 8: Có 3 học sinh nữ và 2 học sinh nam. Ta muốn sắp xếp số học sinh đó vào một bàn dài có 5 ghế ngồi. Có bao nhiêu cách sắp xếp để 2 học sinh nam ngồi kề nhau?
A. 48. B. 42.
C. 58. D. 12.
Câu 9: Mệnh đề nào sau đây là đúng?
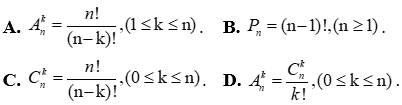
Câu 10: Trong mặt phẳng, cho phép tịnh tiến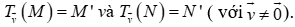
Mệnh đề nào sau đây là sai?
Câu 11: Trong mặt phẳng tọa độ Oxy , cho đường thẳng d:3x + y – 9 = 0. Phép tịnh tiến theo vectơ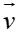
có giá song song với Oy , biến d thành d’ sao cho A(1;1) ∈ d’. Tọa độ của vectơ
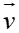là:
Câu 12: Trong mặt phẳng Oxy cho điểm A(3;0). Tìm tọa độ ảnh A’ của điểm A qua phép quay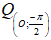
?
Câu 13: Tìm ảnh của đường thẳng d: 5x – 3y + 15 qua phép quay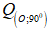
.
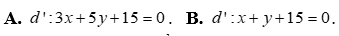
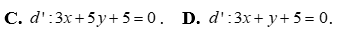
Câu 14: Trong mặt phẳng với hệ tọa độ Oxy , cho hai đường thẳng a và b có phương trình lần lượt là 4x + 3y – 2 = 0 và x + 7y – 4 = 0 Gọi phép quay biến đường thẳng này thành đường thẳng kia là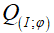 
. Tìm số đo của góc quay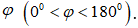
A. 45o. B. 60o.
C. 90o. D. 120o.
Câu 15: Tìm mệnh đề sai trong các mệnh đề sau: Phép vị tự tỉ số k
A. Biến tam giác thành tam giác bằng nó.
B. Biến tâm vị tự thành chính nó.
C. Biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
D. Biến đường tròn bán kính thành đường tròn bán kính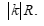
TỰ LUẬN: (5,0 điểm)
Câu 1 (2,0 điểm). Giải các phương trình lượng giác sau:
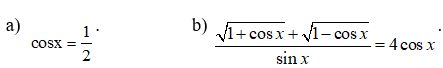
Câu 2 (2,5 điểm.) Cho tập hợp A = .
a) Có bao nhiêu số tự nhiên gồm 5 chữ số khác nhau được lập ra từ A ?
b) Có bao nhiêu số chẵn có 5 chữ số và các chữ số đó phải khác nhau được lập ra từ A ?
Câu 3:(1,5 điểm)
a) Trong mặt phẳng Oxy, ảnh của đường tròn: (x – 2)2 + (y – 1)2 = 16. Tìm ảnh của (C) qua phép tịnh tiến theo vectơ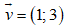
.
b) Trong măt phẳng Oxy, cho đường thẳng d có phương trình 2x + y – 3 = 0. Tìm ảnh của đường thẳng d qua phép vị tự tâm O tỉ số k = 2 .
Đề thi Toán lớp 11 Giữa học kì 1 năm 2022 có ma trận (18 đề) – Đề 4
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa Học kì 1
Năm học 2022 – 2023
Bài thi môn: Toán lớp 11
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 4)
TRẮC NGHIỆM: (5,0 điểm)
Câu 1: Trong các hàm số sau, hàm số nào chẵn?
A. y = cosx.
B. y = sinx.
C. y = cotx.
D. y=tanx.
Câu 2: Tập giá trị của hàm số y = cosx là:
A. [-1;1]
B. (-1;1)
C. (- ∞;1)
D. R.
Câu 3: Hàm số có tập xác định là:
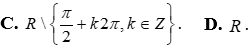
Câu 4: Giải phương trình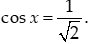 
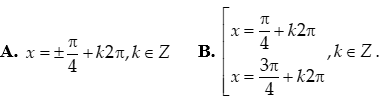
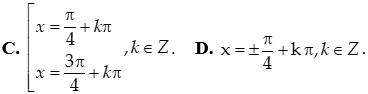
Câu 5: Giải phương trình 3cosx – sin2x = 0
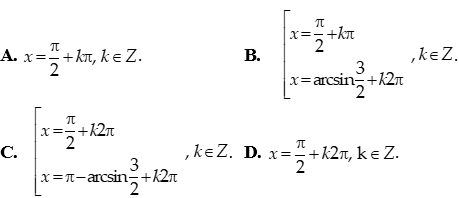
Câu 6: Từ thành phố A đến thành phố B có 3 con đường, từ thành phố B đến thành phố C có 4 con đường. Hỏi có bao nhiêu cách đi từ A đến C, phải qua B?
A. 12. B. 7.
C. 8. D. 6.
Câu 7: Từ các chữ số 1, 2,3 ,4, 5 có thể lập được bao nhiêu số tự nhiên có ba chữ số?
A. 125. B. 120.
C. 100. D. 60.
Câu 8: Có 3 học sinh nữ và 2 học sinh nam. Ta muốn sắp xếp số học sinh đó vào một bàn dài có 5 ghế ngồi. Hỏi có bao nhiêu cách sắp xếp để 3 học sinh nữ ngồi kề nhau ?
A. 36. B. 12.
C. 7. D. 6
Câu 9: Mệnh đề nào sau đây là đúng?
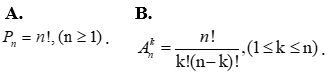
Câu 10: Tìm mệnh đề sai trong các mệnh đề sau:
A. Phép tịnh tiến biến đường tròn bán kính thành đường tròn có bán kính .
B. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.
C. Phép tịnh tiến biến tam giác thành tam giác bằng nó.
D. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
Câu 11: Trong mặt phẳng tọa độ Oxy , cho đường thẳng ∆: X + 2Y – 4 = 0. Phép tịnh tiến theo vectơ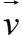
có giá song song với Ox , biến ∆ thành ∆’ sao cho A(-1;1) ∈ ∆’. Tìm tọa độ của vectơ
.
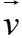Câu 12: Trong mặt phẳng Oxy cho điểm A(3;0) . Tìm tọa độ ảnh A’ của điểm A qua phép quay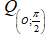
.
Câu 13: Tìm ảnh của đường thẳng d:x -3y + 9 = 0 qua phép quay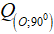
.
A. d’: 3x + y + 9 = 0
B. d’: x + 3y + 1 = 0
C. d’: x – 3y + 9 = 0
D. d’: 3x + y +5 = 0
Câu 14: Trong mặt phẳng với hệ tọa độ Oxy cho hai đường thẳng a và b có phương trình lần lượt là 2x + y + 5 = 0 và x – 2y – 3 = 0 Gọi phép quay biến đường thẳng này thành đường thẳng kia là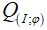 
. Tìm số đo của góc quay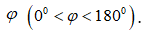
A. 90o B. 45o
C. 60o D. 120o
Câu 15: Nếu phép vị tự tỉ số k biến hai điểm M, N tùy ý theo thứ tự thành M’, N’ thì mệnh đề nào sau đây đúng?
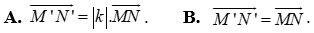
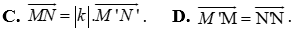
TỰ LUẬN: (5,0 điểm)
Câu 1 (2 điểm). Giải các phương trình lượng giác sau:
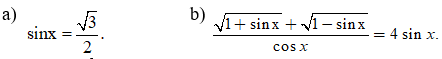
Câu 2 (1,5 điểm). Cho tập hợp A = .
a) Có bao nhiêu số tự nhiên gồm 4 chữ số khác nhau được lập ra từ A ?
b) Có bao nhiêu số chẵn có 4 chữ số và các chữ số đó phải khác nhau được lập ra từ A ?
Câu 3 (1,5 điểm).
a) Trong mặt phẳng Oxy, cho đường tròn (C) có phương trình x2 + y2 + 2x – 4y – 4 = 0 . Tìm ảnh của (C) qua phép tịnh tiến theo vectơ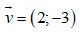
.
b) Trong măt phẳng Oxy, cho đường thẳng d có phương trình x + y – 2 = 0 . Tìm ảnh của đường thẳng d qua phép vị tự tâm O tỉ số k = – 2.