Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Bài tập trắc nghiệm hai mặt phẳng vuông góc có đáp án và lời giải
HAI MẶT PHẲNG VUÔNG GÓC
A. CÂU HỎI
Dạng 1. Câu hỏi lý thuyết
Câu 1. Khẳng định nào sau đây đúng?
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
C. Hai mặt phẳng song song khi và chỉ khi góc giữa chúng bằng 00.
D. Hai đường thẳng trong không gian cắt nhau khi và chỉ khi góc giữa chúng lớn hơn 00 và nhỏ hơn 900.
Câu 2. Chọn mệnh đề đúng trong các mệnh đề sau:
A. Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng tùy ý nằm trong mỗi mặt phẳng.
B. Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
C. Góc giữa hai mặt phẳng luôn là góc nhọn.
D. Góc giữa hai mặt phẳng bằng góc giữa hai vec tơ chỉ phương của hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Câu 3. Trong các mệnh đề dưới đây, mệnh đề nào sai?
A. Hình chóp tứ giác đều có tất cả các cạnh bằng nhau.
B. Hình chóp tứ giác đều có các cạnh bên bằng nhau.
C. Hình chóp tứ giác đều có đáy là hình vuông.
D. Hình chóp tứ giác đều có hình chiếu vuông góc của đỉnh lên đáy trùng với tâm của đáy.
Câu 4. Cho các đường thẳng a b, và các mặt phẳng (a), (b). Chọn mệnh đề đúng trong các mệnh đề sau
A. \[\left\{ {\begin{array}{*{20}{c}}{a \bot (\alpha )}\\{a \subset (\beta )}\end{array} \Rightarrow (\alpha ) \bot (\beta ).} \right.\]
B.
C. \[\left\{ {\begin{array}{*{20}{c}}{a \bot b}\\\begin{array}{l}a \subset (\alpha )\\b \subset (\beta )\end{array}\end{array} \Rightarrow (\alpha ) \bot (\beta ).} \right.\]
D. \[\left\{ {\begin{array}{*{20}{c}}{(\alpha ) \bot (\beta )}\\\begin{array}{l}a \subset (\alpha )\\b \subset (\beta )\end{array}\end{array} \Rightarrow a \bot b.} \right.\]
Câu 5. Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Cho hai mặt phẳng vuông góc với nhau, nếu một đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng thì vuông góc với mặt phẳng kia.
B. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước
C. Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
D. Đường thẳng d là đường vuông góc chung của hai đườngthẳng chéo nhau a, b khi và chỉ khi d vuông góc với cả a và b.
Câu 6. Cho đường thẳng a không vuông góc với mặt phẳng (a). Có bao nhiêu mặt phẳng chứa a và vuông góc với (a) .
A. 2 .
B. 0 .
C. Vô số.
D. 1.
Câu 7. Mảnh bìa phẳng nào sau đây có thể xếp thành lăng trụ tứ giác đều?
A. 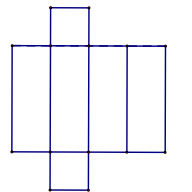
B. 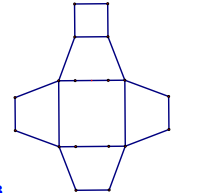
C. 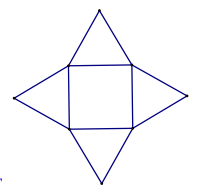
D. 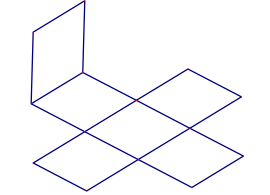
Câu 8. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu một đường thẳng nằm trong mặt phẳng này và vuông góc với mặt phẳng kia thì hai mặt phẳng vuông góc nhau.
B. Nếu hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì chúng song song với nhau.
C. Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này đều vuông góc với mặt phẳng kia.
D. Nếu hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì chúng vuông góc với nhau.
Câu 9. Cho đường thẳng a không vuông góc với mặt phẳng (a). Có bao nhiêu mặt phẳng chứa a và vuông góc với (a) ?
A. 2.
B. 0 .
C. Vô số.
D. 1.
Câu 10. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau đây?
i) Hình hộp đứng có đáy là hình vuông là hình lập phương
ii) Hình hộp chữ nhật có tất cả các mặt là hình chữ nhật
iii) Hình lăng trụ đứng có các cạnh bên vuông góc với đáy
iv) Hình hộp có tất cả các cạnh bằng nhau là hình lập phương
A. 1.
B. 2 .
C. 3 .
D. 4 .
Câu 11. Trong không gian cho hai đường thẳng a, b và mặt phẳng (P), xét các phát biểu sau:
(I). Nếu a // b mà a ^ (P) thì luôn có b ^ (P).
(II). Nếu a ^ (P) và a ^ b thì luôn có b // (P).
(III). Qua đường thẳng a chỉ có duy nhất một mặt phẳng (Q) vuông góc với mặt phẳng (P).
(IV). Qua đường thẳng a luôn có vô số mặt phẳng (Q) vuông góc với mặt phẳng (P). Số khẳng định đúng trong các phát biểu trên là:
A. 1.
B. 4.
C. 2.
D. 3.
Câu 12. Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì cũng vuông góc với đường thẳng còn lại.
C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
D. Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng thì song song với nhau.
Câu 13. Cho hai mặt phẳng (P) và (Q) song song với nhau và một điểm M không thuộc (P) và (Q). Qua M có bao nhiêu mặt phẳng vuông góc với (P) và (Q) .
A. 3 .
B. Vô số.
C. 1.
D. 2.
Dạng 2. Xác định quan hệ vuông góc giữa hai mặt phẳng, mặt phẳng với đường thẳng, đường thẳng với đường thẳng
Dạng 2.1 Đường thẳng vuông góc với mặt phẳng, đường thẳng vuông góc với đường thẳng
Câu 14. Cho hình chóp S.ABCD đều. Gọi H là trung điểm của cạnh AC. Tìm mệnh đề sai?
A. (SAC) ^ ( SBD).
B. SH ^ ( ABCD).
C. (SBD) ^ ( ABCD) .
D. CD ^ ( SAD).
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và SA = SC, SB = SD. Mệnh đề nào sau đây sai?
A. SC ^ (SBD) .
B. SO ^ (ABCD).
C. (SBD) ^ (ABCD) .
D. (SAC) ^ (ABCD) .
Câu 16. Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B và cạnh bên SA vuông góc với mặt phẳng (ABC). Mệnh đề nào sau đây sai?
A. SA ^ BC.
B. AB ^ BC.
C. AB ^ SC.
D. SB ^ BC.
Câu 17. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính sin của góc tạo bởi đường MD và mặt phẳng (SBC) .
A. \[\frac{{\sqrt {13} }}{5}\].
B. \[\frac{{\sqrt {13} }}{3}\].
C. \[\frac{{\sqrt {15} }}{5}\].
D. \[\frac{{\sqrt {15} }}{3}\].
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hai mặt bên (SAB) và (SAD) vuông góc với mặt đáy. AH, AK lần lượt là đường cao của tam giác SAB, SAD. Mệnh đề nào sau đây là sai?
A. BC ^ AH.
B. SA ^ AC.
C. HK ^ SC.
D. AK ^ BD.
Dạng 2.2 Hai mặt phẳng vuông góc
Câu 19. Cho hình chóp S.ABCD có đáy ABCD là hình thoi và SB vuông góc với mặt phẳng (ABCD) . Mặt phẳng nào sau đây vuông góc với mặt phẳng (SBD) ?
A. (SBC).
B. (SAD).
C. (SCD).
D. (SAC).
Câu 20. Cho lăng trụ đứng ABC.A¢B¢C¢ có đáy là tam giác ABC vuông cân tại A. Gọi M là trung điểm của BC, mệnh đề nào sau đây sai ?
A. (ABB¢) ^ (ACC¢).
B. (AC¢M) ^ (ABC) .
C. (AMC¢) ^ ( BCC¢).
D. (ABC) ^ (ABA¢).
Câu 21. Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, cạnh bên SA vuông góc với đáy, I là trung điểm AC, H là hình chiếu của I lên SC. Khẳng định nào sau đây đúng?
A. (BIH) ^ (SBC) .
B. (SAC) ^ (SAB) .
C. (SBC) ^ (ABC).
D. (SAC) ^ (SBC) .
Câu 22. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA ^ (ABC), gọi M là trung điểm của AC. Mệnh đề nào sai ?
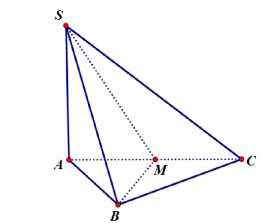
A. (SAB) ^ (SAC).
B. BM ^ AC.
C. (SBM) ^ (SAC).
D. (SAB) ^ (SBC).
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O, SA ^ ( ABCD), SA = \[a\sqrt 6 \] (như hình vẽ). Mệnh đề nào sau đây là đúng?.
A. (SBC) ^ (ABCD).
B. (SBC) ^ (SCD).
C. (SBC) ^ (SAD).
D. (SBC) ^ (SAB) .
Câu 24. Cho hình lăng trụ tứ giác đều ABCD. A’B’C’D’. Mặt phẳng (AB’C) vuông góc với mặt phẳng nào sau đây?
A. (D’BC).
B. (B’BD).
C. (D’AB) .
D. (BA’C’).
Câu 25. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, cạnh bên SA vuông góc với (ABC). Gọi I là trung điểm cạnh AC, H là hình chiếu của I trên SC. Khẳng định nào sau đây đúng?
A. (SBC) ^ (IHB) .
B. (SAC) ^ (SAB).
C. (SAC) ^ (SBC).
D. (SBC) ^ (SAB).
Câu 26. Cho hình chóp S.ABCD có SA ^ (ABCD), đáy ABCD là hình thang vuông tại A và D. Biết SA = AD = DC = a, AB = 2a. Khẳng định nào sau đây sai?
A. (SBD) ^ (SAC).
B. (SAB) ^ (SAD).
C. (SAC) ^ (SBC).
D. (SAD) ^ (SCD).
Câu 27. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy.Trong số các mặt phẳng chứa mặt đáy và các mặt bên của hình chóp, có bao nhiêu mặt phẳng vuông góc với mặt phẳng (SAB) ?
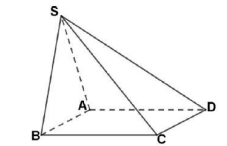
A. 4 .
B. 3 .
C. 1.
D. 2 .
Câu 28. Cho hình hộp ABCD.A¢B¢C¢D¢, khẳng định nào đúng về hai mặt phẳng (A¢BD) và (CB¢D¢).
A. (A¢BD) ^ (CB¢D¢).
B. (A¢BD) // (CB¢D¢).
C. (A¢BD) º (CB¢D¢) .
D. ( A¢BD) Ç (CB¢D¢) = BD¢.
Câu 29. Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA = SC. Khẳng định nào sau đây đúng?
A. Mặt phẳng (SBD) vuông góc với mặt phẳng (ABCD).
B. Mặt phẳng (SBC) vuông góc với mặt phẳng (ABCD).
C. Mặt phẳng (SAD) vuông góc với mặt phẳng (ABCD).
D. Mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD).
Dạng 3. Xác định góc giữa hai mặt phẳng
Dạng 3.1 Góc của mặt phẳng bên với mặt phẳng đáy
Câu 30. Cho hình lập phương ABCD. A¢B¢C¢D¢. Tính góc giữa mặt phẳng (ABCD) và ( ACC¢A¢).
A. 45°.
B. 60°.
C. 30°.
D. 90°.
Câu 31. Cho hình lập phương ABCD. A¢B¢C¢D¢. Góc giữa (ABCD) và (A¢B¢C¢D¢) bằng
A. 45°.
B. 60°.
C. 0°.
D. 90°.
Câu 32. Cho hình chóp tứ giác đều có cạnh đáy bằng \[a\sqrt 2 \]và chiều cao bằng \[\frac{{a\sqrt 2 }}{2}\]. Tang của góc giữa mặt bên và mặt đáy bằng:
A. 1.
B. \[\frac{1}{{\sqrt 3 }}\].
C. \[\sqrt 3 \].
D. \[\frac{3}{4}\].
Câu 33. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt đáy (tham khảo hình vẽ bên). Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng
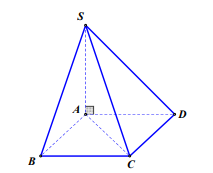
A. Góc \[\widehat {SDA}\].
B. Góc \[\widehat {SCA}\].
C. Góc \[\widehat {SCB}\].
D. Góc \[\widehat {ASD}\].
Câu 34. Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = 4a, AD = = 3a. Các cạnh bên đều có độ dài 5a. Tính góc a giữa (SBC) và (ABCD) .
A. a » 75°46¢.
B. a » 71°21¢.
C. a » 68°31¢.
D. a » 65°21¢.
Xem thêm